Appendix J: Estimation of Impacts
Appendix J_Estimation of Impacts.docx
Program Evaluation of the Partnership for International Research and Education (PIRE) Program
Appendix J: Estimation of Impacts
OMB: 3145-0236
Appendix J: Estimation of Impacts
The following research question will be addressed using a quasi-experimental comparative analysis approach:
RQ 4. How do the research and educational or career outcomes for PIRE PIs, postdoctoral researchers, and graduate student participants compare to those of similar participant groups in similar NSF-funded projects that do not require an international collaboration?
To examine how the research, educational and career outcomes of PIRE participants compare to participants in other NSF-funded projects, the evaluation will match three groups of PIRE participants (PIs, postdoctoral researchers, and graduate students) to corresponding participants from a comparison group of non-PIRE, NSF-funded projects using the approach described in Appendix I: Approach to Matching. The evaluation will also incorporate a comparative interrupted time series (CITS) design for analysis within the matched groups. The reasons for adopting this analytical approach are discussed below.
Rationale for the Evaluation Design
This research design was selected after a determination that neither a randomized control trial, nor a regression discontinuity (RD) design was feasible. Because the PIRE program makes awards on the basis of merit, it was not feasible to randomly assign some PIRE proposals to “award” status (i.e., a treatment group) and others to a “non-award” status (i.e., a control group). Moreover, award decisions for past cohorts of the program had already been made when the evaluation was planned. Although a regression discontinuity design was contemplated, PIRE proposals do not receive a continuous score that is compared to an exogenous “cutoff” to make funding decisions, a key requirement for an RD design. Rather, each proposal receives three or more categorical scores from one (lower merit) to five (highest merit); subsequently, panelists discuss the rated proposals and place each into one of three categories (highly competitive, competitive or not competitive). From these categories, NSF program officers select which proposals to fund, often taking into account additional factors such as geographic and disciplinary variation across the portfolio of funded projects, the institution of the lead PI (e.g., institutions in EPSCOR states).
Another potential quasi-experimental design (i.e., other than an RD design) was also deemed inappropriate, namely a design where unfunded PIRE proposals were matched to funded PIRE projects using propensity score matching (PSM) techniques to control for selection bias. For the evaluation of the PIRE program, this method was not feasible. PSM techniques require data on a large number of pre-treatment (in this case, pre-PIRE award) characteristics of the members of the treatment and comparison groups to model selection and develop propensity scores. Data on pre-award characteristics for funded and unfunded PIRE proposals is limited. Moreover, for the PIRE program, however, it is far from clear what measures at the project level exist for project characteristics before the award decision is made – the project does not exist as a measurable entity until the award decision has been made. For example, the PIRE award itself could affect which individuals come together to form the research group that ultimately engages in research, produces publications, and collaborates with foreign partners. In the absence of the PIRE funding, those individuals did not exist as an already established group for which characteristics can be measured. At the participant level also, it is unclear what group of individuals would form the counterfactual for an unfunded PIRE proposal: without PIRE funding, what individual postdoctoral fellows, graduate students, or undergraduate students could be identified as those who “would have participated” in PIRE and could therefore comprise a valid comparison group? After considering the above evaluation designs, the current approach was adopted as the most feasible design.
Comparative Interrupted Time-Series Analysis
There are three “short” interrupted time-series analysis models we can consider using to measure impacts: (1) a non-linear baseline model, (2) a linear baseline model, and (3) a baseline mean model. We propose to use the baseline mean model1 because it is the simplest and least risky of the three models; it uses five years of pre-treatment data, which makes the mean level more precise than use of only one year of baseline data. Also, this model does not use limited information about changes in performance over time to compute a constant slope (as in linear models) or a time-varying slope (as in nonlinear models) so it avoids the especially large errors that can occur in later follow-up years if one attempts to estimate based on a slope and “guesses wrong” (Bloom, 2003). The interrupted time series model takes the form:

Where:
|
= |
outcome measure for participant k in year j |
|
= |
one if participant k is a PIRE participant and 0 if participant k is a comparison participant |
|
= |
one if year j is after participant k started to participate in the PIRE program; and 0 otherwise |
|
= |
one if participant belongs to the 1st matched group of participants, and 0 otherwise |
… |
|
… additional dummies for additional matched groups |
|
= |
one if participant belongs to the (m-1) matched group of participants, and 0 otherwise (the dummy for the Mth matched group of participants is omitted from the model) |
|
= |
kth participant covariate |
Interpretation of the coefficients in the model is as follows: |
||
|
= |
mean for comparison participants in pre PIRE years |
|
= |
mean for PIRE participants in pre PIRE years |
|
= |
average difference between pre PIRE mean of PIRE participants and comparison participants |
|
= |
comparison participant difference between means of pre PIRE years and means of post PIRE years |
|
= |
PIRE participant difference between means of pre PIRE years and means of post PIRE years |
|
= |
IMPACT (the
effect of PIRE) = ( |
|
= |
A random intercept for participant k
where
|
|
= |
The usual error participant-year specific error term |
Descriptive Relational Analyses
The second and forth research questions require descriptive relational analyses.
RQ 2. How does the quantity and quality of publications produced by PIRE projects—that are required, by definition, to include an international collaboration—compare to the quantity and quality of publications produced by similar NSF-funded projects that do not require an international collaboration?
RQ 4. How do the research and educational or career outcomes for PIRE PIs, postdoctoral researchers, and graduate student participants compare to those of similar participant groups in similar NSF-funded projects that do not require an international collaboration?
The specific approaches that will used to address each of these questions are described below.
2. How does the quantity and quality of publications produced by PIRE projects compare to the quantity and quality of publications produced by similar NSF-funded projects?
OLS regression models will be used to investigate how research outcomes for PIRE projects differ from those of similar NSF projects. Regression models will be fit to data in which the outcomes (e.g. number of publications that are in press, under review, or in preparation) are dependent variables and the independent variables include a dichotomous PIRE indicator (1=PIRE project, 0=comparison project), covariates to control for differences in project level characteristics (e.g., award cohort, duration, funding amount), and variables that indicate matched pairs or matched groups (if we use many-to-one matching). Results will be presented as tables showing the coefficients on the PIRE indicator, as well as any coefficients on covariates.
The coefficient on the PIRE treatment indicator represents the unique relationship of PIRE to differences in number of publications (or another outcome) controlling for other factors included in the model. We will also present descriptive tables that show means, percentages for the outcomes overall, for field of discipline, and for other major subgroups of interest.
4. How do the research educational and career outcomes for PIRE PIs and postdoctoral and graduate student participants compare to those of similar participant groups in similar NSF-funded projects?
The study will compare employment indicators (career outcomes) of PIRE participants against a matched comparison group of participants. This comparison will use relational analyses with controls for characteristics that could be correlated with outcomes.
To address the relational questions, we will fit models of the form shown below:
For research question 2
Project level:

Where:
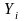 =
outcome measure (e.g. number of publications that are in press) for
the
=
outcome measure (e.g. number of publications that are in press) for
the
 project;
project;
 =
1 if the
=
1 if the
 project is PIRE project and 0 otherwise;
project is PIRE project and 0 otherwise;
 =
1 if project belongs to the 1st matched group and 0 otherwise;
=
1 if project belongs to the 1st matched group and 0 otherwise;
… =…additional dummies for additional matched groups;
 = 1 if project belongs to the (m-1)st
matched group and 0 otherwise (The dummy for the mth
matched group is omitted from the model);
= 1 if project belongs to the (m-1)st
matched group and 0 otherwise (The dummy for the mth
matched group is omitted from the model);
Interpretation of the coefficients in the model is as follows:
 =
covariate adjusted mean value of the outcome for the comparison
projects in the mth matched group;
=
covariate adjusted mean value of the outcome for the comparison
projects in the mth matched group;
 =
is the mean difference in the outcome between matched PIRE and
Comparison projects;
=
is the mean difference in the outcome between matched PIRE and
Comparison projects;
 =
residual error term for the ith project.
The assumed distribution of these residuals is normal, with a mean
of zero and variance of
σ2.
=
residual error term for the ith project.
The assumed distribution of these residuals is normal, with a mean
of zero and variance of
σ2.
For research question 4
 where:
where:
 =
outcome measure for the ith participant
on the jth project;
=
outcome measure for the ith participant
on the jth project;
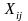 =
one if participant i is a PIRE
participant and 0 if participant i is a
comparison participant;
=
one if participant i is a PIRE
participant and 0 if participant i is a
comparison participant;
 =
pre-publication quality measure for the ith
participant on the jth project;
=
pre-publication quality measure for the ith
participant on the jth project;
 =
pre-publication quantity measure for the ith
participant on the jth project;
=
pre-publication quantity measure for the ith
participant on the jth project;
 =
1 if participant belongs to the 1st matched group of
participants and 0 otherwise;
=
1 if participant belongs to the 1st matched group of
participants and 0 otherwise;
 =
1 if participant belongs to the
=
1 if participant belongs to the
 matched group of participants and 0 otherwise (the dummy for the
matched group of participants and 0 otherwise (the dummy for the
 matched group is omitted from the model);
matched group is omitted from the model);
 =
value of the kth covariate (k=2,…,K) for the ith
participant on the jth project, centered
at the grand mean;
=
value of the kth covariate (k=2,…,K) for the ith
participant on the jth project, centered
at the grand mean;
Interpretation of the coefficients in the model is as follows:
β0j = covariate adjusted mean value of the outcome for the comparison participants
in the mth matched group;
β1j = is the mean difference in the outcome between PIRE and Comparison participants;
β2j … βKj = regression coefficients indicating the effect of each participant-level covariate;
 =
residual error term for the ith
participant on the jth project;
=
residual error term for the ith
participant on the jth project;
The assumed distribution of these residuals is normal, with a mean
of zero and variance of .
.
Model Selection Process
Control variables will be added to the models described above only to help with cofounding and to explain covariance. A brief outline of the model selection process follows.
The first step will be to identify the set of control variables that have statistically significant associations with the outcome (p<0.20 criterion) after controlling for other statistically significant control variables and each predictor variable in the model.2 This will be accomplished using backwards elimination with forward checking. In this method, all of the control variables and each predictor variable are entered as predictors in the model. The control variable with the largest non-significant value will be dropped from the subsequent model. This step is repeated until the only control variables that remain in the model meet the p<0.20 criterion. In the forwards checking step, each of the previously eliminated control variables are checked by adding each one to the model with only the significant predictors. In this step, each variable has a chance to get back into the model.
After selecting the model with significant control variables, the predictor variable will be assessed. Thus, the relationship of each of the predictor variable with the outcome measure is assessed after controlling for the specified control variables. No attempt will be made to fit models with multiple predictors. Each predictor variable is assessed in a model that has only that single predictor, plus the controls.
Please also note that some control variables (e.g. discipline) will be included in the model regardless of significance because of theoretical the relationship (correlation) with the outcome of interest.
1 We will check to see if the baseline mean model is the appropriate model to use by testing whether or not the baseline slope is different than zero. If there is no significant linear trend the baseline mean model is appropriate to use. If there is a significant linear trend we will use either the non-linear or the linear baseline model to estimate impacts.
2 Backwards elimination methods are attractive from the point of view that they are often used and familiar. But use of this method using the conventional p<0.05 criterion has been criticized from the point of view that the selection criteria tends to favor covariates with strong relationships to the outcome, but may omit important confounders (i.e., variables that have a weaker relationship to the outcome, but have a strong relationship to the predictor variable of interest). Maldonado and Greenland (1993) evaluated a backwards elimination strategy and a change-in-estimate strategy using simulated data from a Poisson regression model. They found that the p-value based method performed adequately when the alpha levels were higher than conventional levels (0.20 or more), and found that the change-in-estimate strategy performed adequately when the cut point was set to 10 percent. However, their data, generated from a Poisson model, and their analysis model, with only a single covariate in addition to the key exposure variable, are very different than the models anticipated for our current purpose. Budtz-Jorgensen et al. (2001) compared several covariate selection strategies including backwards elimination and change-in estimate. They looked at the backwards elimination strategy with three p-value cut-off levels, 0.05, 0.10, and 0.20, and, following the recommendation of Maldonado and Greenland (1993) used a 10% criterion for the change-in-estimate method. They found that, although the change-in-estimate strategy did an adequate job of identifying confounders and keeping them in the model, it sometimes threw out variables that were correlated with the outcome, but were not confounders. Therefore, this method threw out variables that, if retained, would have reduced the residual error and reduced the standard error of the exposure coefficient (thus increasing the power to detect exposure effects – exposure effect is analogous to our key predictor of interest). Although they found that backwards elimination with a p<0.05 criterion was un-suited for confounder identification, they found that when the p value criterion was set to p<0.20, backwards elimination strategy resulted in a reduction of residual error variance and did not throw out important confounders. They recommended the backwards elimination strategy with a p<0.20 criterion over the change-in-estimate strategy. See Maldonado, G., Greenland, S., (1993). Simulation study of confounder-selection strategies. American Journal of Epidemiology 138: 923-936; Budtz-Jorgensen, E., Keilding, N., Grandjean, P., Weihe, P.,White, R. (2001). Confounder identification in environmental epidemiology. Assessment of health effects of prenatal mercury exposure. Downloaded from http://www.pubhealth.ku.dk/bsa/research-reports/paper_ms.ps
Appendix
J: Estimation of Impacts
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Title | Abt Single-Sided Body Template |
| Author | Jinyu Luan |
| File Modified | 0000-00-00 |
| File Created | 2021-01-27 |
© 2026 OMB.report | Privacy Policy








 )
)
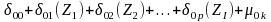
 is normally distributed with a mean 0 and standard deviation
is normally distributed with a mean 0 and standard deviation

