2007 Supporting_Statement_Part_B_Final
2007 Supporting_Statement_Part_B_Final.doc
National Survey on Recreation and the Environment
OMB: 0596-0127
National Survey on Recreation and the Environment (NSRE) 2007
May 2007
![]()
Supporting Statement for OMB 0596-0127
National Survey on Recreation and the Environment (NSRE) 2007
PART B
B. Collections of Information Employing Statistical Methods
1. Describe (including a numerical estimate) the potential respondent universe and any sampling or other respondent selection method to be used. Data on the number of entities (e.g., establishments, State and local government units, households, or persons) in the universe covered by the collection and in the corresponding sample are to be provided in tabular form for the universe as a whole and for each of the strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection had been conducted previously, include the actual response rate achieved during the last collection.
This Information Collection Request (ICR) is for the National Survey on Recreation and the Environment (NSRE). The proponent is requesting approval to survey approximately 55,000 individuals annually, in continuation of the latest in a series of surveys begun in 1960 as the National Recreation Survey (NRS). This request covers versions 4-10 of the survey (versions 1-3 previously approved by OMB, have been completed).
The most recently available Census estimate of the entities to be sampled (2005) shows the number of non-institutionalized persons 16 or older in the U. S. at 231,323,688 (Table 1). The number of households in 2005 was 113,282,551.
The latest collection from this potential respondent universe for the NSRE was conducted between November 2004 and spring 2006. The Standard Random Digit Dial (RDD) sampling applied during this period yielded a raw preliminary response rate from the identified universe of 14.08 percent. An experiment testing response rate effects of pre-notification letters to listed household phones, which had an address with their phone number, yielded an overall response rate of 17.62 percent (combining respondents with and without pre-notification). The experimental pre-notification letters were sent to ½ of the numbers with addresses, while the other ½ was not sent a letter as a test for effects of pre-notification on response rates. On average, 40 percent of numbers list an address. The other 60 percent did not receive pre-notification letters, due to lack of addresses. See Table 2 (below) for final computation of response rates, cooperation rates, refusal rates and contact rates following methods recommended by the American Association of Public Opinion Researchers. Based on these computed response rates, we expect a response rate from an RDD sample of between 16.5 percent and 18.1 percent.
Table 1: Resident Population 16 years and over and total households in 2005
US Population 16+ (1000s) |
# Households (1000s) |
Sample Size Proportional |
Margin of Error |
U. S. (231,324) |
113,283 |
50,000 |
0.004 |
NORTHEAST (43,381) |
20,898 |
9,568 |
0.010 |
New England (11,382) |
5,559 |
2,563 |
0.019 |
Maine (1,082) New Hampshire (1,046 Vermont (509) Massachusetts (5,111) Rhode Island (860) Connecticut (2,775) |
544 506 251 2,505 416 1,337 |
281 236 127 1,131 190 598 |
0.058 0.064 0.087 0.029 0.071 0.040 |
Mid Atlantic (31,999) |
15,399 |
7,005 |
0.012 |
New York (15,235) New Jersey (6,801) Pennsylvania (9,962) |
7,216 3,188 4,934 |
3,313 1,428 2,265 |
0.017 0.026 0.021 |
SOUTH (83,779) |
41,699 |
18,283 |
0.007 |
South Atlantic (44,192) |
22,197 |
9,652 |
0.010 |
Delaware (670) Maryland (4,360) District of Columbia (448) Virginia (5,951) West Virginia (1,480) North Carolina (6,777) South Carolina (3,348) Georgia (6,967) Florida (14,190) |
326 2,100 251 2,951 761 3,502 1,686 3,455 7,166 |
148 925 119 1,253 365 1,520 757 1,416 3,150 |
0.081 0.032 0.090 0.028 0.051 0.025 0.036 0.026 0.017 |
East South Central (13,892) |
7,063 |
3,156 |
0.017 |
Kentucky (3,305) Tennessee (4,733) Alabama (3,595) Mississippi (2,258) |
1,695 2,414 1,842 1,113 |
755 1,052 847 501 |
0.036 0.030 0.034 0.044 |
West South Central (25,695) |
12,439 |
5,475 |
0.013 |
Arkansas (2,182) Louisiana (3,510) Oklahoma (2,793) Texas (17,210) |
1,110 1,740 1,408 8,180 |
506 797 653 3,519 |
0.044 0.035 0.038 0.017 |
MIDWEST (51,734) |
26,252 |
11,632 |
0.009 |
East North Central (36,060) |
18,251 |
8,091 |
0.011 |
Ohio (9,032) Indiana (4,850) Illinois (9,884) Michigan (7,894) Wisconsin (4,401) |
4,654 2,514 4,835 4,004 2,244 |
2,063 1,092 2,108 1,826 1,001 |
0.022 0.030 0.021 0.023 0.031 |
West North Central (15,674) |
8,002 |
3,541 |
0.016 |
Minnesota (4,052) Iowa (2,378) Missouri *4,587) North Dakota (518) South Dakota (611) Nebraska (1,378) Kansas (2,150) |
2,066 1,219 2,330 270 312 707 1,098 |
891 532 1,053 125 139 312 488 |
0.033 0.042 0.030 0.088 0.083 0.055 0.044 |
WEST (52,430) |
24,433 |
10,517 |
0.010 |
Mountain (15,562) |
7,650 |
3,252 |
0.017 |
Montana (758) Idaho (1,098) Wyoming (410) Colorado (3,612) New Mexico (1,498) Arizona (4,525) UTA (1,803) Nevada (1,858) |
372 530 204 1,883 728 2,210 797 925 |
178 228 97 780 337 944 332 357 |
0.073 0.065 0.100 0.035 0.053 0.032 0.054 0.052 |
Pacific (36,868) |
16,783 |
7,265 |
0.011 |
Washington (4,980) Oregon (2,890) California (27,491) Alaska (498) Hawaii (1,008) |
2,457 1,431 12,232 233 430 |
1,057 627 5,269 113 199 |
0.030 0.039 0.014 0.092 0.069 |
Source: U.S. Census Bureau, Census Estimates 2005 - 2005 households--also called occupied housing units--are estimated by multiplying the 2005 estimate of total housing units times the state proportion of occupied housing units in the 2000 Census.
The pre-notification experiment addressed two questions and was applied to versions 1 and 2 conducted from November 2004 to spring 2006 (10,000 respondents overall). The first question was, “Were response rates among households with mailing addresses significantly greater with pre-notification than without?” The answer to this first question based on analysis of the experimental data was “yes.” (See report authored by Leeworthy, et al, as sent to OMB in December 2006, reference cited in Part A of this submission.)
The second question was, “Does pre-notification reduce non-response bias in estimates of the primary study variables, that is, estimates of rates of population participation in recreational activities?” The answer to this second question was “no.”
Pre-notification letters strongly tended to introduce additional bias. People with listed addresses were different in demographics and activity participation then people without listed addresses. Over-representation of pre-notified households with addresses accentuated the bias effects of these differences. Avoiding overrepresentation of any particular segments of a population is one of the primary justifications given for following an RDD design. The verbatim wording of the conclusion from the NSRE pre-notification experiment was:
“Pre-notification letters and refusal letters increase response rates, but they yield samples that are more unrepresentative (of the sampled universe) than Standard RDD. This results in significant biases in (estimates of) activity participation rates. Thus, at any cost, pre-notification and refusal letters do not pass a benefit-cost test if the objective is to reduce non response bias.”
The conclusion drawn is that pre-notification should not be used in future NSRE sampling. Thus, the expected response rates using standard AAPOR approaches for computing RDD response rates will be between 16.5 percent and 18.1 percent (Table 2).
-
Table 2 - Response Rates for NSRE 2005
Version 1 and 2
Response Rate 1 I/(I+P) + (R+NC+O) + (UH+UO)
0.164969
Response Rate 2 (I+P)/(I+P) + (R+NC+O) + (UH+UO)
0.169321
Response Rate 3 I/((I+P) + (R+NC+O) + e(UH+UO) )
0.176167
Response Rate 4 (I+P)/((I+P) + (R+NC+O) + e(UH+UO) )
0.180815
Cooperation Rate 1 I/(I+P)+R+O)
0.223518
Cooperation Rate 2 (I+P)/((I+P)+R+0))
0.229415
Cooperation Rate 3 I/((I+P)+R))
0.241673
Cooperation Rate 4 (I+P)/((I+P)+R))
0.248050
Refusal Rate 1 R/((I+P)+(R+NC+O) + UH + UO))
0.513288
Refusal Rate 2 R/((I+P)+(R+NC+O) + e(UH + UO))
0.548132
Refusal Rate 3 R/((I+P)+(R+NC+O))
0.586596
Contact Rate 1 (I+P)+R+O / (I+P)+R+O+NC+ (UH + UO)
0.738055
Contact Rate 2 (I+P)+R+O / (I+P)+R+O+NC + e(UH+UO)
0.788157
Contact Rate 3 (I+P)+R+O / (I+P)+R+O+NC
0.843464
I = Complete interview; P = Partial interview; R = Refusal and break-off; NC = Non-contact; O = Other; UH = Unknown if household/occupied HU; UO = Unknown, other; e = Estimated proportion of cases of unknown eligibility that are eligible.
Source: The American Association for Public Opinion Research, 2004, Standard Definitions: Final Dispositions of Case Codes and Outcome Rates for Surveys. 3rd ed. Lenexa, KS: AAPOR.
Describe the procedures for the collection of information including:
Statistical methodology for stratification and sample selection: Sampling will be strictly a proportional RDD approach that will represent the spatial distribution of households with phones among regions, states, counties and area codes. No intentional over sampling of areas or population strata will occur. The target will be a random sample of the resident population of individuals 16 years of age or older residing in the United States and the District of Columbia. Households with phones will be selected by means of Random Digit Dialing (RDD), yielding a natural stratification of the sample by state, county, and area code (Frey, 1989; Groves and Kahn, 1979). RDD samples theoretically provide an equal probability of reaching all households in the nation with a telephone access line (i.e., a unique telephone number that rings in that household only), regardless of whether that phone number is published or unlisted (Lavrakas, 1987).
The RDD sampling frame produces proportionate stratified random samples from working blocks of phone numbers from Central Office Exchanges (COEs) located within specified geographic boundaries. The sample is first systematically stratified to all U.S. counties in proportion to each county’s share of telephone households. The total of telephone households is calculated and divided by the desired sample size to produce the sampling interval. Counties are then ordered alphabetically by state and county within state, a random number between one and the sampling interval is generated, and a cumulative count of telephone households is generated. At the point where the count reaches the random starting point, a specific county is selected. The second element selected is one interval away from the first point. Counties whose population is greater than the sampling interval are selected repeatedly and counties where the population is less than the interval have some chance of being skipped. Thus, the sampled households with a telephone are distributed across counties in proportion to their share of the total population of telephone households.
A second level of stratification occurs when specific blocks of numbers within a county are selected. From a random start within the first sampling interval, one or more blocks of numbers are selected systematically. A second sampling interval is then calculated by summing the number of listed residential numbers in each working block and dividing the sum by the desired quantity of elements. Thus, each block’s chance of being selected is proportional to its share of listed households, such that the more active blocks of numbers have a greater probability of selection. These methods of stratification equalize the probability of selection for all U.S. telephone households and the resulting sample is self-weighting. No intentional disproportionate sampling will be conducted.
Once random generated numbers are contacted, eligible respondents will be selected within households by means of a “last birthday” technique. The selected respondent will be the household member 16 years of age or older who last had a birthday. The interviewer inquires how many people in the household are 16 years or older, then asks to speak to the person with the most recent birthday (Oldendick, Bishop, Sorenson & Tuchfarber, 1988). This method of selection is a probability technique based on the premise that the date of a birthday relative to the date on which an interview is requested provides random selection (Salmon and Nichols, 1983), and does not require an enumeration of household members. The technique has the additional advantages of being less threatening (Frey, 1989), provides an equal chance of selection and helps eliminate any bias toward selection of older respondents (Salmon and Nichols, 1983). Moreover, experimental comparisons (O’Rourke and Blair, 1983) of the “last birthday” method with more elaborate selection procedures (i.e., Kish), find no significant differences in representativeness, and report higher cooperation rates with the “last birthday” method (Frey, 1989).)
Estimation procedure: Estimates of the number of entities (i.e., size of the U.S. non-institutionalized resident population 16 years of age or older) by states and regions were presented in Table 1 (column 1). This table also presented estimated number of households (column 2), and estimated sample sizes for each state and region (column 3). Column 4 of Table 1 reported the estimated theoretical margins of error associated with the proposed state, regional, and national sample sizes assuming a population proportion (P) of 50 percent (i.e., a “worst case scenario”). Table 3 reports the theoretical standard errors and margins of errors for the state and regional samples for various values of P (proportion) and of n (random sample size). The standard errors are derived from the mathematical formula:
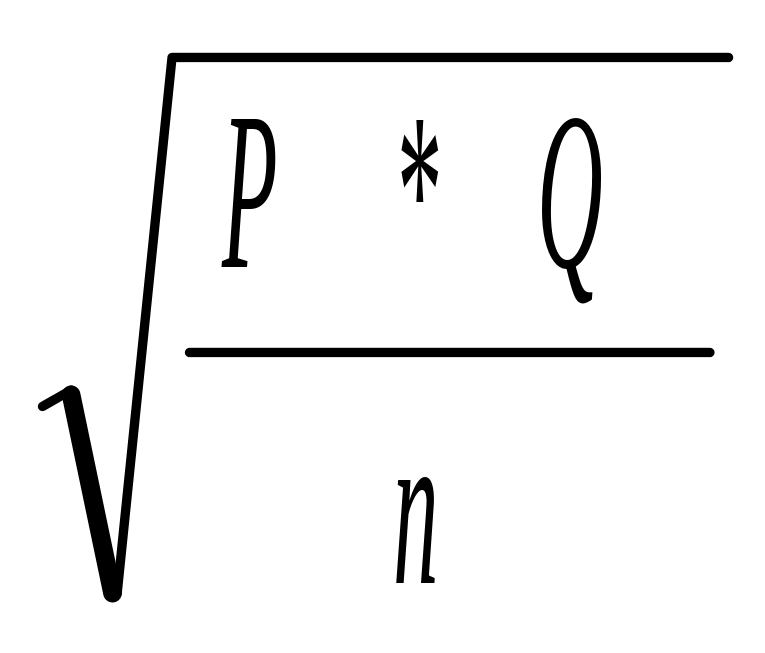
Where: P = the proportion of the population exhibiting a characteristic (e.g., playing golf); Q = (1 - P), the proportion not exhibiting the characteristic; n = size of the sample.
Once obtained, the standard errors can be used to estimate the margin of error of the estimates that extend 1.96 standard error units (i.e., the 95% confidence interval) around the estimates, i.e., P +/- 1.96 * (standard error).
Thus, for example, with a sample size of 10,517 (i.e., the sample for the West Region) and a population proportion of 30 percent, the 95% confidence interval for the estimate would be: .30 +/- 1.96 * .0046 = .30 +/- 0.009 = 30% +/- 0.9% = 29.1% to 30.9%.
Using a formula suggested by Lavrakas (1986), the size of the sampling pool for the proposed study is:
Size of Sampling Pool = Number of interviews to be Completed
[HR] * [1 - REC] * [1 - LE]
= 50,000
.25 * .95 * .50
= 50,000
.11875
= 421,053
Where: HR = estimate of proportion of RDD numbers attached to working phones that will ring at appropriate households;
REC= proportion of respondents determined ineligible due to relational criteria (e.g., no one in household over age 16);
LE = loss of eligible respondents due to refusal, inability to schedule, etc.
In an attempt to provide a more conservative estimate of the required size of the sampling pool of telephone numbers, the estimate is arbitrarily inflated by 10 percent, producing a final sampling pool of 463,158 potential sampling elements or telephone numbers.
Table 3: Theoretical Standard Errors and Confidence Intervals for Various Sample sizes and Population Proportions
50% 30% 10%
SAMPLE SIZE STD ERR 95% CI STD ERR 95% CI STD ERR 95% CI
50,000 .0022 (.0044) .0020 (.0040) .0013 (.0026)
40,000 .0025 (.0049) .0023 (.0045) .0015 (.0029)
25,500 .0031 (.0061) .0028 (.0056) .0018 (.0036)
17,500 .0038 (.0074) .0035 (.0068) .0023 (.0044)
15,000 .0041 (.0080) .0037 (.0073) .0024 (.0048)
12,500 .0045 (.0088) .0041 (.0080) .0027 (.0053)
10,000 .0050 (.0100) .0046 (.0090) .0030 (.0059)
7,500 .0058 (.0113) .0053 (.0104) .0035 (.0068)
5,000 .0070 (.0139) .0065 (.0127) .0042 (.0083)
4,500 .0074 (.0146) .0068 (.0134) .0045 (.0088)
4,000 .0079 (.0155) .0072 (.0142) .0047 (.0093)
3,500 .0084 (.0166) .0077 (.0152) .0051 (.0099)
3,000 .0091 (.0179) .0092 (.0180) .0055 (.0107)
2,500 .0100 (.0196) .0091 (.0179) .0060 (.0117)
2,000 .0111 (.0217) .0102 (.0200) .0067 (.0131)
1,500 .0129 (.0252) .0118 (.0231) .0077 (.0151)
1,000 .0158 (.0310) .0145 (.0284) .0095 (.0186)
500 .0223 (.0437) .0204 (.0401) .0134 (.0262)
100 .0500 (.0980) .0458 (.0898) .0300 (.0588)
Degree of accuracy needed for the purpose described in the justification:
+ 3 % at 95% CI (See Table 3)
Unusual problems requiring specialized sampling procedures:
There are no unusual problems requiring specialized sampling procedures
Any use of periodic (less frequent than annual) data collection cycles to reduce burden.
No special cycles will be needed to reduce burden. Households are sampled only once throughout the survey cycle.
3. Describe methods to maximize response rates and to deal with issues of non-response. The accuracy and reliability of information collected must be shown to be adequate for intended uses. For collections based on sampling, a special justification must be provided for any collection that will not yield "reliable" data that can be generalized to the universe studied.
NASS Statistics Review: The USDA National Agricultural Statistical Service (NASS) reviewed the statistical methodology and design for generating appropriate response rates for the NSRE.
The Agency’s assessment was:
Scot Rumburg
USDA/NASS Statistical Methods Branch
202 720-5617
Observations regarding NSRE Survey:
I see no problems with the statistical methodology of this survey. It has been implemented in similar form several times previously so variances and standard error estimates should be good.
The time to complete the first part – Participation and Days - seems a little conservative if I am correct that it runs through the first 337 questions. I realize that not all questions will need to be answered and that the survey instrument will route based on negative/affirmative responses, but just answering no to all questions took me close to 10 minutes. Are some questions not asked for certain regions, samples etc.? If you or your contractor have tested and timed it I’m probably not routing correctly and this can be disregarded. All other times seem reasonable.
Made a few changes/suggestions in red in the statistics section below for what its worth with regards to grammar and typos: 33, 41, 42, and 43”
(Note from NSRE survey team, all versions and modules have been tested for time per respondent and are as shown in Part A. The typographical errors noted in item 3 were corrected.)
General Overview of Methods Used to Maximize Response Rates and Control for Non-Response Bias
Carefully design, test and revise the survey contents
Design of the NSRE phone survey was refined through application to maximize response rates without introducing unnecessary bias. Designers gave careful attention to input received from experienced phone interviewers at the University of Tennessee and elsewhere. Wording assures respondent understanding. Question order eases flow, maximizes and maintains interest in the subject matter, and assuring consistency and validity over time.
A change from previous applications of NSRE is the identification of the NSRE as a government-sponsored survey. Government sponsored surveys have been found to have higher response rates than other surveys. The introduction now reads as follows:
“Hello. My name is ….. and we are calling on behalf of the United States Forest Service and the National Oceanic and Atmospheric Administration (NOAA)…”
Scheduling callbacks
Each eligible number will be attempted a minimum of 15 times at various intervals throughout the day and on different days of the week to maximize the opportunity of interviewing an eligible member of each eligible household. To minimize respondent burden and encourage full involvement in the survey, each person is asked, “Is this a good time to answer a few questions or would another time be better for you?”
The Computer Aided Telephone System (CATI) facilitates the scheduling of callbacks at specific times if requested by the respondent. The computer manages the database of telephone numbers so that scheduled callbacks are distributed to the first available interviewer at the designated time and date. An option of receiving a mailed hard copy of the survey is accommodated if the respondent requests it. Very few requests are made for a mail survey.
Training
Interviewer training is a vital part of achieving maximum response rates. All interviewers undergo intensive and detailed training so that they have a high level of familiarity and have practiced administering the survey. Each interviewer is monitored regularly for quality control purposes and additional training is provided as needed. An area of emphasis in training is approaches for refusal aversion and refusal conversion.
Minimize language barriers
To maximize response rates, the NSRE is also administered in Spanish. Interviewers screen for Spanish-only people at the beginning of the survey. If positive, they are transferred to a Spanish-speaking interviewer.
e. Meet AAPOR quality standards
Similar surveys repeated over a five-year period at the Human Dimensions Research Lab which use the same RDD methods as the NSRE have been shown to produce very reliable results. (See Table 2 for the response, cooperation, contact and refusal rates for versions 1 and 2 of this survey.) Response rates are calculated using alternative methods of calculating response rates as provided by the American Association of Public Opinion Research. The UT Lab follows the code of ethics set by the American Association of Public Opinion Research and constantly works to follow the AAPOR quality standards. Adherence to ethics and quality standards are basic to maintaining response rates and gaining confidence of the interviewee.
f. Attempt to convert refusers
Efforts to convert refusals have been increased by raising the number of call-backs from 8 to 15. As a part of the earlier described experiment using pre-notification, a random sample of immediate (“soft refusals,” including those who hang up immediately) and a sample of those not ever contacted were selected. A portion of these refusers had a mailing address available. Of refusers with addresses, one-half were sent an explanatory letter indicating the nature of the survey and its importance. The letter notified the household that a further callback would be made to solicit their participation in the survey. Their phone numbers were then attempted again. The results of completed surveys from converted refusers who had been sent a letter were compared with the results from those not sent a letter. Refusal letters increased response rates, but they yielded samples that were more unrepresentative than standard or proportional RDD. This results in significant biases in estimated activity participation rates. Thus, use of refusal letters will be discontinued in versions 4 through 10.
g. Weight to correct for over or under representation of population strata
After data collection is complete, demographic characteristics of sample respondents will be compared with the most current estimates of the distribution of population among demographic strata based on the 2000 Census. The U.S. Census Bureau has advised us that the appropriate population for telephone samples is the civilian non-institutionalized population. Update estimates are typically provided in June of each year. This comparison focuses on the non-institutionalized civilian population age 16 or older and looks at proportions of the sample and population by age, sex, race and Hispanic origin. Any necessary corrections based on geographic distribution, ethnicity, sex, and age will be post weighted to align with current estimates of the non-institutionalized civilian population age 16 or older.
Two weighting approaches will be used by each of the two primary sponsors of the NSRE. The Forest Service and its clients will use post-stratification weighting which adjusts proportions of respondents among demographic strata in the sample relative to proportions of the people 16 or older in the U. S., regional or other populations for which estimates are being produced. NOAA will weight using coefficients estimated from logit models run on marine recreation activities. In either case, responses from sampled individuals will be assigned given greater or lesser weight depending on whether they ended up under or over represented in the sample, respectively. The objective would be a collective distribution of respondents across socio-demographic strata that mirror the distribution of the U. S. population and regional populations across the same strata. This is a widely accepted, non-controversial and necessary method for addressing non-response issues.
Simple Post Stratification Weighting -- Post-stratification will used to approximate data that would result from a proportionate sample across demographic strata. Post-stratification adjusts estimates of participation rate means that can be biased because of disproportionate representation of strata, each with a different propensity to participate in different recreational activities, for example, persons 16 to 24 years of age vs. persons over 65. Post-stratification relies on Census estimates of the distribution of the population among demographic strata.
The NSRE post-stratification corrects for the under- or over-representation of social strata in a sample (Zhang 2000, Holt and Smith 1979). Post-stratification has been successfully applied in similar national surveys in other countries (e.g., Thomsen and Halmoy 1998). For NSRE, a total of 60 strata (6 age x 2 sex * 5 race) have been identified to match identical strata in U.S. Census data. Each individual strata weight, SWi, is the ratio of the Census population proportion to the NSRE 2000 sample proportion:
SWi = Pi / pi, where Pi = U.S Census proportion for strata I, pi = NSRE 2000 sample proportion for strata i.
A weight SWi >1.0 indicates that the particular strata is a smaller proportion of the sample (underrepresented) than it is in the Census population data. A weight SWi <1.0 indicates that the strata was randomly sampled in greater numbers (overrepresented) than their proportion of the U.S population. Each individual NSRE respondent belongs to only one of the 60 age*sex*race strata and thus are assigned the SWi for that strata.
An additional weighting step is to account for the sampling proportions of two other socioeconomic strata: educational attainment and place of residence (rural/urban). The education weight, EWi, is the ratio of Census to Sample proportions for 9 different levels of educational attainment, ranging from “8th grade or less” to “Doctorate Degree”. The residence weight, RWi, is the ratio of the percentage of the U.S. population living in metropolitan and non-metro areas divided by the same proportions in the NSRE 2000. A single weight, Wi, for each individual survey respondent was then calculated as the product of the three interim weights:
Wi= SWi * EWi * RWi
Multivariate Model Approach to Weighting: A Generalized Heckman Approach
This approach uses a more generalized Heckman approach (Heckman, 1979). The Heckman approach uses a probit model. Lee (1983) generalized this approach to other forms of estimation such as the binary logit. In our report to OMB on the pre-notification letter requirement (Leeworthy et al, 2006), demographic strata were identified for age, race/ethnicity, education, Census division, urban/rural, and income. Preliminary logit model results are summarized in Table 4. These models are based on analysis of version 1 and 2. Models were developed for walking, bird watching, hunting, fishing, motor boating, swimming in natural bodies of water, family gatherings outdoors, hiking and mountain biking. We found that adjusting for non response bias using simple sample weights for the demographic factors wasn’t sufficient to adjust for non response bias. We propose to use the binary logit selection correction method as found in Green (1995).
Table 4: Estimated Logit participation functions and demographic strata coefficients by activity
|
Activities (Participation Function Coefficients) 1 |
|||||
Factor |
Walk |
Bird |
Hunt |
Fish |
Mboat |
Swim_nat |
Constant |
2.0135 * |
-1.7295 * |
-2.4595 * |
-0.1996 |
-2.2920 * |
-0.3633 |
Age16_24 |
|
|
|
|
|
|
Age25_34 |
-0.4028 * |
0.2950 * |
0.1484 |
-0.1381 |
-0.2859 * |
-0.8554 * |
Age35_44 |
-0.4196 * |
0.6511 * |
0.01750 |
-0.0399 |
-0.2073 |
-0.8776 * |
Age45_54 |
-0.4822 * |
0.9523 * |
-0.3326 * |
-0.3739 * |
-0.4490 * |
-1.2848 * |
Age55_64 |
-0.6961 * |
1.0253 * |
-0.5556 * |
-0.7318 * |
-0.5743 * |
-1.7689 * |
Age65p |
-0.8667 * |
0.8795 * |
-1.2766 * |
-1.1430 * |
-1.0778 * |
-2.6188 * |
Male |
-0.4790 * |
-0.3234 * |
1.9424 * |
0.8941 * |
0.2605 * |
-0.0838 |
White |
0.2184 |
0.3193 |
0.3034 |
-0.2343 |
0.5561 * |
0.01489 |
Black |
0.0136 |
-0.5101 * |
-1.1572 * |
-1.0233* |
-1.0292 * |
-1.5114 * |
Asian |
-0.5876 |
-0.3081 |
-2.1376 * |
-0.6259 * |
-0.5952 |
-1.0633 * |
Native |
|
|
|
|
|
|
Hispan |
0.3984 |
-0.0717 |
-0.2655 |
-0.4910 * |
-0.0695 |
-0.2902 |
Educ11 |
|
|
|
|
|
|
Educhs |
0.0919 |
0.2228 * |
0.0642 |
0.1732 |
0.3356 * |
0.2535 * |
Educcoll |
0.6621 * |
0.5283 * |
-0.3799 * |
-0.1052 |
0.5563 * |
0.7895 * |
Educgrad |
1.1007 * |
0.7098 * |
-0.8481 * |
-0.3349 * |
0.5567 * |
1.0293 * |
Educoth |
0.5216 |
0.6037 * |
0.3276 |
0.0247 |
0.4603 |
0.5477 * |
Inc25 |
|
|
|
|
|
|
Inc50 |
0.4378 * |
0.1548 * |
0.5207 * |
0.2822 * |
0.5972 * |
0.4102 * |
Inc100 |
0.5850 * |
0.1602 * |
0.7252 * |
0.4127 * |
0.9219 * |
0.7177 * |
Inc100p |
0.8502 * |
0.2737 * |
0.4584 * |
0.3627 * |
1.1969 * |
1.0508 * |
Incmiss |
0.1983 * |
-0.04255 |
0.3506 * |
0.1057 |
0.6480 * |
0.3695 * |
Urban |
0.0056 |
-0.1079 * |
-0.9219 * |
-0.3769 * |
-0.05972 |
0.0962 |
Cendiv1 |
-0.1376 |
0.4145 * |
-0.8985 * |
-0.1772 |
0.0721 |
1.1323 * |
Cendiv2 |
-0.3649 * |
0.0564 |
-0.4078 * |
-0.3788 * |
-0.0681 |
0.8177 * |
Cendiv3 |
-0.3902 * |
0.2478 * |
-0.3567 * |
0.2291 * |
0.2390 * |
0.8348 * |
Cendiv4 |
-0.4160 * |
-0.07608 |
-0.0617 |
0.1944 |
0.1345 |
0.1971 |
Cendiv5 |
-0.3848 * |
-0.07841 |
0.4196 * |
0.2287 * |
0.1533 |
0.1306 |
Cendiv6 |
-0.3010 * |
0.1329 |
-0.1956 |
-0.0907 |
0.3018 * |
0.3401 * |
Cendiv7 |
-0.3305 * |
0.1265 |
0.3819 * |
0.3008 * |
0.6234 * |
0.1505 |
Cendiv8 |
|
|
|
|
|
|
Cendiv9 |
-0.0444 |
0.1893 * |
-0.6487 * |
-0.3201 * |
0.0646 |
0.5304 * |
Standrdd |
-0.1161 |
-0.0342 |
0.0496 |
-0.0295 |
-0.0431 |
-0.0823 |
Rfconv |
-0.0120 |
-0.05902 |
0.0952 |
0.0469 |
0.0105 |
0.0268 |
1. *=significance at .05 or less and blank means dummy category in constant. |
||||||
Table 4: Estimated Logit participation functions and demographic strata coefficients by activity
(continued)
|
Activities (Participation Function Coefficients) 1 |
|
|||
Factor |
Fam |
Hike |
Mtnbike |
||
Constant |
1.4254 * |
-0.1291 |
-0.4047 |
||
Age16_24 |
|
|
|
||
Age25_34 |
-0.5042 |
-0.0015 |
-0.2590 |
||
Age35_44 |
-0.3066 |
0.0409 |
-0.5090 * |
||
Age45_54 |
-0.8422 * |
-0.0358 |
-0.8405 * |
||
Age55_64 |
-1.0638 * |
-0.2807 |
-1.3171 * |
||
Age65p |
-1.0568 * |
-0.8734 * |
-2.2554 * |
||
Male |
-0.1919 * |
0.2922 * |
0.5045 * |
||
White |
-0.0603 |
-0.1265 |
-0.4092 |
||
Black |
0.5756 |
-1.5053 * |
-0.7284 * |
||
Asian |
-0.6144 |
-0.7431 |
-1.1048 * |
||
Native |
|
|
|
||
Hispan |
-0.0736 |
-0.3153 |
-0.6593 |
||
Educ11 |
|
|
|
||
Educhs |
0.0311 |
0.0347 |
-0.2303 |
||
Educcoll |
0.3132 |
0.2549 |
0.0179 |
||
Educgrad |
0.2864 |
0.6239 * |
0.2875 |
||
Educoth |
0.5934 |
0.0713 |
0.0161 |
||
Inc25 |
|
|
|
||
Inc50 |
0.2352 |
0.2692 * |
0.1371 |
||
Inc100 |
0.5907 * |
0.4858 * |
0.1431 |
||
Inc100p |
0.5509 * |
0.5160 * |
0.5205 * |
||
Incmiss |
0.1868 |
0.0671 |
-0.1510 |
||
Urban |
-0.2239 |
-0.0160 |
-0.0016 |
||
Cendiv1 |
0.3516 |
-0.6420 * |
0.0255 |
||
Cendiv2 |
0.1869 |
-0.7786 * |
-0.0032 |
||
Cendiv3 |
0.0070 |
-0.9184 * |
-0.0227 |
||
Cendiv4 |
0.1612 |
-1.0940 * |
-0.3645 |
||
Cendiv5 |
0.2237 |
-1.2887 * |
-0.6838 * |
||
Cendiv6 |
0.1661 |
-0.8698 * |
0.1349 |
||
Cendiv7 |
0.1893 |
-0.8318 * |
0.0324 |
||
Cendiv8 |
|
|
|
||
Cendiv9 |
0.4111 |
-0.3019 * |
-0.0192 |
||
Standrdd |
-0.1696 |
-0.0157 |
-0.0127 |
||
Rfconv |
-0.1206 |
-0.0244 |
-0.0793 |
||
1. *=significance at .05 or less and blank means dummy category in constant. |
|||||
To test for the effects of socio-demographic variables on participation rates logit equations were estimated using both the SAS 9.0 software and LIMDEP 7.0. SAS enabled testing the “main effect” for each socio-demographic variable and pairwise comparison. This is analogous to what is usually done in an analysis of variance. The full results are not shown here since they are not central to submission. The results of the logit equations showing main effects of each demographic variable are summarized in Table 5. What this analysis demonstrated was that demographic factors for which there was either under or over representation in our sample, as compared to the Census, were significant factors in explaining participation in outdoor recreation activities and thus non response bias.
Table 5: Tests (P-values) on the Main Effects in the Logit Participation Models Based on the Wald Chi-Square Test
Factor |
Walk |
Bird |
Hunt |
Fish |
Mboat |
Swim_Nat |
Fam |
Hike |
Mtnbike |
Age |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
Gender |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
0.0691 |
0.0424 |
<0.0001 |
<0.0001 |
Ethrace |
0.0019 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
0.0768 |
<0.0001 |
0.0305 |
Educ |
<0.0001 |
<0.0001 |
<0.0001 |
0.0006 |
<0.0001 |
<0.0001 |
0.1182 |
<0.0001 |
0.0026 |
Income |
<0.0001 |
<0.0002 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
0.0012 |
<0.0001 |
<0.0001 |
Urban |
0.9509 |
0.0535 |
<0.0001 |
<0.0001 |
0.3061 |
0.1067 |
0.0624 |
0.8248 |
0.9839 |
Cendiv |
0.0189 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
<0.0001 |
0.4671 |
<0.0001 |
0.0003 |
Standrdd |
0.0818 |
0.4416 |
0.4996 |
0.5189 |
0.3851 |
0.0777 |
0.0805 |
0.7888 |
0.8585 |
Rfcon |
0.8733 |
0.2180 |
0.2235 |
0.3818 |
0.8603 |
0.6294 |
0.2559 |
0.7377 |
0.3900 |
Multivariate weights will be constructed from the logit results for age, gender and race/ethnicity using Census data for the non-institutionalized population 16 years old and older and our sample data. Multiplicative weights for educational attainment and urban/rural residency will be applied. An application of weighting the NSRE versions 1 and 2 data provided comparisons of unweighted and weighted estimates of activity participation rates for the “Full Sample” (Table 6). There were significant differences between the unweighted and weighted estimates for 5 of the 9 activities tested. Unweighted estimates were always higher than weighted estimates indicating a general upward bias in unweighted data. Thus, our conclusion is that this weighting will not be sufficient for adjusting for non response bias, there are factors other than demographic factors we have in the survey that are responsible for non response bias. Therefore, we will implement the binary logit selection correction method for each recreation activity in deriving activity participation rates.
Table 6: Differences in Unweighted and Weighted Estimates of Activity Participation Rates: Full Sample
|
Unweighted |
Weighted |
Statistically Significant |
Sample Group/Activity |
95% C.I.1 |
95% C.I.2 |
Difference3 |
Walking |
0.8723 (0.8658, 0.8788) |
0.8513 (0.8442, 0.8584) |
Yes, + |
Birding |
0.4203 (0.4107, 0.4299) |
0.3450 (0.3358, 0.3542) |
Yes, + |
Hunting |
0.1255 (0.1190, 0.1320) |
0.1191 (0.1128, 0.1254) |
No,+ |
Fishing |
0.3417 (0.3325, 0.3509) |
0.3380 (0.3288, 0.3472) |
No, + |
Motor boat |
0.2880 (0.2792, 0.2968) |
0.2407 (0.2323, 0.2491) |
Yes, + |
Swimming natural water |
0.4532 (0.4434, 0.4630) |
0.4034 (0.3938, 0.4130) |
Yes, + |
Family outing |
0.7237 (0.7059, 0.7415) |
0.7197 (0.7019, 0.7375) |
No, + |
Hiking |
0.3486 (0.3355, 0.3617) |
0.2987 (0.2860, 0.3114) |
Yes, + |
Mountain biking |
0.1972 (0.1862, 0.2082) |
0.1902 (0.1794, 0.2010) |
No, + |
1. 95 percent confidence interval on estimated activity participation rates using unweighted data. |
|||
2. 95 percent confidence interval on estimated activity participation rates using weighted data. |
|||
3. Yes or No for statistically significant difference between unweighted and weighted estimates of activity participation rates; + or - indicating unweighted estimate of activity participation rate is greater (+) or less (-) than the weighted estimate of activity participation rate. |
|||
h. An additional step for identifying and comparing refusers
An additional step taken with regard to non-response adjustment is to include a follow-up to refusals to ask a very limited number of questions (age and participation in walking). A comparison with RDD age and walking participation results will be done to identify potential non-response bias. Analysis of versions 1 and 2 demonstrated that there are differences between those who do and do not respond to the full survey. These differences have been shown to result in non-response bias. Current sample weighting is not accounting for all of this bias. An additional sample weight will be constructed to account for refusals having a higher rate of non-participation in outdoor recreation than those that respond to the full survey.
i. Increase level of detail for recording call dispositions
Keeping more detailed records of residential household status of non-contacted households will enable better estimates the value of “e”, which is the estimated proportion of cases of unknown eligibility that are eligible. “e” is used to calculate AAPOR’s Response Rate 3. In the 2007 NSRE, all no answer and busy signal attempts are reviewed to determine whether the number is residential and if all call attempts resulted in “ring/no answer” or “always busy.” Those calls that are of unknown residential status will be coded as such. A residency rate will be kept to indicating the percentage of numbers of unknown status that are likely to be residential households.
j. Reducing Survey Length
Survey length will be kept to 15 minutes. Thus, all versions of the NSRE will be limited to not more than a 15-minute interview time on average. All versions of the NSRE are submitted to extensive testing and refinement before application, thus the alternative designs will be of known time at implementation. The Human Dimensions Research Lab at The University of Tennessee has shown that response rates improve with shorter interviews.
4. Describe any tests of procedures or methods to be undertaken. Testing is encouraged as an effective means of refining collections of information to minimize burden and improve utility.
The NSRE has been performed over tens of thousands of individual respondents from 1994-1995 and from 1999 to now. Surveying from 2004 to now has been described earlier. In addition, a number of experiments have been performed with results submitted to OMB in December 2006. The report was entitled “Survey Response Rate and Bias Results from a Trial of Pre-notification Letters: A Report to the Office of Management and Budget on the National Survey on Recreation and the Environment (NSRE)” , December 2006. The results of the experimentation performed over versions 1 and 2 have been evaluated and are reflected in this request.
Provide the name and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
Human Dimensions Research Lab, University of Tennessee
Dr. J. Mark Fly, Professor, (865) 974-7979
Ms. Becky Stephens, Sr. Research Associate, (865) 974-5495
April Griffin, Research Technician (865) 974-6864
Misty Gladdish, Lab Supervisor
Tabatha Freeman, Lab Supervisor
Shelby Singleton, Lab Supervisor
Social Science Research Institute, University of Tennessee, subcontractor assisting with data collection
Dr. Michael Gant, Director (865) 974-7541
Ms. Linda Daugherty, Manager (865) 974-2818
Department of Agricultural and Applied Economics, University of Georgia
Dr. John C. Bergstrom, Professor
Warnell School of Forest Resources, University of Georgia
Dr. Michael A. Tarrant, Professor
Southern Research Station, USDA Forest Service
Dr. Michael Bowker, Scientist
Dr. Cassandra Johnson, Scientist
Dr. Stan Zarnoch, Statistical Scientist
National Oceanic and Atmospheric Administration, Washington DC
Dr. Robert Leeworthy, Scientist (301) 713-3000 ext. 138
Literature Cited:
Frey, J. (1989). Survey Research by Telephone. Sage Publications. Thousand Oaks, CA.
Green, W. H. (1995). LIMDEP Version 7.0 User’s Manual, Chapter 28, pp.637-648, Econometric Software, Inc., Bellport, NY.
Heckman, J. (1979). Sample Selection Bias as a Specification Error, Econometrica, 47, pp.153-161.
Holt, D., & Smith, T. M. F. (1979). Post‑stratification. Journal of the Royal Statistical Society, A‑142, 33‑46.
Lee, L. (1983). Generalized Econometric Models with Selectivity, Econometrica, 51, pp. 507-512.
Leeworthy, V.R., Zarnoch, S., Cordell, H.K., Green, G.T., Fly, J.M., and Stephens, R. (2006). Survey Response Rate and Bias Results from a Trial of Pre-notification Letters: A Report to the Office of Management and Budget on the National Survey on Recreation and the Environment (NSRE). Submitted to OMB by the U.S. Forest Service, National Oceanic and Atmospheric Administration, University of Georgia, and University of Tennessee, December 6, 2006.
Lavrakas, P. (1987). Telephone Survey Methods: Sampling, Selection, and Supervision. Sage Publications, Thousand Oaks, CA.
Oldendick, R. W., Bishop, G. F., Sorenson, S. W., & Tuchfarber, A. J. (1988). A comparison of the Kish and Last Birthday Methods of respondent selection in telephone surveys. Journal of Official Statistics, 4, p. 307-318.
O'Rourke, Diane., & Blair, Johnny. (1983). Improving Random Respondent Selection in Telephone Surveys. Journal of Marketing Research (JMR); Nov 83, Vol. 20 Issue 4, p428-432
Salmon, Charles, & Nichols, John. (1983). The Next- Birthday Method of Respondent Selection. Public Opinion Quarterly; Summer 83, Vol. 47 Issue 2, p. 270-7
Thomsen, I., & Halmoy, A. (1998). Combining data from surveys and administrative record systems: The Norwegian experience. International Statistical Review, 66(2), 201‑221.
Zhang, L. C. (2000). Post‑stratification and calibration‑‑A synthesis. American Statistician, M(3), 178-184.
| File Type | application/msword |
| File Title | Supporting Statement for OMB 0596-0127 |
| Author | FSDefaultUser |
| Last Modified By | FSDefaultUser |
| File Modified | 2007-05-17 |
| File Created | 2007-05-10 |
© 2026 OMB.report | Privacy Policy