3060-1265 Administrative Order Performance Testing Measures Statistical Methodology_final version 5.26.22
3060-1265 Administrative Order Performance Testing Measures Statistical Methodology_final version 5.26.22.docx
Administrative Order - Performance Testing Measures
OMB: 3060-1265
Administrative Order – Performance Testing Measures 3060-1265 September 2024
SUPPORTING STATEMENT
Part B: Statistical Methodology
We performed statistical analysis to determine the number of subscriber test locations required for each carrier. In doing so, we balanced the goals of achieving statistically precise estimates (i.e., an understanding of the precision of the test result data) and avoiding unnecessarily burdening respondents.
The goal of the testing is to determine whether carriers are meeting their performance obligations. To demonstrate that a carrier provides broadband Internet service with the required upload or download speeds in a particular state and speed service tier (e.g., 25/3 Mbps or 10/1 Mbps), 80% of the carrier’s test result data points in a state and service tier combination must be at or above 80% of the required speed. Such data points follow a binomial distribution (i.e., an individual test result either is 80% or better or it is not). For a binomial distribution, the number of samples n required to achieve the target confidence level in the worst-case scenario can be calculated with the following equation:

where
 is the z-score of the
is the z-score of the
 th
percentile of the normal distribution, and MOE represents the margin
of error, which is half the width of the desired confidence interval.
th
percentile of the normal distribution, and MOE represents the margin
of error, which is half the width of the desired confidence interval.
The following Finite Population Correction equation calculates the corrected sample size nd when performing sampling without replacement from a finite population N, to achieve an estimate with the same margin of error that a sample size of n would produce:
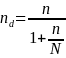
For
administrative reasons and to minimize the testing burden on
carriers, we set the maximum sample size per state and speed service
tier combination to 50 subscriber locations. When calculating the
margin of error associated with a 90% confidence level,
 = 1.645. A sample size of 50 (n
= 50) thus produces an
estimate with a margin of error plus and minus 11.5%. This means
that the test results from 50 locations will provide an estimation of
a carrier’s performance, relative to the performance standards,
that is 90 percent of the time accurate to plus or minus 11.5
percentage points.
= 1.645. A sample size of 50 (n
= 50) thus produces an
estimate with a margin of error plus and minus 11.5%. This means
that the test results from 50 locations will provide an estimation of
a carrier’s performance, relative to the performance standards,
that is 90 percent of the time accurate to plus or minus 11.5
percentage points.
Based on the equations defined above, the required sample size to achieve the target estimation precision is non-linearly proportionate to population size. In other words, as the total number of subscribers decreases, the sample size required to produce a comparable picture of a carrier’s network performance does not likewise decrease proportionally.
More specifically, as shown in the Figure below, the required sample size to achieve our target estimation precision of a 90% confidence level with a margin of error plus and minus 11.5% starts to decrease when the total number of subscribers is 2,500 or fewer. When the total number of subscribers decreases below 500 subscribers, the proportion of subscribers being tested (i.e., sample size divided by the total number of subscribers) increases sharply. This shows that the sample size required for a comparable picture of network performance is relatively more burdensome for carriers with fewer subscribers.
Figure. The respondent burden (orange) increases while total number of subscribers decreases.

To reduce the potential burden for those carriers, which tend to be smaller providers, we have set the sample size for a carrier with 500 or fewer subscribers, but greater than 50 subscribers, in a state and speed service tier to 10% of the total number of subscribers in that state and speed service tier. By requiring a fixed percentage of subscribers to be tested in these situations, we limit the burden on these carriers. For those with 50 subscribers or fewer in a single state and speed service tier, we set a sample size of 5 subscribers. We recognize that the resulting estimation precision is less than our target, but we find this necessary to account for the differences in resources and scale between larger and smaller carriers.
The table below highlights how, starting at 500 and fewer total subscribers, our “adjusted” sample sizes (i.e., the numbers of subscribers we are requiring carriers to test) differ from the nd “design” sample sizes necessary to achieve our target estimation precision of a 90% confidence level with an 11.5% MOE. The table also shows how the relative burdens differ for these two sets of sample size numbers, as well as the MOE associated with the adjusted sample sizes. For carriers with 500 or fewer subscribers in a state and speed service tier, the adjusted sample sizes reduce the burdens associated with testing up to 80%. Any further reduction of the sample sizes for these carriers would result in practically meaningless estimates because of the very low estimation precision.
design CL |
design MOE |
population size |
design sample size |
design respondent burden |
adjusted sample size |
adjusted respondent burden |
percent burden reduction |
MOE after adjustment |
90 |
11.5 |
50 |
25 |
0.500 |
5 |
0.100 |
80% |
34.9 |
90 |
11.5 |
75 |
30 |
0.400 |
8 |
0.100 |
75% |
27.5 |
90 |
11.5 |
100 |
34 |
0.340 |
10 |
0.100 |
71% |
24.7 |
90 |
11.5 |
120 |
36 |
0.300 |
12 |
0.100 |
67% |
22.5 |
90 |
11.5 |
150 |
38 |
0.253 |
15 |
0.100 |
61% |
20.1 |
90 |
11.5 |
200 |
40 |
0.200 |
20 |
0.100 |
50% |
17.4 |
90 |
11.5 |
250 |
42 |
0.168 |
25 |
0.100 |
40% |
15.6 |
90 |
11.5 |
300 |
43 |
0.143 |
30 |
0.100 |
30% |
14.2 |
90 |
11.5 |
350 |
44 |
0.126 |
35 |
0.100 |
20% |
13.2 |
90 |
11.5 |
400 |
45 |
0.113 |
40 |
0.100 |
11% |
12.3 |
90 |
11.5 |
450 |
45 |
0.100 |
45 |
0.100 |
0% |
11.6 |
90 |
11.5 |
500 |
46 |
0.092 |
50 |
0.100 |
|
11.0 |
90 |
11.5 |
1000 |
48 |
0.048 |
50 |
0.050 |
|
11.3 |
90 |
11.5 |
2500 |
50 |
0.020 |
50 |
0.020 |
|
11.5 |
90 |
11.5 |
5000 |
50 |
0.010 |
50 |
0.010 |
|
11.5 |
90 |
11.5 |
10000 |
50 |
0.005 |
50 |
0.005 |
|
11.5 |
90 |
11.5 |
20000 |
50 |
0.003 |
50 |
0.003 |
|
11.5 |
The individuals within the agency who consulted on the statistical aspects of the design are:
Cha-Chi Fan, Mathematical Statistician, 202-418-1554
Alec MacDonell, Telecommunications Systems Specialist, 202-418-0806
Cathy Zima, Supervisory Telecommunications Systems Specialist, 202-418-7380
The test result data will be collected by the Universal Service Administrative Company and analyzed by the individuals above, as well as other staff in the Industry Analysis Division of the Office of Economic Analytics. We do not anticipate seeking other additional assistance from outside the agency unit.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Cha-Chi Fan |
| File Modified | 0000-00-00 |
| File Created | 2024-09-24 |
© 2026 OMB.report | Privacy Policy