Summary Variance and Relative Standard Errors
Summary_Variances_and_Relative_Standard_Errors_(RSE).docx
Survey of Occupational Injuries and Illnesses
Summary Variance and Relative Standard Errors
OMB: 1220-0045
08/24/2023
S-31322 SAS - Calculate Summary Variances and Relative Standard Errors (RSE)
As a NO User,
I need the system to have the control/function to execute actions to calculate Summary Variances (SV) and Summary Relative Standard Errors (RSE) using the stored data and algorithm, so that the publishablility and reliability of the estimates can be determined.
Starting Point
This process will generate sampling errors and variances for all levels of estimates after State and national summary estimates have been calculated.
Definitions and assumptions
The SOII uses a Taylor series linearization methodology to calculate estimates of standard errors for published estimates.
Variance Estimation:
Calculate the variance for totals of case counts for each case type (TRC, DART, DAFW, DJTR, INJU, ORC, ILLN, SKIN, RESP, POIS, HEAR, OTHR), hours, and employment using the following unbiased formula for weighted samples
Where the number of usable units in the estimation stratum and the number of units in the sampling frame (which is the sum of final weights for this estimation stratum) equal 1, set the variance equal to 0
Where the number of usable units in the estimation stratum is greater than 1, the variance is calculated by the following:



where
 is
the total weighted estimate of the variable (case counts for each
case type, hours, employment) for all usable units in the estimation
stratum:
is
the total weighted estimate of the variable (case counts for each
case type, hours, employment) for all usable units in the estimation
stratum:

N is the sum of final weights for usable units in the estimation stratum:
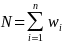
n is the number of usable units reporting in the estimation stratum
owi is the original state sampling weight of establishment i in the estimation
wi is the final weight of establishment I in the estimation stratum
xi is the reported value of the variable (case counts for each case type, hours, employment) for establishment i in the estimation stratum
 is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the
estimation
stratum:
is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the
estimation
stratum:
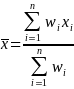
Where the number of usable units in the estimation stratum equals 1 and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, the mean of the stratum,
 cannot be used because it will yield an incorrect variance of 0.
To correct for this, use the mean from the roll-up hierarchy. That
is,
cannot be used because it will yield an incorrect variance of 0.
To correct for this, use the mean from the roll-up hierarchy. That
is,
If there is only one usable unit in the estimation stratum and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, calculate the variance as the variance of the roll-up level where the mean is the mean of the survey year, state, ownership, size class, and parent TEI of the usable units in this roll-up level. However, if the one usable unit in the estimation stratum is also the only usable unit for the survey year, state, ownership, size class, and parent TEI, continue to roll-up by parent TEI level as far as the industry domain level until the number of usable units is greater than 1.
If the one usable unit in the estimation stratum is also the only usable unit for the survey year, state, ownership, size class, and industry domain, calculate the variance as the variance of the roll-up level where the mean is the mean of survey year, state, ownership, size class 0 (all sizes) and TEI. Continue to roll-up the parent TEI level as far as TEI000000 (all industries) until the number of usable units is greater than 1.
Therefore, where the number of usable units in the estimation stratum equals 1 and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, we assign the roll-up level variance for this single usable unit; in other words, we use the roll-up level variance to approximate the variance for this single unit estimation stratum. The variance is calculated in the same way as those strata with more than one usable unit; it just includes all usable units at the roll-up level. Specifically the variance for the stratum with single usable unit is calculated as the following:



where
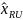 is
the total weighted estimate of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:
is
the total weighted estimate of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:

N is the sum of final weights for usable units in the estimation stratum:
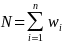 ,
in this case it is the single usable unit estimation stratum, so N=
,
in this case it is the single usable unit estimation stratum, so N=

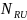 is
the sum of final weights for usable units in the roll-up level:
is
the sum of final weights for usable units in the roll-up level:

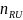 is
the number of usable units reporting in the roll-up level
is
the number of usable units reporting in the roll-up levelowi is the original state sampling weight of establishment i in the roll-up level
wi is the final weight of establishment i in the roll-up level
xi is the reported value of the variable (case counts for each case type, hours, employment) for establishment i in the roll-up level
 is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:
is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:

Covariance Estimation:
Calculate the covariance for total case counts for each case type with hours
Where the number of usable units in the estimation stratum and the number of units in the sampling frame (which is the sum of final weight in this estimation stratum) equal 1, set the covariance equal to 0.
Where the number of usable units in the estimation stratum is greater than 1, the covariance is calculated by the following:


where
 is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:
is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:

 is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:
is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:

N is the sum of final weights for usable units in the estimation stratum:
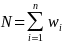
n is the number of usable units reporting in the estimation stratum
owi is the original state sampling weight of establishment i in the estimation stratum
wi is the final weight of establishment i in the estimation stratum
xi is the reported value of the variable (case counts for each case type) for establishment i in the estimation stratum
 is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the estimation
stratum:
is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the estimation
stratum:
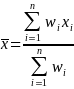
yi is the reported value of the variable (hours) for establishment i in the estimation stratum
 is
the weighted average value of the variable (hours) for all usable
units in the estimation stratum:
is
the weighted average value of the variable (hours) for all usable
units in the estimation stratum:
Where the number of usable units in the estimation stratum equals 1 and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, the means of the stratum,
 and
and
 cannot be used because it will yield an incorrect covariance of 0.
To correct for this, use the means from the roll-up hierarchy:
cannot be used because it will yield an incorrect covariance of 0.
To correct for this, use the means from the roll-up hierarchy:
If there is only one usable unit in the estimation stratum and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, calculate the variance as the variance of the roll-up level where the mean is the mean of the survey year, state, ownership, size class, and parent TEI of the usable units in this roll-up level. However, if the one usable unit in the estimation stratum is also the only usable unit for the survey year, state, ownership, size class, and parent TEI, continue to roll-up by parent TEI level as far as the industry domain level until the number of usable units is greater than 1.
If the one usable unit in the estimation stratum is also the only usable unit for the survey year, state, ownership, size class, and industry domain, calculate the variance as the variance of the roll-up level where the mean is the mean of survey year, state, ownership, size class 0 (all sizes) and TEI. Continue to roll-up the parent TEI level as far as TEI000000 (all industries) until the number of usable units is greater than 1.
Therefore, where the number of usable units in the estimation stratum equals 1 and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, similarly we use the roll-up level covariance as the covariance for the singe usable unit estimation stratum. The approximate covariance for the stratum with single usable unit is calculated by the following:
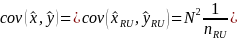

where
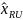 is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the roll-up level:
is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the roll-up level:

 is
the total weighted estimate of the variable (hours) for all usable
units in the roll-up level:
is
the total weighted estimate of the variable (hours) for all usable
units in the roll-up level:

N is the sum of final weights for usable units in the estimation stratum:
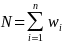 ,
in this case it is the single usable unit estimation stratum, so N=
,
in this case it is the single usable unit estimation stratum, so N=

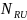 is
the sum of final weights for usable units in the roll-up level:
is
the sum of final weights for usable units in the roll-up level:

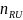 is
the number of usable units reporting in the roll-up level
is
the number of usable units reporting in the roll-up levelowi is the original state sampling weight of establishment i in the roll-up level
wi is the final weight of establishment i in the roll-up level
xi is the reported value of the variable (case counts for each case type) for establishment i in the roll-up level
 is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:
is
the weighted average value of the variable (case counts for each
case type, hours, employment) for all usable units in the roll-up
level:

yi is the reported value of the variable (hours) for establishment i in the roll-up level
 is
the weighted average value of the variable (hours) for all usable
units in the roll-up level:
is
the weighted average value of the variable (hours) for all usable
units in the roll-up level:
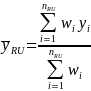
Variance of Ratios:
Where the number of usable units in the estimation stratum and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) equal 1, set the variance equal to 0.
Where the number of usable units in the estimation stratum is greater than 1, calculate the variance of the ratio of total case counts for each case type (x) and hours (y) (
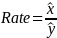 )
using the following unbiased formula for weighted samples
)
using the following unbiased formula for weighted samples

where
 is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:
is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:

 is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:
is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:

 is
the variance estimate of the variable in
the estimation stratum
(total case counts for each case type (
is
the variance estimate of the variable in
the estimation stratum
(total case counts for each case type ( ))
)) is
the variance estimate of the variable in
the estimation stratum
(total hours (
is
the variance estimate of the variable in
the estimation stratum
(total hours ( ))
)) is
the covariance estimate between two variables in
the estimation stratum
(case counts of each case type and hours)
is
the covariance estimate between two variables in
the estimation stratum
(case counts of each case type and hours)
If a standard rate per 100 employees (equivalent 200,000 employee
hours per year) is reported ( ),
then the variance of standard rate for case types TRC, DART,
DAFW, DJTR, ORC, and INJU is
),
then the variance of standard rate for case types TRC, DART,
DAFW, DJTR, ORC, and INJU is

Where
the standard rate per 10,000 employees (equivalent 20,000,000
employee hours per year) is reported ( ),
then the variance
of standard rate
for case types ILLN, SKIN, RESP, POIS, HEAR, OTHR is
),
then the variance
of standard rate
for case types ILLN, SKIN, RESP, POIS, HEAR, OTHR is

Where the number of usable units in the estimation stratum equals 1 and the number of units in the sampling frame (which is the sum of final weights in this estimation stratum) does not equal 1, calculate the variance of the ratio as the variance of total case counts for each case type (x) and hours (y) of the roll-up level used above, using the following unbiased formula for weighted samples

where
 is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:
is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the estimation stratum:

 is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:
is
the total weighted estimate of the variable (hours) for all usable
units in the estimation stratum:

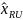 is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the roll-up level:
is
the total weighted estimate of the variable (case counts for each
case type) for all usable units in the roll-up level:

 is
the total weighted estimate of the variable (hours) for all usable
units in the roll-up level:
is
the total weighted estimate of the variable (hours) for all usable
units in the roll-up level:

 is
the variance estimate of the variable (total case counts for each
case type (
is
the variance estimate of the variable (total case counts for each
case type ( ))
for the roll-up level
))
for the roll-up level is
the variance estimate of the variable (total hours (
is
the variance estimate of the variable (total hours ( ))
for the roll-up level
))
for the roll-up level is
the covariance estimate between two variables (case counts of each
case type and hours) for the roll-up level
is
the covariance estimate between two variables (case counts of each
case type and hours) for the roll-up level
If
a standard rate per 100 employees (equivalent 200,000 employee hours
per year) is reported ( ),
then the variance
of standard rate
for the roll-up level for case types TRC, DART, DAFW, DJTR, ORC, and
INJU is
),
then the variance
of standard rate
for the roll-up level for case types TRC, DART, DAFW, DJTR, ORC, and
INJU is

Where
the standard rate per 10,000 employees (equivalent 20,000,000
employee hours per year) is reported ( ),
then the variance
of standard rate
for the roll-up level for case types ILLN, SKIN, RESP, POIS, HEAR,
OTHR is
),
then the variance
of standard rate
for the roll-up level for case types ILLN, SKIN, RESP, POIS, HEAR,
OTHR is
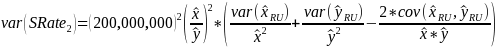
Percent Relative Standard Error (RSE) Estimation:
Calculate the percent relative standard error using the following formulas
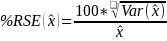 for totals
for totals
where
 is
the total estimate of the variable (case counts for each case type,
hours, and employment) for all usable units in the stratum. Note
that the estimate may be derived from a single usable unit or
multiple usable units.
is
the total estimate of the variable (case counts for each case type,
hours, and employment) for all usable units in the stratum. Note
that the estimate may be derived from a single usable unit or
multiple usable units. is
the variance estimate of the variable (case counts for each case
type, hours, and employment). Note where the number of usable units
in the estimation stratum equals 1 and the number of units in the
sampling stratum is greater than 1, the roll-up level variance was
used to approximate the variance for the single unit stratum.
is
the variance estimate of the variable (case counts for each case
type, hours, and employment). Note where the number of usable units
in the estimation stratum equals 1 and the number of units in the
sampling stratum is greater than 1, the roll-up level variance was
used to approximate the variance for the single unit stratum.
 for rates
for rates
where
 is
the total estimate of the variable (total case counts for each case
type) for all usable units in the estimation stratum
is
the total estimate of the variable (total case counts for each case
type) for all usable units in the estimation stratum is
the total estimate of the variable (total hours) for all usable
units in the estimation stratum
is
the total estimate of the variable (total hours) for all usable
units in the estimation stratum
 is
the variance estimate of the standard rate. Note
where the number of usable units in the estimation stratum equals 1
and the number of units in the sampling stratum is greater than 1,
the roll-up level variance of the ratio was used to approximate the
variance of the ratio for the single unit stratum.
is
the variance estimate of the standard rate. Note
where the number of usable units in the estimation stratum equals 1
and the number of units in the sampling stratum is greater than 1,
the roll-up level variance of the ratio was used to approximate the
variance of the ratio for the single unit stratum.
 is
the standard rate of case counts to hours depending on which case
type is being used.
is
the standard rate of case counts to hours depending on which case
type is being used.
Estimation for domain levels
Estimation domains for both national and state estimates are combinations of year, state, ownership, TEI, and reported size class.
For variance estimates, calculate the estimate at the finest detail: survey year, state, ownership, TEI, and reported size class. The variances of counts of broader levels are calculated as the sum of the finer levels that comprise the broad level. For example, the variance of counts of the survey year, state, ownership, TEI (i.e., reported size class 0) is the sum of the variances of the survey year, state, ownership, TEI of reported size classes 1-5.
The variances of rates of broader levels cannot be calculated as the sum of variances of the finer levels that comprise the broad level. Instead, they are calculated using all the usable units in the estimation domain. For example, the variance of the rate of the survey year, state, ownership, TEI (i.e., reported size class 0) is calculated using all the usable units from size class 1-5.
If
 is
equal to 0, then the variance, and covariance and RSE for
is
equal to 0, then the variance, and covariance and RSE for
 and
and
 are
equal to 0.
are
equal to 0.
Estimates are based on the reported size class of the establishment. The number of usable units in an estimation stratum is based on the reported size class, not the size class used for sampling.
Data for the mining (NAICS 212) and railroad industries (NAICS 482) are obtained from MSHA an FRA, respectively, and are considered a census. Since these data are obtained from outside sources for which there is no ability to assess reliability, set the variance and covariance estimates for these industries to NULL/missing values before summarization for any estimation domain of interest. This means MHSA and FRA strata only contribute to point estimates (total and rate).
Inputs
Microdata
Summary case counts
Final state and national summary weights (output from 8.1.5)
List of Target Estimation Industries (TEIs)
Processing steps
Calculate Variances and RSEs based on the formulas described in the definition for 14 for W weighted count estimates (results for the W Estimates for the twelve case types, hours, and employment are copied to the 14 T estimates) and 12 for R Estimates (for the twelve case types)
Outputs
Variance (14 for W weighted count estimates (results for the W Estimates for the twelve case types, hours, and employment are copied to the 14 T estimates) and 12 for R Estimates (for the twelve case types))
Percent Relative Standard Errors (14 for W weighted count estimates (results for the W Estimates for the twelve case types, hours, and employment are copied to the 14 T estimates) and 12 for R Estimates (for the twelve case types))
S-31323 SAS - Summary Variances (SV) and SV Relative Standard Errors (RSE) errors
As a NO User,
I need the system to have the ability to feed any errors and details relating to Summary Variances (SV) and SV Relative Standard Errors (RSE) calculation to the Error Monitoring GUI
So that errors in Estimation Runs can be view
Error checking for Variance and RSE:
Check that rate (R), weighted count (W), and weighted count in thousands (T), have RSEs. Census industries (railroad and mining) we don’t calculate RSEs for. Also, we don’t calculate RSE for quartile estimates.
select count(*), estimate_type from soii.estimates where rse is not null and survey_year=XXXX group by estimate_type
expect W, R, and T rows to have >0 for count
System should not calculate size class estimates for state estimates unless it is a sector level TEI (current system: LEVEL_CODE<3).
Very small variances should be set to zero. Set variances less than the absolute value of 0.000005 to zero.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Bajaj, Bhavdeep - BLS CTR |
| File Modified | 0000-00-00 |
| File Created | 2024-07-24 |
© 2025 OMB.report | Privacy Policy