Part B_TechHire_3rd_package
Part B_TechHire_3rd_package.docx
TechHire and Strengthening Working Families Initiative Grant Programs Evaluation18-Month Follow-Up Survey
OMB: 1290-0027
Evaluation of Strategies Used in the TechHire and Strengthening Working Families Initiative Grant Programs
ICR REF 201905-1290-001
MAY 2019
PART B. COLLECTIONS OF INFORMATION EMPLOYING STATISTICAL METHODS
In this document, we discuss the statistical methods to be used in the data collection activities for the Evaluation of Strategies Used in the TechHire and Strengthening Working Families Initiative (SWFI) Grant Programs. This study is sponsored by the Chief Evaluation Office (CEO) and Employment and Training Administration (ETA) in the U.S. Department of Labor. The purpose of the evaluation is to identify whether the grants help low-wage workers obtain employment in and advance in H-1B industries and occupations and, if so, which strategies are most helpful. CEO has contracted with Westat and its subcontractor, MDRC, to conduct this evaluation. The evaluation includes three components: an implementation study, a randomized controlled trial (RCT) study, and a quasi-experimental design (QED) study.
This request for clearance includes the 18-month follow-up survey.
B.1 Respondent Universe and Sampling Methods
B.1.1 Respondent Universe
The respondent universe consists of all individuals who are randomized to participate in the TechHire or SWFI treatment or the control group during the study intake period (between April 2018 and October 2019). We do not plan to select a sample. Table B.1.1 shows the expected enrollment in each RCT site.We expect that a total of 1,704 individuals will be randomly assigned (852 in the treatment group and 852 in the control group).
Table B.1.1 Expected RCT Assignment
Grantee |
Program |
Treatment |
Control |
Total |
Vermont Technical College |
SWFI |
100 |
100 |
200 |
Community College of Aurora |
SWFI |
220 |
220 |
440 |
Career Source Tampa Bay |
TH |
300 |
300 |
600 |
LaGuardia Community College |
TH |
112 |
112 |
224 |
Daytona State College |
TH |
120 |
120 |
240 |
Total |
|
852 |
852 |
1,704 |
B.2 Procedures for the Collection of Information
B.2.1 Statistical Methodology for Stratification and Sample Selection
No sampling methods will be used as all individuals will be included in the follow-up data collection effort.
B.2.2 Estimation Procedures
The objective of the RCT is to estimate program impacts—that is, observed outcomes for the treatment group relative to what those outcomes would have been in the absence of the program—in each of the six RCT study sites. Specifically, the RCT will identify the extent to which training and supportive services in each site improve participant employment and earnings.
This section describes our analytic approach to estimate program impacts using the 18-month survey that is included in this request for clearance, as well as the National Directory of New Hires (NDNH) data. The 18-month survey is intended to capture impacts on intermediate outcomes of educational and training completion, removal of work-related barriers, including transportation and childcare, and employment, earnings, and job characteristics, and material well-being. Key outcome variables include training completion, industry of training, credential attainment, has regular child care arrangement, receives child care subsidy, ever worked, currently working, current/most recent job industry, hours worked, and hourly wage, public assistance receipt, and household and personal income.
Given that random assignment produces balance in expectation, the basic impact estimates can be computed using the difference in mean outcomes between the treatment group members and control group members. Each of the resulting estimates for each outcome is unbiased because the individuals who comprise the treatment and control groups in the site were assigned at random to either the treatment or control from a common pool and hence are expected to be statistically equivalent on all factors at baseline. As a result, any statistically significant differences in outcomes between the groups can be attributed to the effects of the intervention. Regression analysis that controls for background characteristics, including prior earnings and employment, education, and demographics, will be used to improve the precision of the impact estimates. A standard linear regression will be used to estimate impacts. This approach is used in all impact analyses that we are aware of over the past 40 years. The rationale for this standard approach, of using inferential (rather than descriptive) statistics, rests on the goal to generalize the results to a super population of TechHire and SWFI grantees. Even though probability sampling was not used to select the sites, an effort was made to ensure that the grantees chosen for the impact analysis cover a range of program features, geographic regions, and populations. DOL hopes to learn not only about these specific five grantees, but to generalize these findings to the dozens of TechHire grantees throughout the nation.1
We plan to pool the data across sites for the impact estimates and to cluster some of the sites—for example, to group by TechHire and SWFI grantees. Pooling sites is necessary due to the small sizes of some of the sites and because the policy question is whether the training and supportive services provided under the grants helped low-wage jobseekers find and maintain employment. The pooled estimate provides a bottom-line indicator across a range of sites. We will add site indicator dummies to the linear regression models in order to account for site fixed effects.
Impacts will be calculated for key subgroups to better understand what works best for whom. In impact studies, subgroup impacts have been estimated several different ways. In “split-sample” subgroup analyses, the full sample is divided into two or more mutually exclusive and exhaustive groups (for example, by gender or for those with more severe barriers and less work experience). In this approach, impacts are estimated for each group separately. In addition to determining whether the intervention had statistically significant effects for each subgroup, Q-statistics are used to determine whether impacts differ significantly across subgroups (Hedges & Olkin, 1985). Regardless of the exact subgroup estimation strategy, it is clear that subgroups would have to be computed on the pooled sample rather than with sites.
We will strive to limit subgroup comparisons to those for which theory and prior studies provide good reasons for expecting subgroup differences on advancement outcomes. This is to guard against the chance of a “false positive,” which stems from the fact that the more subgroups that are examined, the greater the chance of finding one with a large effect, even when there are no real differences in impacts across subgroups. We will also consider the use of corrections for multiple comparisons, such as the Bonferroni or Benjamini-Hochberg corrections.
B.2.3 Degree of Accuracy Needed
Based on the selection of 5 grantees for the RCT study, we believe that the sites will be able to take in a total of 1,704 participants. B.2.3 shows the Minimum Detectable Effects (MDEs) for a few different scenarios:2
A scenario in which we pool 5 sites with a total sample size of 1,700
A scenario in which we pool 3 TechHire sites
A scenario in which we pool 2 SWFI sites
Within each of these three sample sizes, MDEs are shown based on the expected sample sizes for both the administrative records data (which are assumed to cover all sample members) and the survey data (which are assumed to cover 80 percent of sample members).3 The four rightmost columns of the table show the MDEs for impacts on percentage measures, such as employment, assuming two different standard deviations (0.4 and 0.5)4 and continuous measures, such as earnings, assuming two different standard deviations ($8,500 and $14,000).5 The third column of the table presents the Minimum Detectable Effect Size (MDES).
Table B.2.1 shows MDEs for the scenario in which all 5 sites are pooled. Assuming 50 percent of the control group was employed (that is, the standard deviation is 0.5), the MDESs of 0.111 and 0.1124 translate into MDEs of between 5.6 and 6.2 for percentage measures. MDES for earnings measures are also shown. Depending on the control group levels, annual earnings impacts would have to be in the $900-$1,600 range to have a reasonable chance of being statistically significant. Based on past studies it would be reasonable to expect impacts of this size.
Table B.2.1 also shows MDEs for the scenarios in which the sites are clustered by program—TechHire and SWFI. As discussed above, a common threshold for a well powered estimate is that MDESs should be able to detect impacts which are smaller than 0.21 standard deviations different from the control group level. MDES for grantee’s at this level are acceptable. Under the scenario of 2 pooled SWFI sites MDES are .181 and translate into employment effects in the 9 or 10 point range and earnings effects between $1400-$2500.
Table B.2.1. Minimum Detectable Effects for Key Outcomes
|
MDE |
||||||||
Employment |
|
Annual earnings |
|||||||
Sample |
Sample Size |
MDESa |
|
SD = 0.4 |
SD = 0.5 |
|
SD = 8,000 |
SD = 14,000 |
|
Assuming 5 sites |
|
|
|
|
|
|
|
|
|
|
Total pooled sample |
|
|
|
|
|
|
|
|
|
Administrative records |
1,704 |
0.111 |
|
4.4 |
5.6 |
|
888 |
1,554 |
|
Survey |
1,363 |
0.124 |
|
5.0 |
6.2 |
|
992 |
1,736 |
|
|
|
|
|
|
|
|
|
|
|
TechHire pooled sample (3 sites) |
|
|
|
|
|
|
|
|
|
Administrative records |
1,064 |
0.141 |
|
5.6 |
7.1 |
|
1,128 |
1,974 |
|
Survey |
851 |
0.157 |
|
6.3 |
7.9 |
|
1,256 |
2,198 |
|
|
|
|
|
|
|
|
|
|
|
SWFI pooled sample (2 sites) |
|
|
|
|
|
|
|
|
|
Administrative records |
640 |
0.181 |
|
7.2 |
9.1 |
|
1,448 |
2,534 |
|
Survey |
512 |
0.203 |
|
8.1 |
10.2 |
|
1,624 |
2,842 |
|
|
|
|
|
|
|
|
|
|
SOURCE: MDRC calculations using PowerUP! tool.
NOTES: MDES = minimum detectable effect size; MDE = minimum detectable effect; SD = standard deviation.
aMDES are for a two-tailed test at 0.10 significance with 80 percent power. These MDES assume covariates will be used, and that they will have a moderate effect (R-squared=0.15).
B.2.4 Unusual Problems Requiring Specialized Sampling Procedures
None.
B.2.5 Any use of periodic (less frequent than annual) data collection cycles to reduce burden.
There is no use of less than annual data collection cycles because of the relatively short duration of the grant programs being evaluated. This survey is for a one time survey to be conducted 18 months after random assignment.
B.3 Methods to Maximize Response Rates and to Deal With Issues of Nonresponse
B.3.1 Methods to Maximize Response Rates
Participants will be offered a $50 incentice to complete the survey in the first four weeks on the web, and a $40 incentive to complete it after the first four weeks by web or telephone. The advance letters will also include a $5 prepaid incentive. Providing participants with a monetary incentive reduces non-response bias and improves representativeness, especially in low-income populations.[1],[2],[3], [5] A high response rate is especially important for ensuring unbiased impact estimates. Incentives are an essential component of the multi-pronged approaches used to minimize non-response bias, especially in studies with hard-to-reach, low-income individuals; [6] reduce efforts to locate hard-to-reach study participants; and lower overall survey costs and time to achieve completion rates without affecting data quality[7],[8].
The sequential multi-mode data collection approach includes the administration of a web survey to study participants (treatment and control groups) in the five RCT sites followed by telephone calls to nonrespondents to complete a computer-assisted telephone interview (CATI). Our goal for the 18-month follow-up survey is an 80 percent response rate. Westat has achieved 80 percent or higher response rates for similar studies. For example, the Mental Health Treatment Study (MHTS), which Westat conducted for Social Security Administration (SSA), included seven quarterly follow-up surveys with RCT study participants in the treatment and control groups after random assignment. Westat achieved over 80 percent response rates in all seven quarters, including over 80 percent response rates for both the treatment and control groups for each quarterly survey prior to quarter 6.
Figure B.3.1 provides a flowchart of the data collection methodology to be used for the 18-month follow-up survey. Cohorts will be released for survey fielding each month. Participants will be mailed an invitation letter via first class postal mail with study information that contains the web survey URL and a unique PIN to access the survey. A set of frequently asked questions (FAQs) will also be included on the back of the invitation letter along with a sponsorship letter from DOL to help add credibility to the study, and to encourage participation. The invitation will also provide a phone number and email address for participants to contact Westat for technical assistance. We will also send an invitation email to those cases where we have their email address from the baseline intake phase. Our experience shows that response rates are slightly higher on web surveys when sampled members can click on a personalized web survey link within an email compared to entering a URL from a postal letter. In order to decrease respondent burden and to improve response rates, the web survey will be accessible across a wide array of computer configurations and mobile devices. Based on the baseline data collection thus far, we anticipate that the vast majority of participants will have email addresses.
One week following the initial invitation mailing, participants will receive the first of three weekly reminders. Participants with email addresses will receive an email reminder, and those without an email address will receive the reminder letter via postal mail encouraging their participation in the survey. The second and final weekly reminder will be sent out to nonrespondents similarly to the first weekly reminder. The final reminder will encourage sample members to complete the web survey and inform them that we will contact those who have not completed the web survey by telephone. Additionally, SMS text messages will also be sent at the same time as the weekly email reminders to those participants who provide permission to text them. Cell phone number and permission to text were asked in the baseline information form (BIF) and 6-month follow-up survey.
Figure B-1. Proposed data collection flow for the 18-month follow-up Survey
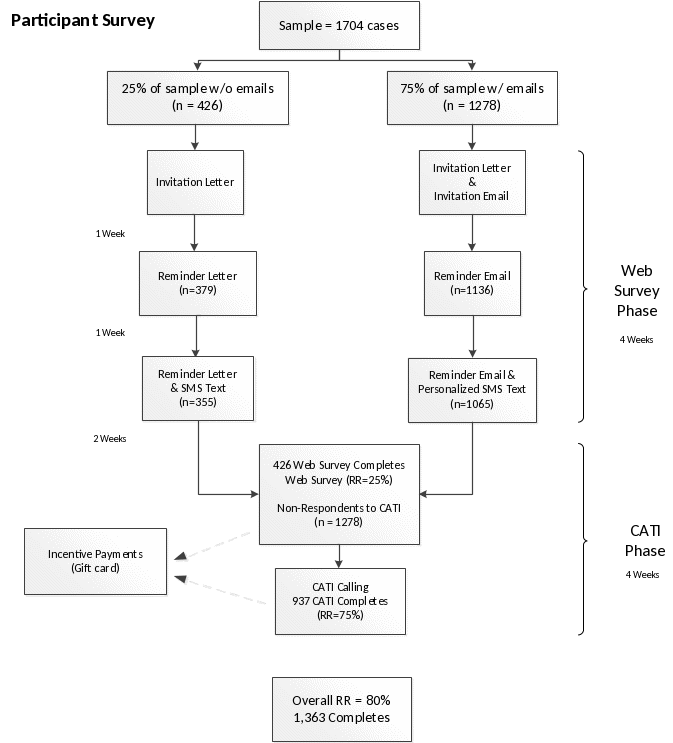
B.3.2 Nonresponse Bias Analysis
Even though intensive methods will be used to increase response rates non-response bias is still a concern. Survey nonresponse can bias the impact estimates if the outcomes of survey respondents and nonrespondents differ, or if the types of individuals who respond to the survey differ across the treatment and control groups. We will use several methods to assess the effects of survey nonresponse using data collected for the study.
During data collection, we will take steps to understand, monitor, manage and address potential sources of non-response bias. During the survey fielding period, we will review contact attempts and disposition status which will enable us to monitor response rates by cohort (defined by time of random assignment), research group, and site. Should significant gaps in response rates among these groups occur, we will intensify recruitment efforts for the affected group. This will include prioritizing the efforts of the most experienced survey interviewers towards the affected group.
We will examine nonresponse using data collected for the study. First, we will use baseline data (which will be available for the full research sample) to conduct statistical tests (chi-squared and t-tests) to gauge whether treatments who respond to the interviews are fully representative of all treatment group members, and similarly for control group members. Noticeable differences in the characteristics of survey respondents and nonrespondents could suggest the presence of nonresponse bias. Furthermore, we will test whether the baseline characteristics of respondents in the two research groups differ from each other. Although baseline characteristics for the full sample should not differ much between the program and control groups, significant differences between program and control group respondents could mean that impacts estimated from surveys will confound program impacts with pre-existing differences between the groups.
Second, we will assess nonresponse bias using administrative records data. For example, we will examine whether impacts on employment rates differ by respondent status. If program impacts are substantially different for respondents and nonrespondents, that would make us more cautious about drawing conclusions from the survey.
We will use several approaches to correct for potential nonresponse bias in the estimation of program impacts. First, we will adjust for observed differences between treatment and control group respondents using regression models. Second, because this regression procedure will not correct for differences between respondents and nonrespondents in each research group, we will construct sample weights so that the weighted observable baseline characteristics of respondents are similar to the baseline characteristics of the full sample of respondents and nonrespondents. We will construct weights for treatment and control group members using the following three steps:
Estimate a logit model predicting survey response. The binary variable indicating whether or not a sample member is a respondent will be regressed on baseline measures.
Calculate a propensity score for each individual in the full sample. This score is the predicted probability that a sample member is a respondent, and will be constructed using the parameter estimates from the logit regression model and the person’s baseline characteristics. Individuals with large propensity scores are likely to be respondents, whereas those with small propensity scores are likely to be nonrespondents.
Construct nonresponse weights using the propensity scores. Individuals will be ranked by the size of their propensity scores, and divided into several groups of equal size. The weight for a sample member will be inversely proportional to the mean propensity score of the group to which the person is assigned.
This propensity score procedure will yield large weights for those with characteristics that are associated with low response rates (that is, for those with small propensity scores). Similarly, the procedure will yield small weights for those with characteristics that are associated with high response rates. Thus, the weighted characteristics of respondents should be similar, on average, to the characteristics of the entire research sample.
It is important to note that the use of weights and regression models adjusts only for observable differences between survey respondents and nonrespondents in the two research groups. The procedure does not adjust for potential unobservable differences between the groups. Thus, our procedures will only partially adjust for potential nonresponse bias. We will use administrative data to assess whether such bias is present in our data, as discussed above.
Records with missing values on dependent (or outcome) variables will be excluded from the impact estimates for those variables. This includes records for participants who do not respond to the entire survey, as well as records for participants who do not answer individual questions. As a sensitivity check, we will use multiple imputation of survey outcomes as suggested by Puma et al, 2009.
B.4 Test of Procedures or Methods to be Undertaken
The 18-month follow-up survey was pretested before submission to OMB. For the pretest, 7 individuals were recruited from the TechHire program at Montgomery College in Rockville, MD and a One-Stop Center in New York City. Pretests were conducted over the phone. Individuals were paid $50 for their participation in the pretest. The pretest used retrospective probing in which respondents completed the full survey and were then probed about the clarity of the questions and any potential problems with the instrument. The benefit of retrospective probing is that it allowed us to estimate the burden. The version of the instrument submitted to OMB incorporates the pretest results and no changes are anticipated. In terms of burden, the average time to complete the survey was 30 minutes, although the time varied based on whether the respondent was employed, participated in job training, or were parents, as these determined major skip patterns.
B.5 Individuals Consulted on Statistical Methods and Individuals Responsible for Collecting and/or Analyzing the Data
B.5.1 Individuals Consulted on Statistical Methods
Westat
Dr. Joseph Gasper (240) 314-2470
Dr. Steve Bell (301) 294-2065
MDRC
Dr. Richard Hendra (212) 340-8623
Ms. Kelsey Schaberg (212) 340-7581
B.5.2 Individuals Responsible for Collecting/Analyzing the Data
Westat
Dr. Joseph Gasper (240) 314-2470
Mr. Wayne Hintze (301) 517-4022
MDRC
Dr. Richard Hendra (212) 340-8623
Ms. Kelsey Schaberg (212) 340-7581
1 Bloom et al, 2017 assert that these types of inferences to a super population are appropriate even in the case of convenience sampling: “Even in a convenience sample, sites are usually chosen not because they comprise a population of interest but rather because they represent a broader population of sites that might have participated in the study or might consider adopting the program being tested. Hence, the ultimate goal of such studies is usually to generalize findings beyond the sites observed, even though the target of generalization is not well-defined.”
2
The minimal detectable effects were estimated using the following
formula from Bloom et al. 2006:![]() .
.
Here the Y terms refer to the means for treatment and control group members (subscripted by T and C). M is the multiplier, which is a constant that factors in the statistical power (here 0.8), the statistical significance (here 0.1), and the number of degrees of freedom in the impact analysis equation. In the two tailed test scenario that we have used here, M = 2.49. The term on the right is the standard error which is computed by dividing the variance (σ2) by the random assignment ratio (P).
3 The MDESs presented are for a two-tailed test at 0.10 significance level with 80 percent power. These MDES assume 50 percent of the sample is assigned to the treatment group and 50 percent is assigned to the control group, that 10 covariates will be used, and that the covariates will have a weak relationship with the outcomes (R-squared=0.15). This R-squared value is somewhat low compared to what’s been observed in other training and employment studies, and is intentionally a fairly conservative estimate. If the covariates actually explain more of the variation in outcomes, this will only increase the power of the study.
4A standard deviation of 0.5 assumes the worst case scenario. The point of maximum variance for a percentage measure is 0.5 (a control group level of 50 percent). At that point, an MDES of 0.2 translates into an MDE of 10 percentage points. The further the variance is from 0.5, the smaller the MDE. For example, if the control group level for a measure is 20 percent, the MDE for a study powered at 80 percent would be 8 percentage points.
5These standard deviations are based on standard deviations from MDRC’s evaluation of the WorkAdvance program (Hendra et al., 2016).
[1][1] Singer E. (2002). The use of incentives to reduce non response in households surveys in: Groves R, Dillman D, Eltinge J, Little R (eds.) Survey Non Response. New York: Wiley, pp 163-177.
[2][2] James T. (1996). Results of wave 1 incentive experiment in the 1996 survey of income and program participation. Proceedings of the Survey Research Section, American Statistical Association., 834-839.
[3][3] Groves R, Fowler F, Couper M, Lepkowski J, Singer E. (2009) in: Survey methodology. John Wiley & Sons, pp 205-206.
[5][5] Singer E and Ye C. (2013). The use and effectives of incentives in surveys. Annals of the American Academy of Political and Social Science, 645(1):112-141.
[6][6] Bonevski B, Randell M, Paul C, Chapman K, Twyman L, Bryant J, Brozek K, Hughes, C. (2014) Reaching the hard-to-reach: a systematic review of strategies for improving health and medical research with socially disadvantaged groups. BMC Medical Research Methodology 14:42, 14-42. http://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-14-42
[7][7] Dillman, Don. 2000. Mail and Internet Surveys: The Tailored Design Method, 2nd Edition. John Wiley & Sons: New York.
[8][8] Singer, Eleanor. 2006. “Introduction: Nonresponse Bias in Household Surveys,” Public Opinion Quarterly. 70(5): 637-645.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 0000-00-00 |
© 2026 OMB.report | Privacy Policy