YCC_OMB Part B Justification_to DOL_CLEAN_03072018X
YCC_OMB Part B Justification_to DOL_CLEAN_03072018.DOCX
Youth CareerConnect Evaluation
OMB: 1290-0016
Evaluation of Youth CareerConnect (YCC)
OMB SUPPORTING STATEMENT PART B
The U.S. Department of Labor’s (DOL), Employment and Training Administration (ETA), in collaboration with the Chief Evaluation Office (CEO), is undertaking the Evaluation of Youth CareerConnect (YCC). The overall aims of the evaluation are to determine the extent to which the YCC program improves high school students’ education and employment outcomes and to assess whether program effectiveness varies by student and program characteristics. The evaluation is based on impact and implementation studies. The impact study has two components: (1) a rigorous randomized controlled trial (RCT) design component in which program applicants were randomly assigned to a treatment group (and were able to receive YCC program services) or a control group (who were not), and a quasi-experimental design (QED) component based on administrative school records. ETA has contracted with Mathematica Policy Research (Mathematica) and its subcontractor, Social Policy Research Associates (SPR), to conduct this evaluation.
With this package, clearance is requested for the follow-up survey data collection of study participants in the RCT districts
Prior clearance was received on April 15, 2015, under OMB Control No. 1291-0003 for four data collection instruments related to the impact and implementation studies to be conducted as part of the evaluation. The full package for the study is being submitted in two parts because the study schedule required the random assignment and the implementation study to begin before the follow-up instruments had been developed and tested.
1. Respondent universe and sampling
The RCT component includes four districts, three of which will have students participate in the follow-up surveying and one of which will use data from school records only.
After clarifying information provided by all 24 YCC grantees in their grant applications, Mathematica conducted one-day, in-person visits to 14 districts with potential for inclusion in the RCT (These activities were approved under OMB Approval No. 1205-0436). After the visits, the field was narrowed to 10 districts that met three criteria: (1) enough student demand to generate a control group, (2) feasibility of implementing random assignment procedures, and (3) a significant contrast between the services available to the treatment and control groups.
Random assignment was attempted in these districts. Although all districts initially seemed feasible, one could not provide the information needed to participate in the evaluation and five others did not have sufficient excess demand to generate treatment and control groups. Random assignment into the YCC program occurred in the remaining four districts. In these four districts, students who were assigned to the treatment group were invited to enroll in their YCC program, and those assigned to the control group were informed that they were not eligible to enroll in the program but could enroll in similar programs in their area.
Of the four remaining districts, baseline data and consent to be in the evaluation could be collected on treatment and control group students in only three. These three districts will participate in the follow-up data collection effort covered in this request, and the fourth will remain in the RCT using school records only. Because these districts were selected (and thus do not constitute a random sample of all 24 grantees that received YCC grant funds), the student universe does not consist of all eligible program applicants nationwide, and the study sample is not necessarily representative of all YCC students nationally.
The period for recruiting and enrolling students in the evaluation varied among these three districts. One district began recruiting in fall 2015, and the last district ended recruitment in summer 2017. On average, intake at each district took approximately three to four months. These districts recruited and screened potential YCC program participants using their regular procedures, but they included in the application packet the evaluation’s parent consent, student assent, and baseline information form (BIF) materials (OMB Control No. 1291-0003). Program staff were provided with background materials on the evaluation and were trained to answer questions from parents and students about the evaluation and their participation.
The sample for the study (including follow-up surveying) consists of approximately 540 study participants across the three districts, 345 of whom who were allowed to enroll in YCC program services and 195 of whom (the control group) were not able to enroll.
2. Procedures for collecting information
The impact study will rigorously assess the causal effect of YCC by answering the following general research question: What is the impact of the YCC on critical milestones that participants can achieve in high school and on momentum points associated with participants’ education and employment success?
Follow-up surveys will be attempted with 540 treatment and control group members at the three RCT districts that will be part of this data collection effort. Study participants will be notified about the survey request via mail, email, text message, and phone. A multimode approach that uses three phases of data collection will help achieve a response rate of at least 80 percent and maintain maximum efficiency. In the first phase, study participants will be directed to the web survey or to call in to Mathematica’s Survey Operations Center (SOC) to complete the survey using computer assisted telephone interviewing (CATI). In the second phase, in addition to having continued access to the web survey and CATI call-ins, study participants will be contacted through outbound CATI calls from the SOC. In the third phase, contact with study participants will be attempted through in-person locating. (Web and CATI modes will continue to be accessible throughout this phase.) Study participants who complete the survey online or by calling in to the SOC within the first four weeks will receive $40, and those who complete the survey thereafter will receive $25, irrespective of mode.
3. Analysis methods for impact estimation
Because data collection for the YCC evaluation ends in 2018, it can capture only the critical milestones that students can achieve in high school and momentum points associated with education and employment success. Collecting data on these milestones and momentum points for YCC participants and a control (RCT) or comparison (QED) group enables researchers and policymakers to gauge progress toward ultimate credential attainment and other milestones (Center for Postsecondary and Economic Success [CLASP] 2013). Ultimately, they can be used to determine which critical milestones students can achieve in high school and which momentum points might be associated with education and employment success and with eventual long-term outcomes. Because momentum points and intermediate milestones will be used as outcomes, the analyses are not defined as confirmatory or exploratory (terms that are often viewed as appropriate for describing outcomes that are final or long-term). Instead, the terms primary, secondary, and RCT impact analyses differentiate the types of analyses conducted.
Table B.1 shows the momentum points and intermediate milestones that this study will capture. Because YCC participants will be ages 16 or 17 when outcomes are measured, the focus will be on momentum points associated with credential attainment—both those that can lead to staying in and graduating from high school (the intermediate milestone) and those that will prepare students to complete postsecondary education or training. The study will also capture momentum points associated with youth gaining paid work experience, which has been associated with successful work outcomes as adults (Light 2001).
Table B.1. Momentum points associated with each milestone
. |
Education success |
Employment success |
|
. |
High school graduation/ Generalized Education Development attainment |
Postsecondary education/training completed |
Career-path employment and high wages |
Milestone in high school |
|
|
|
Momentum points |
|
|
|
The momentum points selected are associated with education and employment milestones. Predictors of dropping out of high school—Rumberger (2011) provides a synthesis—include attendance and credit accumulation (Ginsburg et al. 2014), behavior at school (Parr and Bonitz 2015), school engagement and satisfaction (Stout and Christensen 2009), and lack of involvement with the criminal justice system and substance abuse (Doll et al. 2013). Predictors of postsecondary success include standardized test scores, education expectations, passing gateway courses such as Algebra I early in high school (Hein et al. 2013), and earning postsecondary credit in high school (Lerner and Brand 2006). Predictors of paid employment for youth include both employment expectations (Acevedo et al. 2017) and work readiness skills (Al-Mamun 2012). Table B.2 shows how each momentum point and high school milestone will be empirically measured using the information from school records and the follow-up survey.
Table B.2. Outcomes used in impact analysis
|
Empirical construct |
Source |
Sample |
Analysis |
Education success |
||||
High school graduation/ GED attainment |
Binary measure of dropping out of high school by spring 2018 |
Survey |
RCT |
R |
Binary measure of whether the student graduated from high school |
School records |
QED |
S |
|
Credit accumulation |
Number of credits accumulated by spring 2018 |
School records |
QED, RCT |
P |
School attendance |
Percentage of days present in school in fall 2017 |
School records |
QED, RCT |
P |
Behavior at school |
Number of times these activities occurred in the past 3 months: late for school, cut or skipped classes, unexcused absence, got in trouble for not following school rules, was suspended or expelled |
Survey |
RCT |
R |
School engagement and satisfaction |
Participation in school-sponsored extracurricular activities in past 12 months |
Survey |
RCT |
R |
How much the student likes school |
Survey |
|||
Reduced criminal justice involvement |
Ever been arrested or taken into custody |
Survey |
RCT |
R |
Reduced substance abuse |
Drank alcohol, used marijuana, used other drugs in past month |
Survey |
RCT |
R |
Postsecondary education/training |
||||
Math proficiency |
Successful completion of Algebra I (if available) |
School records |
QED, RCT |
P |
Z-score computed from standardized tests |
P |
|||
Education expectations and knowledge |
How far student thinks he/she will get in school |
Survey |
RCT |
R |
English proficiency |
Z-score computed from standardized tests |
School records |
QED, RCT |
P |
Postsecondary credit |
Postsecondary credits achieved during high school |
Survey |
RCT |
R |
Employment success |
||||
Paid work experience |
Ever worked for pay (while in high school) |
Survey |
RCT |
R |
Employment expectations |
Expect to be working for pay full time at age 30 |
Survey |
RCT |
R |
Work readiness skills |
Working toward or obtained certificates/licenses |
Survey |
RCT |
R |
Note: Dark gray rows with bold titles show desired long-term outcomes; light gray rows without bold titles show milestones that students can achieve in high school; and rows without shading show momentum points captured in this research. The analysis column shows whether the analysis is considered primary (P), secondary (S), or RCT (R).
GED = Generalized Education Development; RCT = randomized controlled trial; QED = quasi-experimental design.
The effective capture of high school momentum points and milestones depends on whether consistent measures can be obtained across time and districts. Measures from the follow-up survey will be assessed with equal reliability because the questionnaire and survey methods will be applied consistently in each district and for each student (but will be subject to response bias). All study participants will be asked, for example, whether they have dropped out of school, and the same phrasing of the question and definition of dropping out will be used. However, measures that draw information from school records will have no such consistency because school districts do not define data elements consistently. The records often capture information using different units, intervals, or instruments, or at different times.
The following guidelines will ensure that measures that draw information at different times are consistent across districts:
Applying a common definition. When collecting information from school records, districts will provide a codebook that explains how they define each variable on the record. When definitions of a variable vary across districts, measures will be constructed to make them as consistent as possible. For example “attendance” can be defined as either students attending classes or missing entire days. Because missing the entire day is the broadest definition, when attendance data are available at the class-level only, an absent indicator will be constructed only when the student missed all classes in a day.
Constructing z-scores. Because math and English tests vary across districts and by grade, z-scores (individual score minus the mean, which is then divided by the standard deviation) will be constructed to compare proficiencies across districts. Z-scores are the recommended approach to standardizing test scores (May et al. 2009).
Standardizing the unit of measure. Some variables in school records are captured using units that have very different meanings. In such cases, the measurement will be standardized to reflect a common unit of measure. For example, as a measure of intensity of exposure to school, the number of days absent depends on the number of possible days of attendance. Therefore, this measure will be captured as a percentage of days absent or present.
Using effect sizes. The same value across some measures will have different meanings among districts or individual schools because the scale is different. For example, some districts might have a 10 percent absentee rate, whereas others might have a 40 percent rate. Reducing absenteeism by 5 percentage points has a much smaller effect in the latter than in the former. The effect size will offset scaling problems in such cases.
Handling missing data. Sensitivity analyses for alternate methods of creating the baseline covariates with missing data (for example, multiple imputation) will be performed.
Assessing baseline equivalence. When a random assignment design is conducted properly, it can be expected that there will be no systematic observable or unobservable differences between research groups except for the services offered after random assignment. However, it is still possible for differences between the two groups to exist by chance. Similarly, although the QED analysis will match YCC participants to similar nonparticipants, if participants and nonparticipants systematically differ in observable characteristics, it might not be possible to form observationally similar groups. Whether randomization and matching resulted in comparable treatment and control groups (RCT) or comparison groups (QED) will be assessed in observationally similar ways: by conducting t-tests to assess mean differences in the baseline measures of the two groups using data from the BIFs (for the RCT) and school records (for both the RCT and QED). Because parent and student BIF data were collected prior to random assignment, there should no differences in data quality or response between the treatment and control groups. Also, there should be no differences in school records data availability between treatment and comparison or control group students, because these data are systematically collected by school districts independent of the YCC evaluation. In particular, districts will record baseline data prior to random assignment, though these data will not be collected by the study team until after random assignment. To assess the joint significance of the baseline differences, t-tests on each baseline measure in isolation and a joint F-test will be used.
Addressing multiple comparisons. In a complex evaluation such as YCC, in which many comparisons are made across many outcome measures and subgroups, the probability of finding at least one apparently significant impact escalates, even if the null hypothesis of no impact for each such outcome is actually true. The basic issue is that, in the process of making multiple comparisons, there is an increased risk of falsely estimating statistically significant impacts. This problem could lead to incorrect policy decisions. At the same time, procedures that correct for multiple comparisons can lead to substantial reductions in the statistical power of hypothesis tests—the chances of identifying real differences between the contrasted groups.
The approach for addressing this problem follows the approach discussed in Schochet (2008, 2009), which involves balancing testing rigor and statistical power by differentiating among primary, secondary, and RCT impact analyses. (Table B.3 specifies which outcomes and samples will be used in each analysis.) The tests used in the primary analysis will determine the success of the YCC interventions. The primary analysis will rigorously test the study’s central hypotheses and adjust significance levels for multiple testing. It includes three primary outcomes for the impact analysis for the full sample analysis in the QED, which has considerably more statistical power than the RCT to detect program impacts. These key outcomes capture momentum points leading to educational success: school attendance, credit accumulation, and math proficiency.
The secondary impact analysis will provide preliminary information on impacts for a broader range of outcomes than are specified in the primary analysis and for all subgroup analyses. This analysis from the QED will address important study questions, useful to program stakeholders, that the primary analysis does not address. Also, it will help to (1) provide depth to the findings from the primary analysis, (2) identify new hypotheses about program effects, and (3) identify potential areas for program improvement.
Finally, the RCT impact analysis will be conducted on a still broader range of outcomes captured in the follow-up survey. This analysis will help to (1) corroborate findings from the primary analysis with a different sample and (2) identify potential hypotheses about program effects and areas for program improvement.
a. Primary impact analysis
Two strategies will be used to estimate the impact of YCC and answer the impact study research question: What is the impact of YCC on school attendance, credit accumulation, and math and English proficiency? First, simple differences in the mean values of outcomes between students in the treatment and control/comparison groups will yield an unbiased impact estimate of program effects, and the associated t-tests will assess statistical significance. Second, regression procedures that control for baseline covariates from school records (for the QED) and school records and BIFs (for the RCT) will estimate impact. This approach will improve the precision of the net-impact estimates because the covariates will explain some of the variation in outcomes, both within and between districts. In addition, covariates can adjust for the presence of any differences in observable baseline characteristics between research groups due to, for example, school assignment, random sampling, and—for survey-based analyses—interview nonresponse.
The primary analysis will use school record data to examine school attendance, credit accumulation, test scores, and (if available) successful completion of Algebra I for the QED sample. The RCT will corroborate the primary analysis with a different sample. Impacts will be estimated using the benchmark analytic model, a regression model in which an impact is calculated for each district and adjusted for students’ baseline characteristics:
(1) 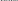 ,
,
where
 is
the outcome for student i; n is the number of
districts; Blocki,k = 1 for students
enrolled in a program at district k and 0 otherwise; YCCi
= 1 for students offered YCC entrance (treatment group) and 0
otherwise (comparison group); Xi is a vector
of measures of youths’ demographic characteristics (for
example, disability status) and prior achievement; Pk
is a vector of program characteristics; ϵ is the error
term; and βk, δk,
γi, and ηk
are the vectors of parameters to be estimated.
is
the outcome for student i; n is the number of
districts; Blocki,k = 1 for students
enrolled in a program at district k and 0 otherwise; YCCi
= 1 for students offered YCC entrance (treatment group) and 0
otherwise (comparison group); Xi is a vector
of measures of youths’ demographic characteristics (for
example, disability status) and prior achievement; Pk
is a vector of program characteristics; ϵ is the error
term; and βk, δk,
γi, and ηk
are the vectors of parameters to be estimated.
The average impact of YCC is
 .
Differences in impacts across districts can be assessed using a joint
F-test of the district-level impacts (k)
and comparing the size of the impacts. Each sample member will be
weighted equally, with differences will be explored as to whether the
results change when each district is weighted equally. Both are valid
approaches but provide slightly different estimates if districts
differ in size and have heterogeneous impacts.
.
Differences in impacts across districts can be assessed using a joint
F-test of the district-level impacts (k)
and comparing the size of the impacts. Each sample member will be
weighted equally, with differences will be explored as to whether the
results change when each district is weighted equally. Both are valid
approaches but provide slightly different estimates if districts
differ in size and have heterogeneous impacts.
The primary guide to determine whether programs have an impact is the p-value associated with the t-statistic or chi-squared statistic for the null hypothesis of no program impact on that outcome variable. The convention of reporting only treatment–comparison group differences that are statistically significant will be used. Differences significant at p < 0.05 and p < 0.01 will be made known, as will the marginally significant findings, where p < 0.10, when they contribute to a consistent pattern of impacts across multiple outcomes. The Benjamini-Hochberg method will be used to adjust for multiple comparisons for the primary outcomes.
Several additional criteria will be applied to identify potential program impacts. For example, the magnitude of the significant impact estimates will be examined to determine whether the differences are large enough to be policy relevant. Also, the sign and magnitude of the estimated impacts will be checked for similar related outcome variables in secondary and RCT impact analyses and subgroups (discussed below). In short, program effects will be identified by examining the pattern of results, rather than focusing on isolated results. Because YCC is a pilot program, it is important to see the range of potential impacts while simultaneously using rigorous criteria to interpret meaning across the outcome areas and subgroups of greatest interest.
The student- and district-level control variables included in the regression models will pertain to the period before random assignment. Variables will be selected that are correlated with key outcome measures (identified using forward stepwise regression methods with a t-statistic cutoff value of 1.0), whose mean values differ across the treatment and control/comparison groups by more than 0.25 standard deviations due to random sampling or survey nonresponse, and that are consistent with the moderating pathways suggested by the theoretical logic model for the evaluation.
The covariates for the analysis will fall into the following categories:
Youths’ demographic characteristics. These include measures of gender, race/ethnicity, low income (free and reduced-price lunch status), and English language status.
Youths’ education background. These include measures of special education status, grade level, grade point average, and credits achieved.
Program characteristics. These can include measures of program length and career pathway or strength of partnerships, level of employer engagement, intensity of work-based learning components, and small learning community (from the grantee survey).
Student-level covariates will be drawn from school records or the grantee survey and constructed as district-level covariates. Covariates will be refined on the basis of new findings or hypotheses that emerge from the implementation analysis.
When estimating impacts, the analysis will include only individuals who have non-missing values of the outcome variable. Simulations have suggested that this approach might have only a small amount of bias (0.05 standard deviations or less) when outcome data are missing at random among individuals with the same covariate values (Puma et al. 2009).
Individuals will not be excluded from the analysis if they had missing covariate values, as long as they had non-missing values of the outcome variable. For each covariate, missing values will be replaced with a placeholder value (zero) and an additional binary indicator will note whether an individual originally had a missing value for that covariate. The missing value indicator will be included in estimations. Simulations by Puma et al. (2009) have shown that this approach to handling missing covariate data is likely to keep estimation bias at less than 0.05 standard deviations.
Estimating Equation (1) will provide unbiased estimates of the impact of the opportunity to receive specific YCC services, referred to as intention-to-treat (ITT) effects. Some treatment students might not receive YCC services, however, and some control/comparison students might receive program services. (Such students are known as crossovers.) In such cases, the ITT effects will be diluted because they include the impacts of treatment group members who did not receive services and crossovers who did. The impacts using only those who participate in the program are referred to as “complier average causal effects” (CACEs). From a policy standpoint, both ITT and CACE impacts are of interest; the former provides the average impact among the target population, and the latter discloses the impact of the program on participants. An instrumental variable approach will be used to estimate impacts for the CACE parameter, replacing the YCCi indicator in Equation (1) with an indicator variable PARTi that equals 1 for those who received YCC services and 0 for those who did not, and will use treatment status as an instrumental variable for PARTi. Data from the PTS will be used to capture a minimal amount of meaningful YCC services in defining PARTi.
b. Secondary impact analysis
The secondary analysis will use school records data, the QED sample, and analyses outlined for the primary analysis to estimate impacts for (1) standardized test scores (math and English) and credit accumulation, and (2) school attendance, successful completion of Algebra I (if available), standardized test scores (math and English), and credit accumulation for different subgroups. It will answer this research question: Does the impact of YCC vary by student or program characteristics?
Three types of subgroups will be analyzed: those defined by (1) characteristics (prior academic achievement and low-income status); (2) program experience (receiving an internship, having a mentor, and completing an individual development plan, or IDP); and (3) YCC cohort (that is, year and grade in which the student started YCC). As discussed below, priority subgroup analyses will be done in areas that will allow an examination—in a new education environment and augmented program model—of prior research findings on career academies, which were similar programs found to be particularly successful among low-achieving, at-risk students (Kemple 2008). This was true of the academies when (1) they aligned career focus with employers’ needs (Greenstone and Looney 2011), (2) their students had internships and mentorships (Visher et al. 2004), and (3) they were offered as part of a small learning community (Cotton 2001). To stay focused, the study will not address additional subgroup analyses; in particular, subgroups of programs with different characteristics. Because the sample includes only 24 grantees, and because there is information in implementation only for the 10 visited, the subgroups would not contain enough districts to power the analysis, which would make finding statistically significant impacts difficult.
Subgroups defined by student characteristics. The first subgroup analysis will use baseline characteristics to determine the extent to which YCC services benefit students who were at risk of not succeeding. This analysis will answer a question that has important policy implications for targeting program services. Because studies have consistently demonstrated the strong association between past and future education performance, at-risk students could particularly benefit from YCC if program services increase motivation and skill levels, as Kemple and Snipes (2000) found was true for career academy programs. Alternatively, higher-performing students might be in a better position to use YCC services to help them continue their education or find jobs. This analysis will operationalize at-risk status using prior academic achievement, as captured by math and English test scores, and low-income, as captured by eligibility for free and reduced-price lunches. Of the 17 potential districts in the QED (of which up to 16 will be selected), 15 to 17 reported that they could provide information on academic achievement in 7th or 8th grade, and 14 reported that they could provide information on free and reduced-priced lunches.
Impacts for student subgroups defined by their prior academic achievement will be estimated by modifying Equation (1) to include terms formed by interacting subgroup indicators with the treatment status indicator and using F-tests to assess whether differences in impacts across subgroup levels are statistically significant. For example, to assess whether impacts are larger for students with lower levels of math proficiency at entrance than for those with higher levels, an indicator variable will be constructed that equals 1 for youth associated with low proficiency and 0 for youth with higher-proficiency levels. This indicator will then be interacted with the treatment status indicator and will be include it as a covariate in the regression models.
Subgroups defined by program experiences. The second set of subgroup analyses will examine impacts for subgroups defined by program experiences. Such analysis will help identify key program features that are particularly effective or ineffective. Analysis of the 2015 grantee survey showed a strong or moderate contrast between YCC and alternative programs with respect to specific types of work readiness training, job shadowing, field trips, paid internship, mentors, and IDP (Maxwell et al. 2017). Because these experiences help differentiate YCC from other programs, it is of interest to assess whether students who participate in these program components have better outcomes than students who do not. The Participant Tracking System (PTS) will assist in capturing whether YCC students in QED districts participated in an internship, had a mentor, and completed an IDP. These measures will be used to assess whether outcomes among students who received these services through YCC had improved compared to outcomes of matched students in the comparison group. Impacts for subgroups defined by program experience will be estimated using the same procedure as that for the subgroups defined by student characteristics; only the samples will vary. For example, impacts will be estimated for the sample of YCC participants who received an internship and their matched comparison group members; the YCC participants who received a mentor and their matched comparison group members; and the YCC participants who completed an IDP and their matched comparison group members.
Subgroups defined by YCC cohorts. YCC program experience can vary with the year in which the student starts the program, because more program components might be in place in later years than shortly after the grant is awarded. Building cohorts of students in the QED (Table B.2) allows use of school records to generate impact estimates for three cohorts of students. Cohort A will have entered YCC about nine months after the YCC grant awards were made; cohort B, about two years after the awards; and cohort C, about three years after the awards. Comparing impact estimates for cohorts of students in the same programs in the same schools, and using the same estimation models, will allow an assessment of whether program maturation increases the program’s impact and whether impact estimates are robust over time. In addition, because cohort A will be in a position to have graduated from high school, it will be possible to assess whether enrollment in YCC increases high school graduation rates.
c. RCT impact analysis using follow-up survey data
The RCT impact analysis will use information from the follow-up survey and the RCT sample in three districts to examine treatment–control group differences in service receipt and impacts. It will answer this research question: What appears to be the impact of YCC on school engagement and satisfaction, behavior at school, postsecondary credits earned during high school, educational expectations and knowledge, work readiness skills, paid work experiences, employment expectations, and reduced involvement with criminal justice and substance abuse?
Analysis using information from the follow-up survey changes impact estimations from Equation (1) in two ways. First, additional covariates are available from the BIFs, which enables the expansion of youth characteristics (Xi) and program characteristics (Pk) included in the estimation in Equation (1). Second, information is subject to nonresponse bias that can alter impact estimates in Equation (1) if outcomes of survey respondents and nonrespondents differ, or if the types of individuals who respond to the surveys differ across research groups. Baseline characteristics of survey respondents and nonrespondents will be used to assess whether survey nonresponse could be a problem for the follow-up survey. School records data (which will be available for the full research sample) will be used to conduct statistical tests (chi-squared and t-tests) and gauge whether, in a particular research group, those who responded to the surveys are representative of all those in that group. Noticeable differences between respondents and nonrespondents could indicate nonresponse bias.
Several approaches will be used for correcting for potential nonresponse bias. First, any observed differences between respondents will be adjusted for across the research groups using regression models. Second, because this regression procedure will not correct for differences between respondents and nonrespondents, sample weights will be constructed so that weighted observable baseline characteristics are similar for respondents and the full sample (both respondents and nonrespondents). Weights will be constructed for each research group separately, using propensity-score methods that (1) estimate a logit model predicting interview response, (2) calculate a propensity score for each individual in the full sample, and (3) construct nonresponse weights using the propensity scores. Individuals will be ranked by the size of their propensity scores and divided into several groups of equal size. The weight for a sample member will be inversely proportional to the mean propensity score of the group to which the person is assigned.
This propensity-score procedure will yield large weights for respondents with characteristics associated with low response rates (that is, for those with small propensity scores). Similarly, the procedure will yield small weights for those with characteristics associated with high response rates. Therefore, the weighted characteristics of respondents should be similar, on average, to the characteristics of the entire research sample.
i. Precision calculations of the impact estimates
Based on the approximate study sample size of 345 treatment and 195 control group members, the evaluation will have sufficient statistical power to detect meaningful impacts on key study outcomes that are similar to those that have been found in impact studies of similar types of interventions. For all study grantees, a significant impact on dropping out of school (a short-term outcome) can be expected if the true program impact is 15 percentage points or more (Table B.4); this minimum detectable impact (MDI) is larger than the rate found in an experimental evaluation of career academies (Kemple and Snipes 2000) and larger than the 12 percentage point impact found in Mathematica’s evaluation of Talent Search (Constantine et al. 2006). The MDI on achievement test scores is 0.26 standard deviations, which is similar to the 0.25 standard deviation MDI typically targeted in school-based evaluations funded by the U.S. Department of Education (WWC Procedures and Standards Handbook 2014; see p. 23 Procedures and Standards handbook).
Table B.4. Minimum detectable impacts on key outcomes
|
Minimum detectable impact (MDI) |
|
Outcome and subgroup |
Full sample |
50 percent subsample |
Dropout (percentages) |
|
|
9th- and 10th-grade students |
15.0 |
21.2 |
9th-grade students only |
18.4 |
26.0 |
Math achievement (standard deviations) |
|
|
9th- and 10th-grade students |
0.263 |
0.372 |
9th-grade students only |
0.322 |
0.455 |
|
|
|
Note: The intention-to-treat (ITT) analysis is based on the offer of YCC services. The MDI formula for the ITT estimates is as follows:
|
||
ii. Assessing and correcting for survey nonresponse bias
Parent and student BIF information will be used to assess and correct for potential survey nonresponse, which could bias the impact estimates if outcomes of survey respondents and nonrespondents differ. Two general models will assess whether survey nonresponse may be a problem for the follow-up survey:
Compare the baseline characteristics of survey respondents and nonrespondents within the treatment and control groups. Baseline data (which will be available for the full RCT research sample) will be used for statistical testing (chi-squared and t-tests) to gauge whether, in a particular research group, those who respond to the interviews are fully representative of all members of that group. Noticeable differences between respondents and nonrespondents could indicate potential nonresponse bias.
Compare the baseline characteristics of respondents across research groups. Tests for differences in the baseline characteristics of respondents across the treatment and control groups will be conducted. Statistically significant differences between respondents in different research groups could indicate potential nonresponse bias and limit the internal validity of the study if not taken into account.
Two different approaches will correct for potential nonresponse using the baseline data in estimating program impacts based on survey data. First, regression models will adjust for any observed baseline differences between respondents across all research groups. Second, because this regression procedure will not correct for differences between respondents and nonrespondents, sample weights will be constructed so that weighted observable baseline characteristics are similar for respondents and for the full sample (both respondents and nonrespondents). Weights will be constructed separately for each research group, using the following three steps:
Estimate a logit model predicting interview response that regresses the binary variable indicating whether a sample member is a respondent to the instrument on baseline measures.
Calculate a propensity score for each individual in the full sample for the predicted probability that a sample member is a respondent, using the parameter estimates from the logit regression model and the person’s baseline characteristics. Individuals with large propensity scores are likely to be respondents, whereas those with small propensity scores are likely to be nonrespondents.
Construct nonresponse weights using the propensity scores. Individuals will be ranked by the size of their propensity scores and divided into several groups of equal size. The weight for a sample member will be inversely proportional to the mean score of the group to which the person is assigned. This method will ensure that no individual has a very low or a very high weight, which would lead to less precise estimates.
This propensity score procedure will yield large weights for survey respondents who have characteristics associated with low response rates (that is, those with small propensity scores). Similarly, the procedure will yield small weights for respondents who have characteristics that are associated with high response rates. Thus, the weighted characteristics of respondents should be similar, on average, to the characteristics of the entire research sample.
Finally, for key outcomes, multiple imputation methods (using Stata’s multiple imputation commands) will correct for nonresponse using the sensitivity of the results to alternative methods will be used to adjust for survey nonresponse. Rubin (1987, 1996) and Shafer (1997) discuss the theory underlying multiple imputation procedures.
Assessing and correcting for district nonparticipation. During the recruitment process, data on key district characteristics was obtained. This information will be used to compare the characteristics of the selected districts that participated in the impact study (both the RCT and QED) to those that did not, which helps in interpreting the analysis findings. However, because districts were not randomly selected for inclusion but instead selected based on suitability for the study, results obtained from participating districts will not be generalizable to a well-defined universe of districts. Consequently, the benchmark approach will not adjust the impact estimates for district nonparticipation, because the study is not designed to achieve external validity. However, sensitivity analyses will be conducted that use district-level nonresponse weights constructed using similar propensity score methods to those described above.
Assessing and correcting for sample exclusion with missing baseline or outcome data. The QED analysis requires non-missing baseline data in order to match YCC participants to observationally similar nonparticipants, and non-missing outcome data to determine the impact of YCC. The sample of YCC participants and potential matches will therefore be restricted to those students who have both baseline data and outcome data. It is assumed that 87 percent of YCC participants will have non-missing data for all covariates used to match students and for all outcome data. Because the pool of potential matches in each district is much larger than the pool of YCC participants, matches to each participant should be possible, even when restricting matches to treatment group participants with non-missing data to a nonparticipant with non-missing data.
4. Methods to maximize response rates and data reliability
This study is requesting approval for (1) the use of a parental consent form to be completed in one district in the RCT before the follow-up survey is administered and (2) a follow-up survey for three districts in the RCT. Depending on when the survey is completed, respondents will be eligible for an incentive of $40 or $25. There is no incentive for the parental consent form.
The methods to maximize response rates and data reliability are discussed first for the parental consent form and follow-up survey and then for the student records data collection.
Response rates. An 80 percent response rate for the follow-up survey is expected. The data collection strategy uses practices that have been successful with similar populations. The strategy’s key aspects include multiple modes to maximize flexibility, early identification of barriers to response, and an “early bird” incentive strategy.
A multimode approach utilizes three phases of data collection. In the first phase, study participants will be directed to the web survey or to call in to Mathematica’s SOC to complete the survey using CATI. In the second phase, in addition to continued access to the web survey and CATI call-ins, study participants will be contacted through outbound CATI calls from the SOC. In the third phase, contact with study participants will be attempted through in-person locating. (The web and CATI modes will continue to be accessible throughout this phase.) This approach will maximize efficiency by encouraging early survey completion using the modes that require the least amount of resources (web and CATI call-ins) before moving to modes requiring increased interviewer labor (CATI call-outs and field locating). This approach provides flexibility and maximizes response by accommodating participants who prefer to self-administer the survey. Additionally, this approach allows for response by study participants who do not have access to the Internet or do not have listed phone numbers. To further increase access, all respondents will be able to complete the web survey in Spanish or by using CATI with a trained, bilingual interviewer.
Multiple outreach and locating strategies will further encourage and address potential barriers to response. Study participants will receive key information about the evaluation in the advance letter and in multiple rounds of reminder letters using various modes, including mail and email. In addition, permission to contact study participants via SMS text messaging was collected at the time of sample enrollment. Because youth are more likely to have a stable Internet presence than a physical address, social media contact information (such as Facebook, Twitter, and Instagram) will be collected and used throughout the follow-up fielding period’s locating efforts. Planned in-person locating efforts will focus on study participants who do not have a published phone number and cannot be contacted through other means.
Another strategy for maximizing response is the incentive structure, by which study participants who complete their survey online or by calling in to the SOC within the first four weeks will receive $40, and those who complete the survey thereafter will receive $25, irrespective of how they complete the survey. The emphasis on survey completion during the first four-week phase of the survey fielding period will limit the project resources needed to contact study participants later in the data collection period, as well as reduce the number of outreach attempts experienced by study participants.
Data reliability. The follow-up survey instrument has been reviewed by staff at DOL, project team members, and representatives from YCC programs. It has been thoroughly pre-tested with a group of students similar to those in the follow-up sample. As another assurance of data reliability, telephone interviewers and field locators will receive extensive training in administering the instrument and identifying potential barriers to response. This training will also focus on ensuring cooperation of those in the control group, who, because they were not selected for enrollment in the program, may be less inclined than treatment group members to participate.
Monitoring and validation will also be critical to data reliability. Mathematica employs a standard of monitoring 10 percent of the hours each interviewer spends interacting with sample members and administering interviews. Also, 10 percent of completed surveys generated from the field locators will be subject to field validation to ensure that the correct participant was contacted and that the locator met all expectations of professionalism and data collection best practices.
5. Tests of procedures or methods
Pre-testing a survey is critical to the integrity of a data collection. Because the parental consent form will include language similar to that used in the baseline parental consent form, challenges in administering it will be minimal. The follow-up survey uses questions from the BIFs, as well as from other studies of similar populations, to ensure that items are worded simply and clearly, that the information being requested is reasonable to ask from youth, that response categories are clear, that questions have clear instructions, and that the questions are within the reading level range of the target population.
For the pre-test, five students provided feedback on the survey questions. Some students were participating in YCC but were not part of the follow-up sample; others were not participating in YCC and were similar to those in the control group. These students completed a self-administered version of the questionnaire, followed by a respondent debriefing to assess comprehension, clarity of instructions, skip logic concerns, and overall survey flow. In addition, students were asked about the timing of the survey and the ease of administration. Findings from these pre-tests can be found in the accompanying pretest results memo.
6. Consultants on statistical methods
Consultations on the statistical methods used in this study have been done to ensure the technical soundness of the study. The following people consulted on statistical aspects of the design and will be primarily responsible for collecting and analyzing the data for the agency:
Mathematica Policy Research
Dr. Peter Schochet (609) 936-2783
Dr. Nan Maxwell (510) 830-3726
Ms. Jeanne Bellotti (609) 275-2243
REFERENCES
Acevedo, Paloma, Guillermo Cruces, Paul Gertler, and Sebastian Martinez. “Living Up to Expectations: How Job Training Made Women Better Off and Men Worse Off.” NBER Working Paper No. 23264. Cambridge, MA: National Bureau of Economic Research, March 2017. Available at http://www.nber.org/papers/w23264. Accessed September 3, 2017.
Al-Mamun, Abdullah. “The Soft Skills Education for the Vocational Graduate: Value as Work Readiness Skills.” British Journal of Education, Society & Behavioural Science, vol. 2, no. 4, 2012, pp. 326–338.
Center for Postsecondary and Economic Success at CLASP. “A Framework for Measuring Career Pathways Innovation: A Working Paper.” The Alliance for Quality Career Pathways. February 2013. Available at http://www.clasp.org/resources-and-publications/publication-1/CLASP-AQCP-Metrics-Feb-2013.pdf. Accessed September 3, 2017.
Constantine, Jill, Neil Seftor, Emily Sama Martin, Tim Silva, and David Myers. “A Study of the Effect of Talent Search on Secondary and Postsecondary Outcomes in Florida, Indiana, and Texas: Final Report from Phase II of the National Evaluation.” Washington, DC: U.S. Department of Education, Office of Planning, Evaluation and Policy Development, Policy and Program Studies Service, 2006. Available at https://www2.ed.gov/rschstat/eval/highered/talentsearch-outcomes/ts-report.pdf. Accessed September 3, 2017.
Cotton, Kathleen. “New Small Learning Communities: Findings from Recent Literature.” Washington, DC: U.S. Department of Education, Office of Educational Research and Improvement, 2001. Available at http://files.eric.ed.gov/fulltext/ED459539.pdf. Accessed September 25, 2017.
Doll, Jonathan Jacob, Zohreh Eslami, and Lynne Walters. “Understanding Why Students Drop Out of High School, According to Their Own Reports: Are They Pushed or Pulled, or Do They Fall Out? A Comparative Analysis of Seven Nationally Representative Studies.” Sage Open, vol. 3, no. 4, October-December 2013, pp. 1–15. Available at http://journals.sagepub.com/doi/pdf/10.1177/2158244013503834. Accessed September 3, 2017.
Ginsburg, Alan, Phyllis Jordan, and Hedy Chang. “Absences Add Up: How School Attendance Influences Student Success.” Attendance Works, August 2014. Available at http://www.attendanceworks.org/wordpress/wp-content/uploads/2014/09/Absenses-Add-Up_September-3rd-2014.pdf. Accessed September 3, 2017.
Greenstone, Michael, and Adam Looney. “Building America’s Job Skills with Effective Workforce Programs: A Training Strategy to Raise Wages and Increase Work Opportunities.” Washington DC: Brookings Institution, November 2011. Available at https://www.brookings.edu/research/building-americas-job-skills-with-effective-workforce-programs-a-training-strategy-to-raise-wages-and-increase-work-opportunities/. Accessed September 3, 2017.
Kemple, James J. “Career Academies: Long-Term Impacts on Labor Market Outcomes, Educational Attainment, and Transitions to Adulthood.” New York, NY: MDRC, June 2008. Available at http://www.mdrc.org/sites/default/files/full_50.pdf. Accessed September 3, 2017.
Kemple, James J., and Jason C. Snipes. “Career Academies: Impacts on Students’ Engagement and Performance in High School.” New York, NY: MDRC, March 2000. Available at http://www.mdrc.org/sites/default/files/full_45.pdf. Accessed September 3, 2017.
Lerner, Jennifer Brown, and Betsy Brand. “The College Ladder: Linking Secondary and Postsecondary Education for Success for All Students.” Washington, DC: American Youth Policy Forum, September 2006. Available at http://www.aypf.org/publications/The%20College%20Ladder/TheCollegeLadderlinkingsecondaryandpostsecondaryeducation.pdf. Accessed September 3, 2017.
Light, Audrey. “In School Work Experience and the Returns to Schooling.” Journal of Labor Economics, vol. 19, no. 1, January 2001, pp. 65–93.
May, Henry, Irma Perez-Johnson, Joshua Haimson, Samina Sattar, and Phil Gleason. “Using State Tests in Education Experiments: A Discussion of the Issues.” NCEE 2009-013. Washington, DC: U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, November 30, 2009. Available at https://www.mathematica-mpr.com/our-publications-and-findings/publications/using-state-tests-in-education-experiments-a-discussion-of-the-issues. Accessed September 3, 2017.
Maxwell, Nan L., Emilyn Whitesell, Jeanne Bellotti, Sengsouvanh (Sukey) Leshnick, Jennifer Henderson-Frakes, and Daniela Berman. “Youth CareerConnect: Early Implementation Findings.” Princeton, NJ: Mathematica Policy Research, April 2017. [Draft submitted to DOL]
Parr, Alyssa K., and Verena S. Bonitz. “Role of Family Background, Student Behaviors, and School-Related Beliefs in Predicting High School Dropout.” The Journal of Educational Research, vol. 108, no. 6, September 2015, pp. 504–514.
Puma, Michael J., Robert B. Olsen, Stephen J. Bell, and Cristofer Price. “What to Do When Data Are Missing in Group Randomized Controlled Trials.” NCEE 2009-0049. Washington, DC: National Center for Education Evaluation and Regional Assistance, October 2009. Available at http://files.eric.ed.gov/fulltext/ED511781.pdf. Accessed September 3, 2017.
Rubin, D.B. Multiple Imputation for Nonresponse in Surveys. New York: J. Wiley & Sons, 1987.
Rubin, D.B. (1996) Multiple imputation after 18+ years (with discussion). Journal of the American Statistical Association, 91, 473-489.
Rumberger, Russell W. Dropping Out: Why Students Drop Out of High School and What Can Be Done About It. Cambridge, MA: Harvard University Press, 2011.
Schafer, J.L. Analysis of Incomplete Multivariate Data. London: Chapman & Hall, 1997.
Schochet, Peter Z. “An Approach for Addressing the Multiple Testing Problem in Social Policy Impact Evaluations.” Evaluation Review, vol. 33, no. 6, December 2009, pp. 539–567.
Schochet, Peter Z. “Statistical Power for Random Assignment Evaluations of Education Programs.” Journal of Educational and Behavioral Statistics, vol. 33, no. 1, March 2008, pp. 62–87.
Stout, Karen E., and Sandra L. Christenson. “Staying on Track for High School Graduation: Promoting Student Engagement.” The Prevention Researcher¸ vol. 16, no. 3, September 2009, pp. 17–20.
Visher, Mary G., Rajika Bhandari, and Elliott Medrich. “High School Career Exploration Programs: Do They Work?” Phi Delta Kappan, vol. 86, no. 2, October 2004, pp. 135–138.
What Works Clearinghouse. Procedures and Standards Handbook, Version 3.0. March 2014. Available at https://ies.ed.gov/ncee/wwc/Docs/referenceresources/wwc_procedures_v3_0_standards_handbook.pdf. Accessed September 3, 2017.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Alicia Harrington |
| File Modified | 0000-00-00 |
| File Created | 2021-01-21 |
© 2026 OMB.report | Privacy Policy
 where
where
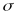 is the standard deviation of the outcome measure,
is the standard deviation of the outcome measure,
 is the survey or school records response rate,
is the survey or school records response rate,
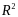 is the explanatory power of regression variables, and
is the explanatory power of regression variables, and
 and
and
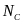 are sample sizes for the treatment and control groups,
respectively (see Schochet 2008). Analysis of data from similar
populations suggests r
= 0.80 for the
survey outcomes (dropout) and r
= 0.87 for the
outcomes based on school records data (math achievement).
are sample sizes for the treatment and control groups,
respectively (see Schochet 2008). Analysis of data from similar
populations suggests r
= 0.80 for the
survey outcomes (dropout) and r
= 0.87 for the
outcomes based on school records data (math achievement).
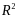 is set to 0.2 for the dropout rate and 0.5 for the academic
achievement test based on previous experience. The MDI
calculations assume a two-tailed test with 80 percent power and a
5 percent significance level, yielding a factor of 2.80 in the
MDI formula.
is set to 0.2 for the dropout rate and 0.5 for the academic
achievement test based on previous experience. The MDI
calculations assume a two-tailed test with 80 percent power and a
5 percent significance level, yielding a factor of 2.80 in the
MDI formula.