Attachment B Experimental Design
Attachment B Experimental Design 20170628.docx
Risk Preferences and Demand for Crop Insurance and Cover Crop Programs (RPDCICCP)
Attachment B Experimental Design
OMB: 0536-0076
Attachment B
Experimental Design Protocol
Overview
Key Design Terminology
Experiment – The experiment is composed of multiple 90-minute sessions. The number of sessions in an experiment is determined by the size of the laboratory facility, the budget for the project, and the statistical power required to test the primary research hypotheses.
Session – A session involves a number of individual participants who make decisions independently of each other. The session starts when we open the doors of the lab and ends 90 minutes later. The number of participants may vary across sessions, and is capped by the size of the laboratory facility (25 students maximum).
Section – Each session consists of 4 sections: 3 elicitation tasks, and a demographic questionnaire. All subjects complete all sections of the session.
Elicitation Task – An elicitation task, for the purposes of this experiment, is a set of incentivized decisions that each subject completes in order to measure a specific innate characteristic of the subject. Our experiment involves three elicitation tasks: a task to measure Cumulative Prospect Theory (CPT) risk preferences, a task to measure Myopic Loss Aversion (MLA) risk preferences, and a task to measure insurance and cover crop demand elasticities.
Payment level and payoff state – In the cumulative prospect theory elicitation task, subjects will be asked to choose between risky options. Examples of risky options include:
A lottery that pays $4.00 half of the time and $1.00 for the other half of the time.
A lottery that pays $15.00 two out of 10 times and $0.00 for the remaining 8 out of 10 times.
A lottery that pays $25 if two coin flips in a row are both heads, $10 if two coin flips in a row are ordered heads then tails, $10 if two coin flips in a row are ordered tails then heads, and $0 if two coin flips in a row are both tails.
The payment level is the amount of money that the lottery pays out, and the payoff state is the number of possible payment levels. For example 1 above, there are two payment levels: $4.00 or $1.00. The payoff state is the number of possible payment levels, which is 2 in this case. For example 3 above, there are three possible payment levels ($25, $10, $0) but four possible payoff states (heads heads, heads tails, tails heads, tails tails).
Round – Each elicitation task will involve multiple rounds. In each round, a subject is asked to make one or more decisions in response to a risky outcome. Specific variables are changed between rounds according to the needs of the elicitation task. For the prospect theory risk elicitation task, the scale or framing of the risk changes between rounds. For the myopic risk elicitation task, the time commitment of decisions changes between rounds. For the demand elicitation task, prices are changed between rounds. More rounds per elicitation task improve the statistical power of the task to measure an individual subject’s characteristics given underlying population heterogeneities.
Treatment – A treatment, for the purposes of this experiment, is the environment in which subjects make their decisions for the myopic risk elicitation task and the demand elicitation task. The environment specifies a particular distribution of revenue risk that each subject faces individually. The risk environment provides context for subjects’ decisions about purchasing insurance and/or investing in cover crops. The experiment will include four different risk environment treatments. Each subject will participate in only one treatment.
Stage – In the experimental instructions and procedures, rounds are referred to as stages. Rounds are ordered within a specific elicitation task. Stages are ordered with reference to the first round of the first elicitation task in the experiment. This change of terminology facilitates subjects in tracking their own progress across the various sections of the experiment.
Revenue – Revenue is the money that subjects’ earn from their decisions in the experiment. The risk environment treatments impact the amount of revenue risk experienced by each subject during the experiment.
Experiment Structure
Computer-based tasks implemented in Python with internet administration
Maximum of 500 students subjects recruited at the University of Rhode Island
Each subject completes three elicitation tasks: a prospect theory risk preferences task, a myopic risk preferences task, and demand elasticities task. Each subject also completes a short demographic questionnaire
The experiment will take no more than 90 minutes to complete. The order of events in the experiment is:
Welcome, signing of consent forms
Instructions
Cumulative Prospect Theory elicitation task
Myopic Loss Aversion elicitation task
Insurance and cover crop demand elasticities task
Demographic questionnaire
Final payments
The prospect theory task will be the same for all subjects. The myopic and demand tasks will be different across subjects depending on which risk environment treatment the subject is assigned to.
There will be four risk environment treatments:
High expected revenue, high revenue variance – In this treatment, revenues will be drawn from the set [0, 5, 10, 15, 20, 25, 30] where each outcome has equal probability of occurring.
Low expected revenue, high revenue variance – In this treatment, revenues will be drawn from the set [0, 4, 8, 12, 16, 20, 24] where each outcome has equal probability of occurring.
High expected revenue, low revenue variance – – In this treatment, revenues will be drawn from the set [5, 8.33, 11.67, 15, 18.33, 21.67, 25] where each outcome has equal probability of occurring.
Low expected revenue, low revenue variance – – In this treatment, revenues will be drawn from the set [4, 6.67, 9.33, 12, 14.67, 17.33, 20] where each outcome has equal probability of occurring.
Subjects will be evenly allocated among environment treatments. Each subject will make decisions within a single, randomly assigned risk environment treatment for both the myopic and demand tasks.
Elicitation Tasks
The experiment has three different elicitation tasks.
Cumulative Prospect Theory risk elicitation task. The CPT risk elicitation task will have 20 rounds. For each round, subjects will make 10 decisions. Each decision will involve two options: A and B. In all rounds, option A will involve a risky choice. In some rounds, option B will involve a risky choice while in other rounds the choice will be a certain outcome. For each round and each decision, subjects will choose either A or B.
Figure 1 shows the first nine rows of an example round. In this example, option A always pays $4.00 if bingo balls 1-3 are drawn, and $1.00 if bingo balls 4-10 are drawn. The expected value of option A is $1.90 for all rows. Option B changes in each row. In the first row, option B pays $4.00 if bingo ball 1 is drawn, and $0.50 if bingo balls 2-10 are drawn. In each subsequent row, the probabilities are unchanged, but the payoffs increase. In the last row of this menu (not displayed in Figure 1), option B pays $60.20 if bingo ball 1 is drawn and $1.00 if bingo balls 2-10 are drawn.
The data recorded for each round is the row in which a subject changes from preferring option A to option B. In Figure 1, this occurs in row 6.
In each round, the sets of options A and B change. Across rounds, the sets of options A and B may vary by:
Payment levels – In Figure 1, the payment levels are $4.00 and $1.00 for option A in every row. Payment levels for option A and/or option B may change across rounds, and across rows within a given round. The minimum possible payment across all rounds is -$4.501, and the maximum possible payment is $100.00.
Payment probabilities – In Figure 1, the payment probabilities are 0.3 and 0.7 for option A in every row. Payment probabilities for option A and/or option B may change across rounds.
Number of payoff states – In Figure 1, there are only two possible payoff states (drawing either 1-3 or drawing 4-10) for option A in every row. Across all rounds, option A ranges from two possible payoff states per row to four possible payoff states per row. Option B ranges from one possible payoff state per row (a certain outcome) to a maximum of two possible payoff states per row.
Payment scaling – In Figure 1, the payment levels for option B increase at an increasing rate from the first row to the last row in the menu. Across all rounds, some menus keep a constant payment jump across rows (referred to as a linear payment scale) and other menus increase the payment jumps across rows at a constant rate (referred to as a power payment scale).
Table 1 summarizes the main parameters for each round of the CPT risk elicitation task. The menu shown in Figure 1 is for illustrative purposes only and does not correspond to any of the rows in Table 1.
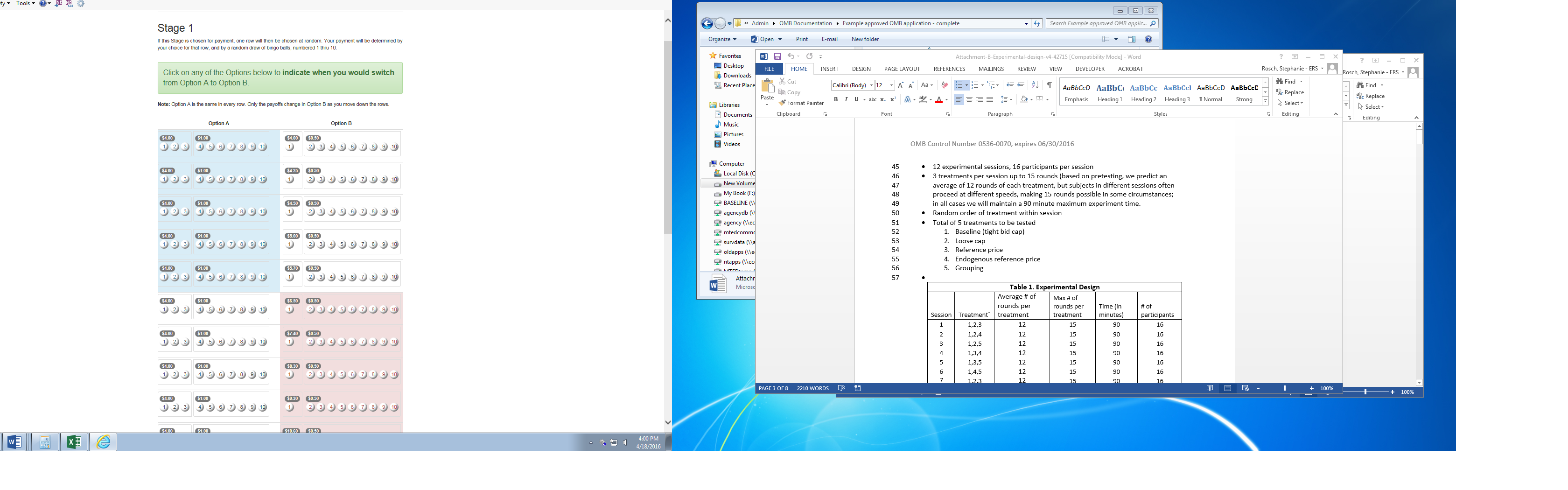
Figure 1: Screenshot of Portion of the Round 1 Menu in CPT Risk Elicitation Task (displays only first 9 rows of the full menu)
Table 1: Summary of Parameter Variation across Rounds for CPT Risk Elicitation Task
Round |
Payment Scaling |
First Row |
Last Row |
||
Option A |
Option B |
Option A |
Option B |
||
1 |
Power |
$4.00 Prob = .3 $1.00 Prob = .7 |
$5.30 Prob = .1 $0.50 Prob = .9 |
$4.00 Prob = .3 $1.00 Prob = .7 |
$60.20 Prob = .1 $0.50 Prob = .9 |
2 |
Power |
$4.00 Prob = .9 $3.00 Prob = .1 |
$4.44 Prob = .7 $0.50 Prob = .3 |
$4.00 Prob = .9 $3.00 Prob = .1 |
$16.14 Prob = .7 $0.50 Prob = .3 |
3 |
Linear |
$2.85 Prob = .5 -$0.40 Prob = .5 |
$3.00 Prob = .5 -$2.10 Prob = .5 |
$0.15 Prob = .5 -$0.80 Prob = .5 |
$3.00 Prob = .5 -$2.10 Prob = .5 |
4 |
Power |
$10.00 Prob = .2 $2.50 Prob = .8 |
$12.42 Prob = .1 $1.00 Prob = .9 |
$10.00 Prob = .2 $2.50 Prob = .8 |
$100.00 Prob = .1 $1.00 Prob = .9 |
5 |
Linear |
$5.23 Prob = .5 $0.00 Prob = .5 |
$5.50 Prob = .5 -$3.00 Prob = .5 |
$0.27 Prob = .5 -$0.40 Prob = .5 |
$5.50 Prob = .5 -$0.40 Prob = .5 |
6 |
Power |
$6.00 Prob = .9 $0.00 Prob = .1 |
$6.64 Prob = .6 $1.00 Prob = .4 |
$6.00 Prob = .9 $0.00 Prob = .1 |
$23.74 Prob = .6 $1.00 Prob = .4 |
7 |
Linear |
$6.18 Prob = .6 $0.00 Prob = .4 |
$6.50 Prob = .5 -$4.50 Prob = .5 |
$0.33 Prob = .6 $0.00 Prob = .4 |
$6.50 Prob = .5 $0.00 Prob = .5 |
8 |
Power |
$15.00 Prob = .2 $1.00 Prob = .8 |
$17.21 Prob = .1 -$1.00 Prob = .9 |
$15.00 Prob = .2 $1.00 Prob = .8 |
$82.91 Prob = .1 -$1.00 Prob = .9 |
9 |
Power |
$8.00 Prob = .9 $0.00 Prob = .1 |
$9.20 Prob = .6 -$2.00 Prob = .4 |
$8.00 Prob = .9 $0.00 Prob = .1 |
$45.20 Prob = .6 -$2.00 Prob = .4 |
10 |
Linear |
$25.00 Prob = .5 $0.00 Prob = .5 |
$1.25 Prob = 1 |
$25.00 Prob = .5 $0.00 Prob = .5 |
$23.75 Prob = 1 |
11 |
Linear |
$25.00 Prob = .5 $0.00 Prob = .5 |
$2.27 Prob = 1 |
$25.00 Prob = .5 $0.00 Prob = .5 |
$22.73 Prob = 1 |
12 |
Power |
$75.00 Prob = .2 $0.00 Prob = .8 |
$1.91 Prob = 1 |
$75.00 Prob = .2 $0.00 Prob = .8 |
$68.51 Prob = 1 |
13 |
Power |
$100.00 Prob = .2 $0.00 Prob = .8 |
$3.40 Prob = 1 |
$100.00 Prob = .2 $0.00 Prob = .8 |
$91.60 Prob = 1 |
14 |
Power |
$33.00 Prob = .33 $0.00 Prob = .67 |
$0.58 Prob = 1 |
$33.00 Prob = .33 $0.00 Prob = .67 |
$30.06 Prob = 1 |
15 |
Linear |
$7.60 Prob = .5 $0.00 Prob = .5 |
$8.00 Prob = .4 -$4.50 Prob = .6 |
$0.40 Prob = .5 $0.00 Prob = .5 |
$8.00 Prob = .4 $0.00 Prob = .6 |
16 |
Power |
$8.00 Prob = .3 $3.00 Prob = .7 |
$10.16 Prob = .1 $0.00 Prob = .9 |
$8.00 Prob = .3 $3.00 Prob = .7 |
$92.96 Prob = .1 $0.00 Prob = .9 |
17 |
Linear |
$50.00 Prob = .25 $25.00 Prob = .50 $0.00 Prob = .25 |
$2.50 Prob = 1 |
$50.00 Prob = .25 $25.00 Prob = .50 $0.00 Prob = .25 |
$47.50 Prob = 1 |
18 |
Linear |
$33.00 Prob = .67 $0.00 Prob = .33 |
$1.65 Prob = 1 |
$33.00 Prob = .67 $0.00 Prob = .33 |
$31.35 Prob = 1 |
19 |
Linear |
$66.00 Prob = .44 $33.00 Prob = .44 $0.00 Prob = .11 |
$3.30 Prob = 1 |
$66.00 Prob = .44 $33.00 Prob = .44 $0.00 Prob = .11 |
$62.70 Prob = 1 |
20 |
Linear |
$50.00 Prob = .25 $25.00 Prob = .50 $0.00 Prob = .25 |
$2.50 Prob = 1 |
$50.00 Prob = .25 $25.00 Prob = .50 $0.00 Prob = .25 |
$47.50 Prob = 1 |
The data output from this task will be a set of 20 switching points for each subject – one switching point per round. This output will be used to estimate parameters for a prospect theory model of individual risk preferences. These parameters will be correlated with demographic characteristics and outputs from the other two elicitation tasks.
Myopic Loss Aversion risk elicitation task. The myopic loss aversion elicitation task will have 30 rounds. For half of the rounds, subjects will make a decision in each round. For the other half of this tasks, subjects will make a decision once every five rounds.
In each round, subjects will be faced with a risky baseline revenue distribution. The actual distribution will vary across subjects depending on which environmental treatment they are assigned to. In each round, subjects will make a decision about purchasing insurance for their revenue risk. Insurance will guarantee a minimum level of revenue for the period.
The level of coverage and purchase price will be drawn randomly each round. The set of coverage options to draw from is {20%, 25%, 30%, 45%, 50%, 55%}. Coverage is measured as percent loss from expected revenue. The range of coverage options in the experiment mirrors real-world crop insurance levels for catastrophic and shallow loss insurance programs. Prices incorporate a subsidy rate drawn from the set: {0.3, 0.4, 0.5, 0.75, 1, 1.25, 1.5, 2}. Subsidy rates are measured as multipliers on the actuarially fair rate, where subsidy = 1 correspond to the actuarially fair insurance price. The range of prices includes subsidy rates similar to real-world crop insurance programs as well as rates comparable to commercially available insurance.
The data output from this task will be a set of individual-level insurance purchase decisions conditional on coverage level, price (subsidy), risk environment, and decision frequency. This output will be used to estimate individual-specific demand elasticities for insurance. These demand elasticities will be correlated with demographic characteristics and parameter estimates from the prospect theory task. Demand elasticities will also be used to statistically test for average differences across environmental treatments.
Insurance and cover crop demand elicitation task. The insurance and cover crop demand elicitation task will have 15 rounds. Subjects will make a decision in each round.
In each round, subjects will be faced with a risky baseline revenue distribution. The actual distribution will vary across subjects depending on which environmental treatment they are assigned to. In each round, subjects will make decisions about purchasing either of two risk management options: insurance and/or a cover crop investment. The insurance option will be implemented in exactly the same manner as for the myopic task.
The cover crop investment will change the baseline revenue risk distribution to reduce the expected variance of revenue. Baseline revenue distributions are uniform in all treatments. The cover crop investment will change the revenue distribution to be more like a triangular distribution. Table 2 summarizes the changes to the revenue distribution with the cover crop investment. The middle outcome will be drawn with probability 0.3. The outcome immediately above and below the middle outcome will be drawn with probability 0.2. The outcomes two above and below the middle outcome will be drawn with probability 0.1. The most extreme outcomes above and below the middle outcome will be drawn with probability 0.05.
Table 2: Changes to Revenue Distribution with Cover Crop Investment (All Treatments)
Outcome |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Frequency under Baseline Distribution |
0.143 |
0.143 |
0.143 |
0.143 |
0.143 |
0.143 |
0.143 |
Frequency under Cover Crop Investment |
0.05 |
0.1 |
0.2 |
0.3 |
0.2 |
0.1 |
0.05 |
There will be only a single level to cover crop investment, however prices will be drawn randomly with the same range of subsidy rates as the insurance option.
The data output from this task will be a set of individual-level insurance and cover crop purchase decisions conditional on insurance coverage level, insurance price, cover crop price, and risk environment. This output will be used to estimate individual-specific demand elasticities for insurance and cover crops. These demand elasticities will be correlated with demographic characteristics and parameter estimates from the CPT elicitation task. Demand elasticities will also be used to statistically test for average differences across environmental treatments, as well as for individual differences in insurance demand elasticities between the myopic and demand tasks.
Payments
Payment procedures. Subjects will receive a show-up fee consistent with standard practice at the University of Rhode Island’s SimLab. They will receive this payment even if they decline to participate in the experiment. Subjects will also receive compensation based on the decisions they make during the course of the experiment, if they decide to participate.
Each subject will be randomly assigned to one of four possible risk environments. Within their assigned risk environment treatment, each subject will complete multiple rounds of three different tasks: 20 rounds of CPT risk elicitation task, 30 rounds of the MLA risk elicitation task, and 15 rounds of the insurance and cover crop demand elicitation task. Each round of each task will require a subject to evaluate one or more risky decisions. Each subject will complete all 65 rounds within a 90 minute time period.
When all rounds of all tasks are completed, one round will be randomly selected for payment from the entire experiment. Subjects will receive a cash payment based on the decision in that specific round. For rounds that involve multiple risky decisions, a single decision from the round will be selected for payment.
Show-up fee. The show-up fee for this experiment will be $10.
Distribution of Payments. The expected payment for this experiment, including show-up fee, is between $20-25, depending on the risk environment treatment. The maximum possible payment, in all treatments, is $100 plus the show up fee.
Table 3 shows the expected payment, range of payments, and probability of receiving a high payment (conditional on selection) for each round of the experiment. Each round has an equal probability of being selected for payment. Out of 65 total rounds, 9 rounds have maximum payments of $50 - $100, and 5 rounds have maximum payments of $75 - 100. Therefore the probability of selecting any round where the maximum payment can exceed $50 is 9/65 = 13.85% and the probability of selecting any round where the maximum payment can exceed $75 is 5/65 = 7.69%.
Table 3: Range of Payments Possible for Each Round of the Experiment (All Treatments)
Round |
Expected Payment |
Min Possible Payment |
Max Possible Payment |
Within Round Probability of Payment ≥ $50 |
Within Round Probability of Payment ≥ $75 |
1 |
$3.46 |
$0.50 |
$60.20 |
2% |
|
2 |
$7.04 |
$0.50 |
$16.14 |
|
|
3 |
$0.67 |
-$2.10 |
$3.00 |
|
|
4 |
$6.30 |
$1.00 |
$100.00 |
5% |
2% |
5 |
$2.18 |
-$3.00 |
$5.50 |
|
|
6 |
$9.17 |
$0.00 |
$23.74 |
|
|
7 |
$2.84 |
-$4.50 |
$6.50 |
|
|
8 |
$4.68 |
-$1.00 |
$82.91 |
4% |
1% |
9 |
$14.65 |
-$2.00 |
$45.20 |
|
|
10 |
$15.63 |
$0.00 |
$25.00 |
|
|
11 |
$15.34 |
$0.00 |
$25.00 |
|
|
12 |
$31.31 |
$0.00 |
$75.00 |
20% |
20% |
13 |
$42.36 |
$0.00 |
$100.00 |
20% |
20% |
14 |
$15.60 |
$0.00 |
$33.00 |
|
|
15 |
$2.80 |
-$4.50 |
$8.00 |
|
|
16 |
$5.67 |
$0.00 |
$92.96 |
4% |
2% |
17 |
$31.25 |
$0.00 |
$50.00 |
25% |
|
18 |
$23.82 |
$0.00 |
$33.00 |
|
|
19 |
$47.63 |
$0.00 |
$66.00 |
44% |
|
20 |
$31.25 |
$0.00 |
$50.00 |
25% |
|
21-50* |
$12 or $15 |
$0, $4, or $5 |
$20, $24, $25, or $30 |
|
|
51-65* |
$12 or $15 |
$0, $4, or $5 |
$20, $24, $25, or $30 |
|
|
* For these rounds, payment parameters depend on the environmental treatment. Environmental treatments specify payments ranges as either $0-$30, $0-$24, $4-$20, or $5-$25.
Because few rounds have possible payments above $50 and the probabilities of drawing a high payment are also low within those particular rounds, the overall likelihood of earning payments above $50 is low for the full experiment. Conditional on selection, the total probability of realizing a payoff of $100 is (1/65)*(0.05 + 0.20) = 0.385%. The probability of realizing a payoff of greater than $75 conditional on selection is (1/65)*(0.02 + 0.01 + 0.2 + .2 + 0.02) = 0.692%. The probability of realizing a payoff greater than $50 conditional on selection is (1/65)*(0.02 + 0.05 + 0.04 + 0.2 + 0.2 + 0.04 + 0.25 + 0.44 + 0.25) = 2.29%. Given that not all subjects will select the riskiest option in each case, these figures over-estimate the true probabilities of receiving high payments over $50.
Pre-test results. Pre-testing with 9 subjects yielded payoffs of $10.00 - $29.80, with session lengths ranging from 47 – 74 minutes. Median payout was $23.33, and median run-time was 62 minutes.
Total cost of the experiment. We anticipate average per subject earnings of between $20-25 (including a $10 show-up fee). We anticipate recruiting up to 500 student participants, bringing the expected total cost of subject payments to $10,000 - $12,500.
Additional efforts made to control total cost of the experiment. In designing our experimental procedures and payment levels, we took into consideration academic standards for normal payoff ranges for student and non-student populations, statistical power considerations, budgetary limitations, and the history of discussions between OMB and ERS regarding other research approved under the previous generic clearance (OMB control # 0536-0070).
High payment scales are commonly used for studies of risk preferences with student and non-student populations (see Table 4). We allow for the possibility of high payments consistent with academic norms in 9 out of 65 rounds (13.85% of rounds). This allows our experiment to be consistent with academic norms and improve our power to measure accurate risk preferences (see discussion in next section), while ensuring that average subject payments are consistent with OMB guidance on research payments for human subjects.
Table 4: Sample of Payment Scales Used for Studies Involving Risk Preference Elicitations
Paper |
Location of Sample |
Population Type |
Maximum Feasible Risky Payment |
Holt and Laury (2002) |
USA |
Student |
USD $346.50 |
Andersen et al (2008) |
Denmark |
Non-Student |
4500 DKK (USD $687) |
Bruhin et al (2010) |
Switzerland and China |
Student |
150 Euros (USD$169.50) |
Gaudecker et al (2011) |
Netherlands |
Non-Student |
87 Euros (USD $98.31) |
Dohmen et al (2011) |
Germany |
Non-Student |
300 Euros (USD $339) |
Bocqueho et al (2014) |
France |
Farmers |
120 Euros (USD $135.60) |
Comeig et al (2015) |
USA |
Student |
USD $125 |
We also considered the possibility of using an experimental currency or point system instead of delimiting payments directly in USD$. The object of using such an experimental currency would be to give the appearance of large value risks to subjects while still controlling the total cost of the experiment. Although experimental currencies are commonly used in other types of experiments (e.g. market experiments, public goods experiments, monetary theory experiments), neither Dr. Holt nor Dr. Rutstrom2 is aware of any study that has ever used an experimental currency for an experiment involving risk preferences. Holt and Laury (2002, 2005) document a large bias in risk preference estimates when student subjects do not expect to be paid for the decisions made in the experiment. von Gaudecker et al. (2011) show a similar hypothetical bias in risk preference estimates for a representative sample of the Dutch population. The informal consensus view in the academic community, according to Dr. Holt and Dr. Rutstrom, is that an experimental currency is likely to be subject to bias in a similar manner to the bias attached to hypothetical payments.
Because we have found no risk elicitation experiments that use experimental currencies, we are also unable to document an effect of using a variable-rate exchange rate for experimental currency for this type of experiment. In the next section, we document improvement in instrument power with increasing payoff scales. A variable-rate exchange rate could introduce a new potential source of error if subjects have idiosyncratic variation in their ability to keep track of actual payment values separately from displayed experimental currency values. This new type of error has the potential to attenuate the power benefits achieved with higher payment scales.
Because we could not establish precedent for using an experimental currency in a risk elicitation experiment, we chose instead to denominate risks in real US currency, but reduce the total number of high-stakes risks overall such that that probability of receiving large payoffs ($50 or more) was very small.
Outcomes of Interest, Calibration of Instruments, and Power Analyses
This experiment will generate multiple outcomes of interest. In this section, we define all outcomes of interest and how they will be generated from the different portions of the experiment, and review all steps involved in calculating the required sample size. For this experiment, sample size analyses consists of two steps. First, we show that how our intended calibration of instruments used in the experiment will increase their precision and improve our ability to measure specific outcomes of interest. Second, we calculate required sample size to detect treatment effects for one specific outcome of interest, insurance demand elasticity, given our chosen instrument calibrations.
Outcomes of Interest
This experiment will have multiple outcomes of interest:
Individual specific parameters for CPT utility function (four parameters)
Individual specific parameter for tendency to engage in MLA (one parameter)
Individual specific price and cross-price demand elasticities for insurance and cover crops (four parameters)
Regression coefficients for demographic characteristics’ effect on measured CPT and MLA parameters
Regression coefficients for demographic characteristics’ effect on measured demand elasticities
Regression coefficients for measured prospect theory and myopic loss aversion parameters’ effect on measured demand elasticities
Parameters for the prospect theory utility function and myopic loss aversion will be estimated using the data collected in rounds 1-20 of the experiment. Price and cross-price demand elasticities for insurance and cover crops will be estimated using the data collected in rounds 21-65 of the experiment. Demographic characteristics will be collected through the demographic questionnaire at the end of the experiment.
Calibration of Instrument to Measure Insurance Demand Elasticity
Econometric estimates of crop insurance demand elasticity range from -0.28 to -.4 for corn producers (Goodwin, 1993; Goodwin et al, 2004; Shaik et al., 2008) and -0.58 to -0.65 for wheat producers (Coble et al., 1996; Smith and Baquet, 1996). These estimates are based on a limited range of subsidy levels applied to US crop insurance programs in the 1990s. Our experiment will include a greater range of subsidy levels to better reflect contemporary levels of insurance subsidies, as well as unsubsidized prices consistent with commercially available insurance for other types of goods (automotive, home, etc).
We use the estimate from Goodwin (1993) for our power calculations because it is calculated based on a large sample of farmers, has a point estimate close to the midpoint of all reported figures, and has relatively large standard deviation for the point estimate. As such, these figures should give a conservative lower bound for our minimum sample size.
We use the power command in Stata/IC 14.1 to calculate the required sample size for a one-sample mean test (t-test) of the null hypothesis elasticity = 0 against the alternate hypothesis of elasticity = -0.32. We assume a population standard deviation of 0.1582, and 80% power for a two-tailed test of statistical significance at the 95% confidence level. The Stata command is:
power onemean 0 -0.32, sd(0.1582)
Under these assumptions, the minimum sample size required is 5. Because we require two measurements to create a single observation of demand elasticity, we require at least 10 observations per individual in order to have adequate power to measure demand elasticity under our set of assumptions. We are planning to have 15 observations per individual to increase precision of the estimate given the wider range of price variation allowed for in the experiment compared to real-world data.
Calibration of Instrument to Measure Prospect Theory Utility Function
Experimental subjects demonstrate greater levels of risk aversion as payment stakes increase (Holt and Laury 2002, 2005; Comeig et al. 2015). This can be attributed to two factors. First, subjects’ attitudes towards risk may be different at different payment scales. Second, subjects may be putting more cognitive effort towards making decisions at different payment scales. The former constitutes the effect to be measured from the experimental instrument. The latter constitutes noise which interferes with our ability to estimate risk preferences using the experimental instrument. Neither Dr. Holt nor Dr. Rutstrom are aware of any published papers that report the contribution of measurement error attributable to this cognitive effort component.
We construct a model of measurement error based on the experimental instrument used by Bruhin et al. (2010). Their instrument is similar to the instrument we plan to use in the proposed experiment. Figure 2 shows an example menu from the Bruhin et al. instrument. Option A is a risky decision. Option B is a decision with a certain payoff. Subjects indicate all rows for which they prefer B to A and vice versa. The measurement recorded for this menu is the specific point where subjects switch from B to A.

Figure 2: Example Decision Menu from Bruhin et al. (2010)
Error occurs in this measurement when subjects’ transition from B to A at a row that does not reflect their true preference. In the example in figure 1, a hypothetical subject has chosen to switch from B to A at row 8, indicating a certainty equivalent of between CHF3 13-14. If this decision was subject to error and the subject’s true preferences were to switch at row 9, then the true preferences would be a certainty equivalent of between CHF 12-13 and the measurement error would be between CHF 0-1.
For larger scale decisions, such as a 75% chance of earning CHF 50 and a 25% chance of earning CHF 0, the range of guaranteed payoffs in column B scales to match the new high and low payoffs while the number of rows stays fixed. This means that the difference in certain payoffs between rows is more than CHF 1, and therefore, that measurement error from selecting an incorrect row will also scale accordingly.
We decompose measurement error into two components4: an ambivalence effect and a scale5 effect. The ambivalence effect accounts for variation in cognitive attention applied at different payment scales. The scale effect accounts for differences in the magnitude of payments represented by each row. We specify the model as:
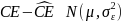
where
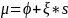 and
and
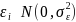 .
In our model,
.
In our model,
 is
the discrepancy between the subjects’ certainty equivalent and
a risk-neutral person’s certainty equivalent, s is the
scale of the lottery,
is
the discrepancy between the subjects’ certainty equivalent and
a risk-neutral person’s certainty equivalent, s is the
scale of the lottery,
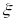 is the
proportional change in error size according to changes in scale, and
is the
proportional change in error size according to changes in scale, and
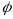 is a
measure of risk aversion. If
is a
measure of risk aversion. If
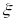 is
decreasing at higher payment scales, than the contribution of
ambivalence error to total error will shrink as payoff scale grows,
making the estimates more precise.
is
decreasing at higher payment scales, than the contribution of
ambivalence error to total error will shrink as payoff scale grows,
making the estimates more precise.
We statistically test this error structure model using a random coefficients model. To estimate this model, we use the following regression equations:
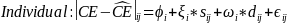
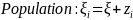
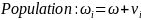
where i is an individual subject, j is a decision, and z, v and ϵ are random error terms. z and v capture the within-subject error, and ϵ is a white noise error. d is a dummy variable equal to 1 when scale exceeds 50. If ambivalence does not impact the precision of our instrument for different payoff scales, then the coefficient on the dummy term will not be statistically significantly different from zero.
We use publically available replication data provided by Bruhin et al to estimate our error structure model. This data set includes measurements of risk preferences for two samples of Swiss students and one sample of Chinese students (510 subjects total) using an experimental instrument similar to the instrument we propose to use in our experimental design. Converted from local currency to USD, the range of payments included in the instrument were USD $0 - $197.
The replication dataset is a panel of individual-level decisions. Individuals were asked to complete a series of either 28, 40, or 50 decisions. Some individuals did not complete their full sequence of decisions and were omitted from our analysis. Table 5 summarizes the data structure.
Table 5: Structure of Panel Data
|
Zurich 2003 |
China 2005 |
Zurich 2006 |
All |
Number of Subjects |
187 |
185 |
138 |
510 |
Number of Subjects with Complete Observations |
143 |
148 |
78 |
369
|
Observations per Subject |
50 |
28 |
40 |
|
Total Observations |
7,150 |
4,144 |
3,120 |
14,414 |
Regression
results are below. We estimate the error structure model with
mixed-effect maximum likelihood estimation using the mixed command in
Stata/IC version14.1. To account for heteroscedasticity, we use logs
of the dependent and independent variables.6
Estimated intercept ( and
regression coefficients for the scale of the lottery (ξ) and dummy
indicator (ω) are statistically significant at the 99% level
and have the expected signs.
and
regression coefficients for the scale of the lottery (ξ) and dummy
indicator (ω) are statistically significant at the 99% level
and have the expected signs.
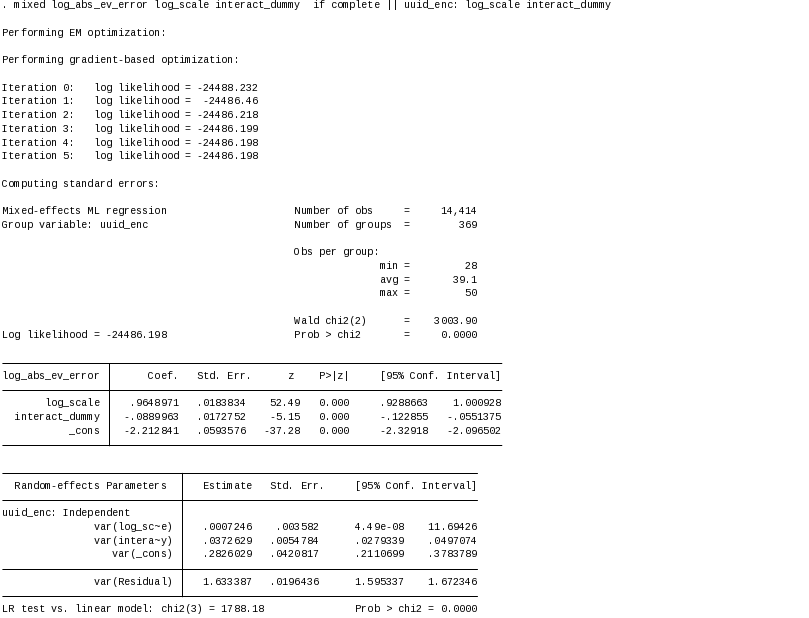
Results show that, on average, the population sampled is risk averse. The coefficient on the constant term is corresponds to a 0.11 CHF premium for certainty over a risk neutral person valuation. The coefficient on the scale term indicates that a 1% increase in the scale of payments translates into an almost 1% increase in measurement error – exactly what we would expect to see for measurement error induced by keeping the number of rows fixed across menus and applying linear payment scaling across rows. However, this contribution to measurement error is reduced by 8% for decisions involving payment scales of over 50 CHF.
Nationally representative studies of risk preferences (von Gaudecker et al, 2011; Dohmen et al, 2011; Choi et al, 2014), as well as studies using students (Bruhin et al, 2010) and farmers (Bocqueho et al, 2014), demonstrate substantial population heterogeneities in risk parameters. As we would expect, our results also show population heterogeneity for risk aversion. We also find population heterogeneity in response to high payment scale risks, but essentially no variation in response to measurement error from the scale variable. These findings are consistent with our assumptions about the source of measurement error for this type of risk preferences instrument.
Our results show that subjects display less noise in decisions involving large payoff differences (> 50 CHF) compared to the noise generated for decisions involving small payoff differences. Similar to the instrument used by Bruhin et al., our risk preference instrument will include a mixture of risk decisions over low payoff stakes and high payoff stakes. Increasing the share of risk decisions with high payoff stakes should improve statistical power but will also increase the likelihood of subjects’ receiving payouts of $50 or more. Therefore, we designed our risk preferences instrument to include a small number of high stakes decisions to improve estimate precision, and a larger number of decisions over smaller scale risks that are less informative but reduce the expected payoffs for student subjects.
Power Analysis for Choice of Sample Size
Our proposed experiment has four between-subjects treatments to vary the risk environment in which subjects make their insurance purchases. We calculate our minimum sample size required to achieve a minimum detectable effect (MDE) of 20% average differences in insurance demand elasticities across treatments.
We use the power command in Stata/IC 14.1 to calculate the required sample size for a two-sample means test (independent samples t-test) of a 20% MDE between treatments against the null hypothesis of no difference in average insurance demand elasticity between treatments. As before, we assume a population mean difference of -0.32, a standard deviation of population mean differences of 0.1582, and 80% power for a two-tailed test of statistical significance at the 95% confidence level. The Stata command is:
power twomeans -0.32, sd(0.1582) diff(-0.06)
Under these assumptions, we require at least 111 subjects per treatment group to have adequate power to detect differences in average insurance demand elasticities across treatments. This implies a minimum total sample size of 444 subjects for the full experiment. We plan to recruit no more than 500 subjects. We have selected our sample size at slightly higher than the minimum required sample size to accommodate (1) any subjects who respond to recruitment emails but are unable to participate because the session is over-subscribed, and (2) any subjects who decide to withdraw from the experiment before completing the full procedure.
References
Andersen, S., Harrison, G. W., Lau, M. I., & Rutström, E. E. (2008). Eliciting risk and time preferences. Econometrica, 76(3), 583–618.
Bocquého, G., Jacquet, F., & Reynaud, A. (2014). Expected utility or prospect theory maximisers? Assessing farmers’ risk behaviour from field-experiment data. European Review of Agricultural Economics, 41(1), 135–172.
Bruhin, A., Fehr-Duda, H., & Epper, T. (2010). Risk and rationality: Uncovering heterogeneity in probability distortion. Econometrica, 1375–1412.
Choi, S., Kariv, S., Müller, W., & Silverman, D. (2014). Who is (more) rational?. The American Economic Review, 104(6), 1518-1550.
Coble, K. H., Knight, T. O., Pope, R. D., & Williams, J. R. (1996). Modeling farm-level crop insurance demand with panel data. American Journal of Agricultural Economics, 78(2), 439-447.
Comeig, I., Holt, C. A., & Jaramillo-Gutiérrez, A. (2015). Dealing with risk: Gender, stakes, and probability effects (No. 0215). University of Valencia, ERI-CES.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G. G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Gaudecker, H.-M. von, Soest, A. van, & Wengström, E. (2011). Heterogeneity in Risky Choice Behavior in a Broad Population. The American Economic Review, 101(2), 664–694.
Goodwin, B. K. (1993). An empirical analysis of the demand for multiple peril crop insurance. American Journal of Agricultural Economics, 75(2), 425-434.
Goodwin, B. K., Vandeveer, M. L., & Deal, J. L. (2004). An empirical analysis of acreage effects of participation in the federal crop insurance program. American Journal of Agricultural Economics, 86(4), 1058-1077.
Holt, C. A., & Laury, S. K. (2002). Risk aversion and incentive effects. The American Economic Review, 92(5), 1644-1655.
Holt, C. A., & Laury, S. K. (2005). Risk aversion and incentive effects: New data without order effects. The American Economic Review, 95(3), 902-904.
Shaik, S., Coble, K. H., Knight, T. O., Baquet, A. E., & Patrick, G. F. (2008). Crop revenue and yield insurance demand: a subjective probability approach. Journal of Agricultural and Applied Economics, 40(3), 757-66.
Smith, V. H., & Baquet, A. E. (1996). The demand for multiple peril crop insurance: evidence from Montana wheat farms. American journal of agricultural economics, 78(1), 189-201.
1 Negative payments are subtracted from subjects’ show up fee. The minimum possible earnings from the experiment are $10 - $4.50 = $5.50.
2 Dr. Holt and Dr. Rutstrom are acknowledged experts on the subject of risk elicitation experiments. Their credentials are detailed in Part A of this application.
3 CHF is the abbreviation for Swiss Francs, the currency used in Switzerland.
4 As the academic literature has not yet considered this question, we relied on guidance from Dr. Holt and Dr. Rutstrom in establishing our modeling assumptions.
5 Scale of the lottery is measured as the absolute value of the difference between two possible payoffs in a binary risky decision.
6 We also tested for autocorrelation within our panel data. Although tests do indicate the presence of autocorrelation, coefficient estimates for a model that accounts for autocorrelation are essentially unchanged from our preferred specification. Results available upon request.
Supporting Statement: Attachment B Page
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Rosch, Stephanie - ERS |
| File Modified | 0000-00-00 |
| File Created | 2021-01-21 |
© 2025 OMB.report | Privacy Policy