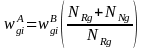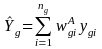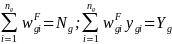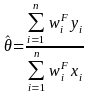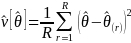Attachment G: Weighting and Estimation Procedures
FMLA Wave 4 Surveys_OMB Attachment G_Weighting and Estimation Procedures_3-17-17.docx
Family and Medical Leave Act, Wave 4 Surveys
Attachment G: Weighting and Estimation Procedures
OMB: 1290-0015
ATTACHMENT G
Attachment G: Weighting and Estimation Procedures
As introduced in Part B (see Sections B.2.1 and B.2.2), this attachment provides greater detail on the weighting and estimation procedures to be used for the Wave 4 FMLA Employee and Employer Surveys. Sections G.1 and G.2 discuss the weighting protocols for the Employee and Employer Surveys, respectively, and Section G.3 explains the variance estimation approach to be used for both surveys. Finally, Section G.4 discusses how to create employee-level estimates using data from the Employer Survey.
G.1. Employee Survey: Weighting Protocol
As discussed in Section B.1.1, the Employee Survey features a national, dual-frame cellular and landline random digit dial (RDD) probability sample design, through which any individual that has either a cellphone or a household landline can be reached. The landline and cellphone sampling frames overlap, as some individuals age 18 years and older have both a residential landline in their household and a cellphone (dual users). While earlier waves of the survey attempted to treat cellphones as a household device, and identify household members eligible for the survey, the efficiency of the rostering and handoff procedures on cellphones proved to be too low to be practical. Hence, in accordance with current survey industry practices, the Wave 4 FMLA Employee Survey will treat cellphones as an individual device (AAPOR 2010). The weighting procedures described in detail here (see also Part B, Section B.2.1) account for the overall probability of selection, integration of the two sampling frames, and appropriate nonresponse and post-stratification ratio adjustments.
As introduced in Part B, Section B.2.1, the reciprocals of the overall selection probabilities are referred to as “base weights.” These base weights will vary depending on the frame from which an individual is drawn, and some of the frame or survey variables. They are the product of four components:
The inverse of the selection probability of the sample telephone number (varies between the cell frame and the landline frame, and is higher for paid leave states);
An adjustment for the number of voice-use landline numbers in the household (not used for cell-only households) and the number of non-business adult-use cellphones in the household (not used for landline-only households);
An oversampling factor for prepaid flag status for cellphones (not used for landline-only households); and
In the case of persons employed at some point in the last 12 months, the inverse of the subsampling rate that is used (for leave-takers, leave-needers, or others).
The fourth component of the base weight consists of two multiplicative factors. In the landline frame, the first factor arises from the classification of all eligible employed adults1 in the household into the three “leave groups”: leave-takers, leave-needers, and employed-only.2 Among the groups present in a household (i.e., leave groups containing one or more persons), one group will be selected with a known probability, determined by the group subsampling probability used in the sample replicate from which the telephone number comes. The second factor that enters into the fourth component listed above arises from the random selection of one person from the sampled group. This factor equals one if the sampled group only contains one person. We may decide to put a cap on the maximum value allowed for the number of persons in the sampled group, to avoid extreme design weight values. In the cell frame, a parallel procedure will be used to build the fourth component of the base weight, with subsampling of individuals based on their leave group status.
Due to the overlap in the landline and cellular RDD frames, a frame integration weight (or “compositing factor” ) is needed to combine the two sample components. Landline-only and cellphone-only cases will be assigned a frame integration weight of one (=1). The frame integrated weights of dual users (i.e., persons who can be reached on both a landline and cellphone) will be adjusted for the overlap in the following way:
(1)
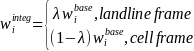
where
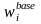 is the base weight. This frame integration compositing factor will
be chosen to minimize the design effect due to unequal weighting
(which has the effect of maximizing statistical power). The product
of the base weight and the frame integration compositing factor is
referred to as the “integration weight” and will be used
as the input weight for the nonresponse adjustment.
is the base weight. This frame integration compositing factor will
be chosen to minimize the design effect due to unequal weighting
(which has the effect of maximizing statistical power). The product
of the base weight and the frame integration compositing factor is
referred to as the “integration weight” and will be used
as the input weight for the nonresponse adjustment.
The screener nonresponse adjustment (see Part B, Section B.3.1) will need to be calculated at the individual level (for the cell frame) and at the household level (for the landline frame) for telephone numbers for which no screening interview is conducted. The adjustment cells will be based on region for both the cell and landline samples, and on auxiliary flags such as prepaid status for the cell sample. For the landline cases, the interview nonresponse adjustment will account for persons who have been listed on a household roster and selected for the sample, but an interview was not completed. The person-level interview nonresponse adjustment will be done within specified nonresponse adjustment weighting classes of persons, and these factors will be applied to the design weights adjusted for household nonresponse to compensate for unit nonresponse. The weighting classes will be defined by the age and gender of the sampled person. Interviewers will attempt to collect these variables on all adults on the survey roster. For item nonresponse on the weighting class variables (i.e., age and gender for household rosters on landline), missing data will be filled using model-based imputation methodology (van Buuren 2012).
The nonresponse-adjusted weight,
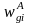 ,
for the i-th responding eligible person in weighting class g
will be computed as
,
for the i-th responding eligible person in weighting class g
will be computed as
|
(2) |
where
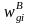 is the weight that includes the design weight and the
nonresponse adjustment, NRg
is the weighted sum of eligible responding persons in
weighting class g, and NNg
is the weighted sum of eligible non-responding persons in
weighting class g.
is the weight that includes the design weight and the
nonresponse adjustment, NRg
is the weighted sum of eligible responding persons in
weighting class g, and NNg
is the weighted sum of eligible non-responding persons in
weighting class g.
To help reduce possible residual nonresponse and non-coverage errors, the final estimation weights will also include a calibration adjustment to reflect the most recent population information available. First, the interview sample who respond to the survey screener will be calibrated to the general population characteristics. The control totals for this calibration step will come from the latest American Community Survey (ACS) and National Health Interview Survey (NHIS) microdata that are available at the time weighting is performed. The ACS data will be used to calibrate the demographic distributions for gender, age, education, race, Hispanic ethnicity, and region, while NHIS data will be used to calibrate the distribution across telephone service groups.3
Second, the sample who respond to the extended survey will be calibrated to the target population for the Employee Survey (adults age 18 and older residing in the U.S. who have been employed in the last 12 months). The control totals for the calibration of the second sample will come from the latest available March Current Population Survey, Annual Social and Economic Supplement (ACS-ASEC).4
The calibration variables will be constructed using the relevant demographic variables collected in the Employee Survey. The proposed initial groups are detailed below:
GENDER 1=Male, 2=Female
AGE 1=18 to 29, 2=30 to 39, 3=40 to 49, 4=50 to 59, 5=60 and above
EDUCATION 1=High school graduate/GED or less, 2=Some college or Associate degree, 3=Bachelor’s degree, 4=Master’s, Doctorate, or professional school degree (e.g., MD, DDS, JD)
RACE_ETHNICITY 1=White only non-Hispanic, 2=Black only non-Hispanic, 3=Asian only non-Hispanic, 4=Other race or mixed race non-Hispanic, 5=Hispanic
REGION 1=Northeast, 2=Midwest, 3=South, 4=West
PHONE SERVICE 1=Cellphone only, 2=Landline only, 3=Dual service
We will fill missing data on these weighting variables using model-based imputation methodology (van Buuren 2012). After the calibration groups are created, we will check the distribution of each of these dimensions in the survey dataset. If any of the cells defined above contains less than 5 percent of the unweighted sample, that cell will be considered for collapsing with the most appropriate cell in the given dimension. For example, if less than 5 percent of the respondents are Asian-only non-Hispanic, then this cell could be collapsed with the cell for other race or mixed race non-Hispanic. The purpose of collapsing these cells is to avoid excessively large weight values, which reduce the precision of survey estimates. This procedure also helps to ensure that the raking algorithm (discussed below) will converge and generate a solution.
Given that the sample will be calibrated to several variables, we will use the “raking ratio” algorithm to calculate the final weights (Kolenikov 2014). In raking ratio adjustments, weights are iteratively post-stratified one calibration variable at a time, so that the marginal distribution on a given dimension agrees exactly between the sample (e.g., the Employer Survey) and the population (e.g., the ACS). Since performing this adjustment on one variable (e.g., education) is likely to disturb the previously achieved agreement on another variable (e.g., age), the process is repeated iteratively with an expectation of convergence, namely that the weights will stabilize and reflect the population distribution of the underlying variables.
G.2. Employer Survey: Weighting Protocol
As discussed in Part B, Section B.1.2, the Employer Survey sample of worksites will be drawn from the Dun & Bradstreet Dun’s Market Identifiers (DMI) file. In order to make statistically valid estimates from the survey results, it will be necessary to weight the sample data. As explained in Part B, Section B.2.2, the weight to be applied to each responding worksite is a function of the overall probability of selection, and appropriate nonresponse and post-stratification ratio adjustments. The reciprocals of the overall selection probabilities, which will vary depending on the size of the establishment, are referred to as “base weights.” These weights will produce unbiased estimates if there is no nonresponse in the survey. Since some nonresponse is almost certain, adjustment factors will be calculated within specified nonresponse adjustment weighting classes of establishments, and these factors will be applied to the base weights to compensate for unit nonresponse. The weighting classes will be created with the goal to minimize the bias due to nonresponse. Item nonresponse will be addressed using appropriate imputation methodology. Regression-based imputation is usually appropriate for continuous variables, and hot-deck imputation is often used for categorical variables.
The nonresponse-adjusted weight,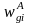 ,
for the i-th responding eligible establishment in weighting
class g will be computed following Equation 2 (see Section
G.1), where NRg
is the weighted sum of eligible responding establishments
in weighting class g, and NNg is
the weighted sum of eligible nonresponding establishments in
weighting class g. Sample establishments for whom eligibility
status is unknown will be excluded from the above nonresponse
adjustment.
,
for the i-th responding eligible establishment in weighting
class g will be computed following Equation 2 (see Section
G.1), where NRg
is the weighted sum of eligible responding establishments
in weighting class g, and NNg is
the weighted sum of eligible nonresponding establishments in
weighting class g. Sample establishments for whom eligibility
status is unknown will be excluded from the above nonresponse
adjustment.
To help reduce possible undercoverage errors in the DMI sampling frame and reduce possible nonresponse bias, the final estimation weights will also include a calibration adjustment to reflect the most recent population information available from the Quarterly Census of Employment and Wages (QCEW). The adjustments will be made using broad classes such as Census Region, paid vs. unpaid leave states, broad North American Industry Classification System [NAICS] category, and size of establishment. These groups will be defined based on analysis of the distributions of these variables in the QCEW data.
The adjustment cells will be constructed using the relevant variables in the Employer Survey dataset. The proposed initial groups are as follows:
Geography 1=Northeast non-paid leave states, 2=Midwest non-paid leave states, 3=South non-paid leave states, 4=West non-paid leave states; 5=Paid leave states
NAICS_SIZE A full cross-classification of the four NAICS groups and the four establishment size groups listed in Exhibit B.4 (see Part B).
We will fill missing data on these weighting variables using hot deck imputation methodology. After the post-strata are created but prior to raking, we will check the distribution of all dimensions in the Employer Survey dataset. As described in Section G.1, if any of the cells defined above contains less than 5 percent of the unweighted sample, that cell will be collapsed with the most appropriate cell in the given dimension.
The general approach for making the calibration
adjustment will use both the number of establishments and employment
as calibration variables using the expansion factors approach of
Kolenikov and Hammer (2015). Let
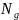 denote the total number of establishments in cell
denote the total number of establishments in cell
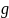 in
the population (i.e., the QCEW),
in
the population (i.e., the QCEW),
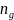 denote the total number of responding worksites in cell
denote the total number of responding worksites in cell
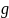 in
the sample (i.e., the Employer Survey), Yg
denote the aggregate number of employees in cell g as
given in the most recent QCEW data, and let
in
the sample (i.e., the Employer Survey), Yg
denote the aggregate number of employees in cell g as
given in the most recent QCEW data, and let
|
(3) |
denote the corresponding estimate from the sample,
where
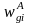 is the nonresponse-adjusted weight defined in Equation (2), and ygi
is the observed number of employees of establishment i in
cell g. The final weight
is the nonresponse-adjusted weight defined in Equation (2), and ygi
is the observed number of employees of establishment i in
cell g. The final weight
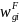 for establishment i in cell g will then be computed to
satisfy
for establishment i in cell g will then be computed to
satisfy
|
(4) |
The adjustment above has the effect of forcing the weighted estimate of the aggregate number of both establishments and employees in a cell to agree with the corresponding QCEW figures.
G.3: Variance Estimation
An important advantage of probability sampling methods is that they permit the calculation of the sampling errors (variances) associated with the survey estimates. Thus, with reasonably large samples, they provide an objective way of measuring the reliability of the survey results. The sampling errors may be calculated directly using analytical variance formulas, or by a replication procedure such as jackknife, balanced repeated replication, or the bootstrap.
Use of the direct variance estimators is relatively straightforward for simple linear estimates such as the Horvitz-Thompson expansion estimate of a population total. However, the analytical variance formulas can be complex for nonlinear statistics such as ratios (including means) or regression estimates. They will also be very complex for estimates based on the sample designs used for the Wave 4 FMLA surveys, which involve stratification, frame integration (for the Employee Survey), nonresponse adjustments, and calibration.
On the other hand, replication methods provide a relatively simple way of estimating variances with such complex sample designs. In addition, the impact of the nonresponse and post-stratification adjustments can be more easily reflected in the variance estimates obtained by replication methods.
Therefore, for both the Wave 4 Employee and Employer Surveys, we will calculate replicate weights to support variance estimation using the Rao-Wu complex survey rescaling bootstrap (Rao and Wu 1988; Rao, Wu, and Yue 1992; Kolenikov 2010). The bootstrap method is supported in all statistical software packages that have replicate variance estimation implemented, such as SAS, SUDAAN, Stata and R. As with any replication method, rescaling bootstrap involves (1) selecting a number of subsamples (replicates) from the full sample, (2) constructing weights using all the weighting steps discussed above, and (3) computing the statistic of interest for each replicate. The second step will be performed by survey statistics staff as a part of preparing the final Wave 4 FMLA survey data to be made publicly available. The third step will be performed by researchers as they analyze the survey data (documentation for the Wave 4 public use file will include sample code). Replicate variance estimation was used in the previous waves of FMLA surveys, and replicate weights were provided with each public dataset.
Specifically, let
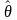 be any estimate from the survey. For example, if
be any estimate from the survey. For example, if
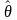 is an estimate of the proportion of employees who took family leave
in the past year, then
is an estimate of the proportion of employees who took family leave
in the past year, then
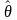 has the following form
has the following form
|
(5) |
where for each
establishment i,
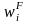 is
the final estimation weight as defined in Equation (4), yi
is the number of employees who
took family leave in the past year, and xi is the number of total
employees in the establishment. Further, let
is
the final estimation weight as defined in Equation (4), yi
is the number of employees who
took family leave in the past year, and xi is the number of total
employees in the establishment. Further, let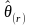 be
the corresponding estimate for a given replicate r. The estimate of
the sampling variance of
be
the corresponding estimate for a given replicate r. The estimate of
the sampling variance of
 can then be computed from the formula
can then be computed from the formula
|
(6) |
where the summation extends over all R
replicates. The necessary procedures are implemented in
statistical packages that support resampling complex variance
estimation, namely R, Stata, SAS, and SUDAAN. In the bootstrap
replicate variance estimation, samples with replacement are drawn
from each sampling stratum repeatedly
 times. This method is more robust than other resampling methods, in
that it allows variance estimation for a wider range of statistics
compared to the jackknife, and it does not involve arbitrary
assignments to pseudo-strata as required by group jackknife. For each
of the Wave 4 FMLA surveys, we propose to create 500 bootstrap
replicates; this is the number customarily used by Statistics Canada
in their bootstrap variance estimation procedures. For each of the
bootstrap replicates, all of the weighting steps (including
nonresponse adjustments, frame integration of the RDD frames in the
Employee Survey, and weight calibration) will be repeated, treating
the product of the base weight and the bootstrap frequency as the new
base weight. Doing so will ensure that all the improvements in the
estimates afforded by the final weights are properly reflected in the
standard errors around these estimates.
times. This method is more robust than other resampling methods, in
that it allows variance estimation for a wider range of statistics
compared to the jackknife, and it does not involve arbitrary
assignments to pseudo-strata as required by group jackknife. For each
of the Wave 4 FMLA surveys, we propose to create 500 bootstrap
replicates; this is the number customarily used by Statistics Canada
in their bootstrap variance estimation procedures. For each of the
bootstrap replicates, all of the weighting steps (including
nonresponse adjustments, frame integration of the RDD frames in the
Employee Survey, and weight calibration) will be repeated, treating
the product of the base weight and the bootstrap frequency as the new
base weight. Doing so will ensure that all the improvements in the
estimates afforded by the final weights are properly reflected in the
standard errors around these estimates.
G.4. Producing Employee Level Estimates from the Employer Survey
If the sample of worksites captured in the Wave 4 Employer Survey is representative of the population that provides employment, then the Employer Survey data on employees can be used to draw inferences on the population of employees (or at least on the part of this population employed at the target establishments). Thus, in addition to constructing the base and replicate weights that can be used to provide inference for the population of employers, for the Wave 4 Employer Survey we will use a method developed in Wave 3 to provide employee-level estimates from the Employer Survey.5 (See Part B, Section B.2.2 on the need to produce both worksite-level and employee-level estimates from the Employer Survey.)
For a worksite i, let ei be the number of employees, wi be the sampling weight of the worksite, zi be the worksite-level characteristic of interest (e.g., the number of unionized employees), and yi be the employee-level characteristic of interest (e.g., the percent of unionized employees). Also let be the population level of the characteristic of interest, in this case the percentage of unionized employees in the full universe U.
The population percentage of unionized employees is then
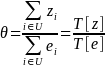 (7)
(7)
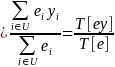 (8)
(8)
where
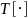 denotes the total of a given variable, and note that in this example,
zi = yi ei.
We can then estimate this population percentage as
denotes the total of a given variable, and note that in this example,
zi = yi ei.
We can then estimate this population percentage as
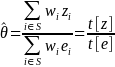 (9)
(9)
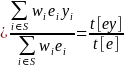 (10)
(10)
where
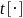 is
the estimate of the total of a given variable, and S
denotes the sample, in place of the whole universe U.6
is
the estimate of the total of a given variable, and S
denotes the sample, in place of the whole universe U.6
Note that in both Equation (9) and (10),
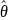 is
an estimator of a ratio (Lohr 2009; Korn and Graubard 1999). The
linearization estimator of the sampling variance of
is
an estimator of a ratio (Lohr 2009; Korn and Graubard 1999). The
linearization estimator of the sampling variance of
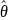 is
therefore given by
is
therefore given by
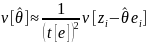 (11)
(11)
where
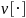 is
an appropriate estimator of the sampling variance of the quantity in
the brackets (e.g., the bootstrap variance estimator discussed in
Section G.3).7
Commands for computing the point estimates, variances and the design
effects for
is
an appropriate estimator of the sampling variance of the quantity in
the brackets (e.g., the bootstrap variance estimator discussed in
Section G.3).7
Commands for computing the point estimates, variances and the design
effects for
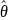 are available in complex survey software using ratios (e.g., PROC
SURVEYMEANS with RATIO statement in SAS, svy: ratio command in Stata,
svyratio() function in R and computed statistic in WesVar). Specific
instructions will be provided in the Wave 4 Methodology Report and
Public Use File User’s Guide.
are available in complex survey software using ratios (e.g., PROC
SURVEYMEANS with RATIO statement in SAS, svy: ratio command in Stata,
svyratio() function in R and computed statistic in WesVar). Specific
instructions will be provided in the Wave 4 Methodology Report and
Public Use File User’s Guide.
If the information of interest is available only at the individual level, on a per-employee basis (namely as a “y-type” variable in Equations 8 and 10), rather than at the worksite-level (as a “z-type” variable), then to follow the procedure descried above, it must first be scaled up to the worksite level. For instance, a worksite-level variable such as the total number of unionized employees in the worksite must first be created for the analysis.
Alternatively, when using replication variance
estimation methods, such as a bootstrap, a computational shortcut can
be taken with the individual-level y-type data. As is easily
seen from Equation (10), the estimate
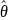 can be thought of as a weighted mean of yi,
with the weights given by
can be thought of as a weighted mean of yi,
with the weights given by
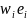 .
When the replicate values of
.
When the replicate values of
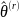 necessary for variance estimation are being computed, the main weight
necessary for variance estimation are being computed, the main weight
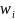 is
being replaced by the r-th replicate weight
is
being replaced by the r-th replicate weight
 .
Yet the expression (10) can still be interpreted as the weighted
mean, now with the weight given by the product
.
Yet the expression (10) can still be interpreted as the weighted
mean, now with the weight given by the product
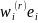 .
Hence, both the main sampling weight and the replicate weights can be
multiplied by the number of employees (ei),
and the statistic of interest and its standard error can be computed
as the weighted mean of yi with the doubly
expanded weight (
.
Hence, both the main sampling weight and the replicate weights can be
multiplied by the number of employees (ei),
and the statistic of interest and its standard error can be computed
as the weighted mean of yi with the doubly
expanded weight (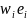 ),
rather than as the ratio
),
rather than as the ratio
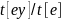 .
Again, this is easily implemented with complex survey-aware software
(svy: mean in Stata; PROC SURVEYMEANS in SAS; svymean in R; mean in
WesVar).
.
Again, this is easily implemented with complex survey-aware software
(svy: mean in Stata; PROC SURVEYMEANS in SAS; svymean in R; mean in
WesVar).
The drawback of this computational shortcut is
that it gives the wrong design effect. In terms of the equivalent
variance expression (11), the variance that needs to be computed is
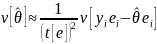 .
The shortcut procedure essentially factors out the employment
.
The shortcut procedure essentially factors out the employment
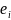 from the above procedure. However, when the variance under simple
random sampling—which is the denominator of the design
effect—is being computed, the weights are ignored as not
applicable, leading to an incorrect expression
from the above procedure. However, when the variance under simple
random sampling—which is the denominator of the design
effect—is being computed, the weights are ignored as not
applicable, leading to an incorrect expression
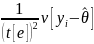 .
.
Another way to
explain the problem is to note that using the doubly expanded weight
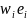 implies a sampling design in which one observation
on an employee is taken from each establishment. However, this is an
incorrect design specification; a data collection in which a
worksite-level variable (number of unionized employees) is being
observed should instead be interpreted as a one-stage cluster design,
in which all employees of the worksite i are observed, and their
characteristic of interest yi
(such as union membership) is measured. For this reason, the use of
the doubly expanded weights
implies a sampling design in which one observation
on an employee is taken from each establishment. However, this is an
incorrect design specification; a data collection in which a
worksite-level variable (number of unionized employees) is being
observed should instead be interpreted as a one-stage cluster design,
in which all employees of the worksite i are observed, and their
characteristic of interest yi
(such as union membership) is measured. For this reason, the use of
the doubly expanded weights
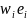 and their replicate analogues
and their replicate analogues
 should be treated with caution, and denominators of the design
effects may need to be calculated separately by the analyst
working with the data, rather than taken from the software defaults.
Examples of the problem, as well as specific instructions for correct
calculations, will be provided in the Wave 4 Methodology Report and
Public Use File User’s Guide.
should be treated with caution, and denominators of the design
effects may need to be calculated separately by the analyst
working with the data, rather than taken from the software defaults.
Examples of the problem, as well as specific instructions for correct
calculations, will be provided in the Wave 4 Methodology Report and
Public Use File User’s Guide.
References
AAPOR (American Association for Public Opinion Research). 2010. New Considerations for Survey Researchers When Planning and Conducting RDD Telephone Surveys in the U.S. with Respondents Reached via Cell Phone Numbers. Final Report of the AAPOR Cell Phone Task Force. Oakbrook Terrace, IL: American Association for Public Opinion Research.
Daley, Kelly, Courtney Kennedy, Marci Schalk, Julie Pacer, Allison Ackermann, Alyssa Pozniak, and Jacob Klerman. 2013. Family and Medical Leave in 2012: Methodology Report. Cambridge, MA: Abt Associates. http://www.dol.gov/asp/evaluation/fmla/FMLA-Methodology-Report-Appendices.pdf.
Kolenikov, Stanislav. 2010. “Resampling Variance Estimation for Complex Survey Data.” The Stata Journal 10 (2): 165-199.
Kolenikov, Stanislav. 2014. “Calibrating Survey Data Using Iterative Proportional Fitting (Raking)”. The Stata Journal 14 (1): 22–59.
Kolenikov, Stanislov, and Hammer, H. 2015. “Simultaneous Raking of Survey Weights at Multiple Levels.” Survey Methods: Insights from the Field, Special issue: ‘Weighting: Practical Issues and “How to” Approach. http://surveyinsights.org/?p=5099
Korn, E. L., and Graubard, B. I. 1999. Analysis of Health Surveys. New York: Wiley.
Lohr, S. 2009. Sampling: Design and Analysis. 2nd edition. Pacific Grove, CA: Duxbury Press.
Rao, J. N. K., and C. F. J. Wu. 1988. Resampling inference with complex survey data. Journal of the American Statistical Association 83 (401): 231-241.
Rao, J. N. K., C. F. J. Wu, and K. Yue. 1992. Some recent work on resampling methods for complex surveys. Survey Methodology 18 (2): 209-217.
van Buuren, Stef. 2012. Flexible Imputation of Missing Data. Chapman & Hall/CRC.
1 For the purpose of the Wave 4 Employee Survey, “employed adults” reflect persons 18 years or older who have worked for pay (private or public sector, other than self-employed) in the prior 12 months. On the cell frame, individuals who were not employed at any time in the last 12 months, and on the landline frame, households with no individuals employed at any time in the last 12 months, are not a part of the target population. The fourth component of their base weight will therefore be zero.
2 The survey will capture some individuals who have both taken leave in the last 12 months, and needed but not taken leave in those 12 months (termed “dual leave takers”). For subsampling purposes, they will be treated as leave-needers.
3 We will rely on the ACS instead of the CPS to calibrate the sample who respond to the survey screener because the ACS’s much larger sample size provides more accurate estimates. We must rely on the CPS to calibrate the screened sample because the ACS does not ask the employment questions that the Employee Survey screens on.
4 Specifically, we will use the CPS to estimate the total size of the target population, along with the same demographics distribution listed above (gender, age, etc.). We will compute the population benchmarks from the most up-to-date CPS monthly micro dataset that is publically available. We expect this to be the March 2017 dataset, with a reference period of January 2016 to December 2016; i.e., the 12 months prior to January 2017. Since the Employee Survey will ask about the previous 12 months and have a field period of November 2017 to April 2018, there will be some, but not exact, overlap with the field period of the CPS dataset. Consequently, there will be a slight misalignment between the “last 12 months” used to define the Employee Survey target population and the “last 12 months” for which employment is measured in the CPS dataset. Since the primary focus of the survey is not on short-term changes, we do not expect that the misalignment will be large enough to compromise the validity of the CPS data as control totals for this survey.
5 The method described here is based on Section 2.8 of the Methodology Report for the Wave 3 FMLA Surveys (Daley et al. 2013).
6 Depending on how the question is asked in the Wave 4 Employer Survey, the estimate of interest may have the form of (10) or (11).
7
Alternatively, the delta method for the total estimates
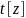 and
and
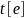 can be used to obtain
can be used to obtain
 (formula (2.4.7) in Korn and Graubard 1999).
(formula (2.4.7) in Korn and Graubard 1999).
Abt
Associates Supporting
Statement: Part A ▌pg.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 2021-01-22 |
© 2025 OMB.report | Privacy Policy