Sector Sampling Plan
Att. G - Mine Sampling Plans_March 17_Clean Copy.docx
Mining Industry and Workforce Survey (MIWS)
Sector Sampling Plan
OMB: 0920-1174
Mining Sector-Specific Sampling Plans
Separate sample designs are needed for each of the five commodity sectors. In this section, we present the stratification plan and sample sizes for the five sectors. The decision-making underlying each commodity’s stratification and sample size allocation tended to follow common guidelines across the five sectors. To avoid repetition, we begin by laying out the stratification and allocation guidelines first and then summarize the special attributes of each commodity’s design.
Mine-level and employee-level data analyses will be performed, requiring adequate sample sizes of mines and of employees. For mine-level analyses, NIOSH needs separate analysis capability for mines based upon mine type crossed with operation type crossed with employee size. Five mine types are of interest: (1) coal, (2) metal, (3) nonmetal, (4) stone and (5) sand and gravel. Operation type is defined as underground versus surface operations, where mines are classified as surface operations when they have no underground locations. Underground operations may have employees working in both underground and surface locations. Employee size categories are specific to each mine type by operation type combination, but across commodity types NIOSH needs separate analysis capabilities for small mines with 1 to 9 employees.
Because multiple employees are sampled from each responding mine, sample size requirements for mine-level analyses tend to be driven by the total number of mines needed for mine-level analyses. The sample size for employees is determined by the number of sampled mines responding and the average number of employees sampled per mine. The number of employees sampled per mine is variable, but the expected sample size is restricted to no more than 15 sampled employees per mine. In general, sample sizes have been set so that the expected MIWS sample of completed surveys would yield about as many completed surveys as that obtained by the 2008 NSMP, which sampled about 25 employees per mine instead of the maximum of 15 employees being used by MIWS but also had lower response rates than those projected for the MIWS.
The competing needs of mine-level analysis versus employee-level analysis require the use of a compromise design that supports the objectives of both types of analyses. For mine-level analyses, the best design is one that selects mines with equal probability, while for employee-level analyses the best design is one that selects mines with probability proportional to the number of employees. MIWS’s primary objective of obtaining employee statistics needed for risk analyses led to the decision to use a compromise design that stratifies mines by number of employees and then samples mines with equal probability within strata. Strata associated with large mines (in terms of employment) are given greater selection probabilities than small mines, which facilitates employee-level analyses by making the employee selection probabilities less variable across strata.
Mine size is an important domain for study at the mine level as well as at the employee level. Very small mines with less than ten employees tend to experience proportionately more serious injuries. Mines are also more likely to vary in their training procedures based upon employee size. Small mines are more likely to use trainers from outside the organization, while large mines tend to rely on in-house trainers. Hence, stratifying by number of employees in sampling mines serves an analytic purpose, as well as its role in facilitating the oversampling of large mines needed for employee-level analyses.
The probability of selection of an employee is the product of the probability of selection of his/her mine times the conditional probability of selection of the employee given that his/her mine is selected. The conditional probability of selection of an employee is equal within mines, as well as equal across mines with the same total employment. Mines with 10 or fewer employees will include all employees in the sample. Mines with 11 or more employees include either 10 or 15 employees in the sample depending on the stratum. This yields somewhat different selection probabilities based upon total employment.
From an analysis standpoint, it is also desirable to control for underground versus surface mines, when sampling mines and employees. Underground coal mines, in particular, have higher injury and fatality rates than surface mines (McWilliams et al., 2012). There is substantial diversity in the incidence of underground versus surface mines across commodity sectors. Nearly half of coal and metal mines are underground. Less than 10% of nonmetal and stone mines are underground and sand and gravel mines are surface only. Stratification by underground versus surface mine allows control over sample sizes needed for effective comparisons of underground mines to surface mines.
The
cum
 rule
is often suggested for use in forming strata for surveys of
businesses, which typically have a large number of small businesses
with very few employees and a small number of large businesses with
quite substantial payrolls (Cochran, 1977). Using this approach,
strata are established that have approximately equal sizes in terms
of the square root of the size measure. The cum
rule
is often suggested for use in forming strata for surveys of
businesses, which typically have a large number of small businesses
with very few employees and a small number of large businesses with
quite substantial payrolls (Cochran, 1977). Using this approach,
strata are established that have approximately equal sizes in terms
of the square root of the size measure. The cum
 rule
was used in determining the initial size-based strata for each mining
sector with an assumption of about 4-5 strata per commodity sector by
underground/surface operation type. Except for sand and gravel
mines, the large mines account for 25% or more of total employment.
Of necessity, stratum definitions must vary substantially across
mining sectors and operation types to account for the diversity of
mine operations across sectors.
rule
was used in determining the initial size-based strata for each mining
sector with an assumption of about 4-5 strata per commodity sector by
underground/surface operation type. Except for sand and gravel
mines, the large mines account for 25% or more of total employment.
Of necessity, stratum definitions must vary substantially across
mining sectors and operation types to account for the diversity of
mine operations across sectors.
The
next step was to determine the sample size needed for each commodity
survey and to allocate that sample to strata. To determine the
stratum sample sizes, we began by looking at precision of percentage
estimates under various sample sizes. Table 1 on page 21 presents the
half-length of confidence intervals around an estimated percentage
 under various sample size and design effects and assuming large
population sizes. For this table, the confidence interval was
approximated for design purposes as:
under various sample size and design effects and assuming large
population sizes. For this table, the confidence interval was
approximated for design purposes as:
 (1)
(1)
Here
z1-
is value of the critical point x at which the normal
cumulative distribution function equals 1-
and
 is
the estimated variance of
is
the estimated variance of .
The half-length HL is:
.
The half-length HL is:
 . (2)
. (2)
That
is,
 can be expected to fall within the range [P-HL, P+HL]
with 95% confidence for the indicted sample sizes.
can be expected to fall within the range [P-HL, P+HL]
with 95% confidence for the indicted sample sizes.
To
determine these half-lengths of confidence intervals, we need to
estimate the variance of the estimated percentage .
Ignoring finite population correction factors, Table 1 models the
estimated variance for an estimated percentage
.
Ignoring finite population correction factors, Table 1 models the
estimated variance for an estimated percentage
 as:
as:
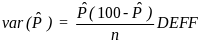 (3)
(3)
Where
n is the sample size,
 the
estimated percentage, and DEFF is the design effect.
the
estimated percentage, and DEFF is the design effect.
The
standard error of
 is the
square root of its estimated variance, and its 95% HL is roughly
twice its standard error. Observe from equation (3), that the
estimated variance (and thus the standard error and 95% HL) is
highest when
is the
square root of its estimated variance, and its 95% HL is roughly
twice its standard error. Observe from equation (3), that the
estimated variance (and thus the standard error and 95% HL) is
highest when
 =
50%.
=
50%.
The design effect for a survey estimate is defined to be the ratio of the statistic under the actual design divided by the variance that would have been achieved from a simple random sample of the same size. The design effect represents the cumulative effect of design components such as stratification, unequal weighting, and clustering and varies with each design. We expect design effects will be about 1.00 for mine-level and somewhat larger for employee-level estimates within strata. Cross cutting estimates are likely to have larger design effects particularly for employee-level estimates. The design effect differs from 1.00 for the cross cutting estimates due to the variation in sampling rates used across strata. Fortunately, these cross cutting estimates often have large sampler sizes due to combining sample across strata.
We
began setting sample sizes with the guideline that we wanted the
precision for stratum estimates to be that shown for sample sizes of
100 in Table 1. Some mine strata have very small population sizes and
some mining sectors are small overall. In such situations, the
variance as given in equation (3) is reduced by the factor ,
where n is the sample size and N is the population
size. Rather than create versions of Table 1 for all possible
population sizes, we developed what we refer to as
finite-population-corrected (fpc) sample sizes. An actual sample size
of n for a population of size N is equivalent to the
precision achieved with a sample size of
,
where n is the sample size and N is the population
size. Rather than create versions of Table 1 for all possible
population sizes, we developed what we refer to as
finite-population-corrected (fpc) sample sizes. An actual sample size
of n for a population of size N is equivalent to the
precision achieved with a sample size of
 from a population so large that fpc effects are ignorable. We set
initial sample sizes for each stratum so that the
finite-population-corrected sample size was about 100 and then
inflated these sample sizes to account for the projected 60% response
rate. These initial sample sizes were then adjusted to prevent
excessive variations in the sampling rates across strata for mines
and for employees.
from a population so large that fpc effects are ignorable. We set
initial sample sizes for each stratum so that the
finite-population-corrected sample size was about 100 and then
inflated these sample sizes to account for the projected 60% response
rate. These initial sample sizes were then adjusted to prevent
excessive variations in the sampling rates across strata for mines
and for employees.
Besides the number of mines selected, the employee sample size is affected by the eligibility and response rates for mines and the average number employees sampled per mine. The average number of employees sampled per mine is 15 employees except for the smaller strata, especially those that have total employee counts of 9 or fewer employees.
We assumed that 40% of all eligible mines would respond, providing both mine-level and employee-level data. This response rate is slightly larger than that achieved by the 2008 NSMP. The MIWS has been substantially redesigned to make achieving this response rate feasible. The mine-level questionnaire was simplified and substantially reduced in size. The maximum number of employees mines report for was reduced from about 25 to 15 and the number and complexity of the data requested was also reduced. NSMP required that each sampled mines select the systematic sample of employees using custom-generated Start-With and Take-Every Numbers. The MIWS will provide a customized selection table that each mine consults to get the sequential numbers associated with their 10 or 15 sampled employees. Strata containing some mines with fewer than 15 workers, will have no more than 10 sampled workers per sampled mine, the remaining strata will 15 sampled workers per sampled mine.
For sample design purposes, we used 2012 and 2013 MSHA Form 7000-2 data for Quarter 2 to estimate eligibility rates. The 2012 Quarter 2 data was used to create a mock frame by eliminating mines with zero employees. Then the 2013 Quarter 2 data was used for the remaining mines to estimate the fraction that would still be in operation one year later. These data were used to estimate separate eligibility rates for each stratum defined by commodity type by operation type by employee size.
In
designing the commodity samples, we sought to minimize the design
effects for employee-level analyses and as far as possible for
mine-level analyses as well. In particular, we sought to achieve
design effects of 1.0 for within-stratum mine-level estimates and
design effects of 2.0 or less for cross-cutting estimates.
Employee-level analyses tend to have larger design effects due to
unequal selection probabilities for employees due to the fixed sample
size of no more than ten employees sampled per mine. Following
standard practice, we modeled the design effect DEFF as the
product of the design effect associated with unequal weighting Dw
and the design effect for clustering Dc,
that is
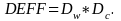 The 2012 and 2013 MSHA Quarter 2 data were again used to project the
values expected for the mine-level and employee-level design effects.
For comparison with our estimated design effects, note that a simple
random sample has both design effect components equal to one so
DEFF=1.
The 2012 and 2013 MSHA Quarter 2 data were again used to project the
values expected for the mine-level and employee-level design effects.
For comparison with our estimated design effects, note that a simple
random sample has both design effect components equal to one so
DEFF=1.
Both mine-level and employee-level estimates could potentially be subject to an unequal weighting effect greater than one, particularly for cross-cutting estimates that combine data from multiple strata. The design effect for unequal weighting can be estimated as:
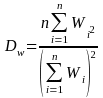 . (4)
. (4)
Here n is the total sample size and Wi is the weight for the ith observation. When the weights (the inverse of the selection probabilities) are equal for all selections, Dw = 1. For mines, Dw = 1.0 within all strata but is greater than 1.0 across strata. For employees Dw tends to be greater than 1.0, particularly for the two largest strata. These strata tend to have all mines selected with certainty, so the only way to reduce Dw would be to increase the number of employees sampled per mine from 10 to 20 or more. Adjusting the sample size for the very large mines would even out the employee-level weights within these strata and across strata. However, the increase in employee sample size increases the burden for the mine respondent and may result in much lower response rates for larger strata. It would also increase the design effect for clustering, which would negate some of the gains made by reducing the design effect for unequal weighting. As a consequence, the study team concluded that the number of employees sampled per mine should not be increased.
The design effect associated with clustering measures the loss of precision of a clustered sample as compared with a simple random sample. Clustered samples tend to have less precision than simple random samples of the same size, because units within the same cluster usually are more homogeneous than units from different clusters. The design effect for clustering can be estimated as:
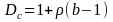 (5)
(5)
where ρ is the intracluster correlation coefficient and b is the cluster size. Because stratified sequential sampling will be used to select mines, the mines will not be clustered (b=1) and mine-level estimates will not be subject to a clustering effect (Dc=1). However, multiple employees will be selected from each mine, so employee-level estimates will be subject to a design effect due to clustering. For the purpose of modeling the clustering design effect, we assumed variable values for ρ based upon the size of the mine. Employees within very small mines with 1 to 9 employees were expected to be more homogeneous so a value of ρ = 5% was assumed. Small and medium size mines were assumed to be less homogeneous so a value of ρ = 3% was assumed. Large mines with more than 100 employees were expected to be quite diverse so a value of ρ =1% was assumed.
The remainder of this section presents the stratification and sample size allocation plan for each cycle of the MIWS and their associated mining commodities. These plans were developed using MSHA Form 7000-2 data for the second quarter of 2012 and 2013. The number of actual employees was used to develop these designs rather than the number of full time equivalent (FTE) employees, because the mine operator will be sampling based upon counts of actual employees not FTEs. Mines were classified as surface mines only when the mine had no employees working in underground locations.
Table 1: The Half Length of 95% Confidence Intervals in Percentage Points for Various Percentages Being Estimated for Domains of Various Sizes with Various Design Effects
Design Effect (DEFF) |
Percent (%) |
Domain Sample Size (Completed Interviews) |
||||||||
50 |
75 |
100 |
150 |
200 |
250 |
350 |
400 |
500 |
||
|
|
|
|
|
|
|
|
|
|
|
1.00 |
10 |
8 |
7 |
6 |
5 |
4 |
4 |
3 |
3 |
3 |
|
20 |
11 |
9 |
8 |
6 |
6 |
5 |
4 |
4 |
4 |
|
25 |
12 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
4 |
|
30 |
13 |
10 |
9 |
7 |
6 |
6 |
5 |
4 |
4 |
|
40 |
14 |
11 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
|
50 |
14 |
11 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
|
|
|
|
|
|
|
|
|
|
|
1.25 |
10 |
9 |
8 |
7 |
5 |
5 |
4 |
4 |
3 |
3 |
|
20 |
12 |
10 |
9 |
7 |
6 |
6 |
5 |
4 |
4 |
|
25 |
13 |
11 |
9 |
8 |
7 |
6 |
5 |
5 |
4 |
|
30 |
14 |
12 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
|
40 |
15 |
12 |
11 |
9 |
8 |
7 |
6 |
5 |
5 |
|
50 |
15 |
13 |
11 |
9 |
8 |
7 |
6 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
1.50 |
10 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
4 |
3 |
|
20 |
14 |
11 |
10 |
8 |
7 |
6 |
5 |
5 |
4 |
|
25 |
15 |
12 |
10 |
8 |
7 |
7 |
6 |
5 |
5 |
|
30 |
16 |
13 |
11 |
9 |
8 |
7 |
6 |
6 |
5 |
|
40 |
17 |
14 |
12 |
10 |
8 |
7 |
6 |
6 |
5 |
|
50 |
17 |
14 |
12 |
10 |
8 |
8 |
6 |
6 |
5 |
|
|
|
|
|
|
|
|
|
|
|
2.00 |
10 |
12 |
10 |
8 |
7 |
6 |
5 |
4 |
4 |
4 |
|
20 |
16 |
13 |
11 |
9 |
8 |
7 |
6 |
6 |
5 |
|
25 |
17 |
14 |
12 |
10 |
8 |
8 |
6 |
6 |
5 |
|
30 |
18 |
15 |
13 |
10 |
9 |
8 |
7 |
6 |
6 |
|
40 |
19 |
16 |
14 |
11 |
10 |
9 |
7 |
7 |
6 |
|
50 |
20 |
16 |
14 |
11 |
10 |
9 |
7 |
7 |
6 |
|
|
|
|
|
|
|
|
|
|
|
3.00 |
10 |
12 |
10 |
8 |
7 |
6 |
5 |
4 |
4 |
4 |
|
20 |
16 |
13 |
11 |
9 |
8 |
7 |
6 |
6 |
5 |
|
25 |
17 |
14 |
12 |
10 |
8 |
8 |
6 |
6 |
5 |
|
30 |
18 |
15 |
13 |
10 |
9 |
8 |
7 |
6 |
6 |
|
40 |
19 |
16 |
14 |
11 |
10 |
9 |
7 |
7 |
6 |
|
50 |
20 |
16 |
14 |
11 |
10 |
9 |
7 |
7 |
6 |
Table 2 presents the proposed stratification scheme and sample size allocation for stone mines and for sand and gravel mines and the projected standard errors for estimated proportions equal to 0.5 (the projected standard errors for other proportions will be lower).
Only 114 of the total 4,207 stone mines were underground mines (see Table 2). Because of the small number of underground stone mines, all underground mines were included in the sample. The 114 underground stone mines are expected to yield 46 responding eligible mines, who report for 492 employees.
A total of 55% of all surface stone mines had 1-9 employees, leading to the decision to partition this category into three strata with employee sizes of 1-3, 4-6, and 7-9. These three small strata contain 16% of total employees. The remaining surface stone mines tended to be small in comparison to those of other mining commodities leading to additional strata for mines with 10-19, 20-49 and 50 or more employees. The sample for stone mines was allocated to control for the size distribution of stone surface mines but these strata may need to be collapsed to ensure sufficient estimation capability. A total of 371 surface mines are to be sampled to yield 174 responding eligible mines, reporting for 1,638 employees. This sample size reduction reflects the differential effect of eligibility across strata (rates range from 80 to 100 percent) and the 40% response rate assumed for all strata.
All of the 5,819 sand and gravel mines are surface mines. Unlike the other mining commodity sectors, sand and gravel mines tend to be dominated by small mines. Small operations with 1-9 employees accounted for 86% of sand and gravel mines and 54% of total employment. There were only 19 moderately large operations with 50 or more employees and they accounted for only 5% of total sand and gravel employees. Sand and gravel mines were partitioned into strata using the same six strata used for stone surface mines: 1-3, 4-6, 7-9, 10-19, 20-49, and 50 or more employees. Again this allocation was used to control the sample distribution by employee size and some collapsing of strata may be needed in analysis. A total of 590 sand and gravel mines are to be sampled and expected to yield 216 eligible responding mines who report for 1,337 employees.
Table 2: Sample Allocation for Stone and Sand & Gravel Mines
Stratum |
N of Mines |
Percent of Mines |
Total Number of Employees |
Percent of Total Employees |
Sample Mines |
Eligibility Rate |
Response Rate |
Responding Eligible Mines |
Average Employees Sampled Per Mine |
Total Sample Employees |
Stone Underground |
||||||||||
1-9 |
13 |
11% |
68 |
1.5% |
13 |
100% |
40% |
5 |
8 |
42 |
10-19 |
23 |
20% |
340 |
7.3% |
23 |
100% |
40% |
9 |
9 |
83 |
20-49 |
50 |
44% |
1,603 |
34.5% |
50 |
100% |
40% |
20 |
10 |
200 |
50+ |
28 |
25% |
2,633 |
57% |
28 |
100% |
40% |
11 |
15 |
168 |
TOTAL: |
114 |
100% |
4,644 |
100.0% |
114 |
|
|
46 |
|
492 |
Stone Surface |
||||||||||
1-3 |
888 |
22% |
2,012 |
3.2% |
60 |
80% |
40% |
19 |
3 |
58 |
4-6 |
803 |
20% |
3,887 |
6.2% |
60 |
91% |
40% |
22 |
5 |
109 |
7-9 |
521 |
13% |
4,096 |
6.6% |
60 |
95% |
40% |
23 |
8 |
182 |
10-19 |
987 |
25% |
13,445 |
21.6% |
100 |
99% |
40% |
40 |
10 |
395 |
20-49 |
533 |
13% |
15,555 |
25.0% |
75 |
99% |
40% |
30 |
10 |
298 |
50+ |
226 |
6% |
23,292 |
37% |
100 |
100% |
40% |
40 |
15 |
597 |
TOTAL: |
4,093 |
100% |
62,287 |
100.0% |
371 |
|
|
174 |
|
1,638 |
Sand and Gravel |
||||||||||
1-3 |
2,725 |
47% |
5,857 |
17.1% |
203 |
85% |
85% |
69 |
2 |
137 |
4-6 |
1,599 |
28% |
7,663 |
22.3% |
120 |
90% |
90% |
43 |
5 |
217 |
7-9 |
632 |
11% |
4,938 |
14.4% |
48 |
93% |
93% |
18 |
7 |
125 |
10-19 |
654 |
10% |
8,692 |
25.3% |
95 |
97% |
97% |
37 |
9 |
331 |
20-49 |
190 |
3% |
5,375 |
15.7% |
105 |
98% |
98% |
41 |
10 |
413 |
50+ |
19 |
0% |
1,805 |
5% |
19 |
100% |
100% |
8 |
15 |
114 |
TOTAL: |
5,819 |
100% |
34,330 |
100.0% |
590 |
|
|
216 |
|
1,337 |
Table 2: Sample Allocation for Stone and Sand & Gravel Mines (Continued)
Stratum |
Nonresponse Adjusted Mine Weight |
Average Employee Weight |
Mine DEFF |
Employee DW |
Employee ρ |
Employee DC |
Employee DEFF |
Standard Error for an Estimated Mine Proportion of .5 |
Standard Error for an Estimated Employee Proportion of . 5 |
Stone Underground |
|
|
|||||||
1-9 |
1.7 |
2 |
1.0 |
1.0 |
5% |
1.35 |
1.4 |
0.219 |
0.090 |
10-19 |
1.7 |
3 |
1.0 |
1.2 |
3% |
1.24 |
1.5 |
0.165 |
0.067 |
20-49 |
1.7 |
5 |
1.0 |
1.1 |
3% |
1.27 |
1.4 |
0.112 |
0.042 |
50+ |
1.7 |
33 |
1.0 |
2.1 |
1% |
1.14 |
2.4 |
0.149 |
0.060 |
TOTAL: |
|
|
|
|
|
|
|
0.074 |
0.037 |
Stone Surface |
|
|
|||||||
1-3 |
38.3 |
38 |
1.0 |
1.0 |
5% |
1.10 |
1.1 |
0.114 |
0.069 |
4-6 |
37.4 |
38 |
1.0 |
1.0 |
5% |
1.20 |
1.2 |
0.107 |
0.052 |
7-9 |
23.1 |
25 |
1.0 |
1.0 |
5% |
1.25 |
1.4 |
0.105 |
0.041 |
10-19 |
16.4 |
24 |
1.0 |
1.1 |
3% |
1.27 |
1.4 |
0.079 |
0.030 |
20-49 |
16.7 |
53 |
1.0 |
1.1 |
3% |
1.42 |
1.6 |
0.092 |
0.036 |
50+ |
3.8 |
42 |
1.0 |
1.2 |
1% |
1.14 |
1.4 |
0.079 |
0.024 |
TOTAL: |
|
|
|
|
|
|
|
0.042 |
0.017 |
Sand and Gravel |
|
|
|||||||
1-3 |
37 |
37 |
1.0 |
1.0 |
5% |
1.05 |
1.1 |
0.060 |
0.044 |
4-6 |
37 |
37 |
1.0 |
1.0 |
5% |
1.20 |
1.2 |
0.076 |
0.037 |
7-9 |
36 |
36 |
1.0 |
1.0 |
5% |
1.30 |
1.3 |
0.118 |
0.051 |
10-19 |
17 |
24 |
1.0 |
1.2 |
3% |
1.24 |
1.5 |
0.082 |
0.034 |
20-49 |
4 |
15 |
1.0 |
1.2 |
1% |
1.09 |
1.3 |
0.078 |
0.028 |
50+ |
2 |
11 |
1.0 |
1.1 |
1% |
1.14 |
1.3 |
0.181 |
0.052 |
TOTAL: |
|
|
|
|
|
|
|
0.038 |
0.017 |
Table 3 presents the proposed stratification scheme and sample size allocation for metal and nonmetal mines and the projected standard errors for estimated proportions equal to 0.5 (the projected standard errors for other proportions will be lower).
As of the second quarter of 2016, there were 270 metal mines, of which more than two-thirds were surface mines (see Table 3). Small operations with 1-9 employees accounted for 41% of surface metal mines and 40% of underground mines but accounted for only 0.9% and 1.4% of the associated employment. Very large operations with more than 300 employees accounted for18% of surface mines and 14% of underground mines but employed 79% of total surface workers and 62% of underground workers. Initially, sample allocations were developed for each stratum accounting for the small populations of metal mines in each stratum. But these derived sample sizes were so close to the total population sizes that a decision was made to take all metal mines with certainty from every stratum. The 192 surface metal mines are expected to yield 66 eligible responding mines reporting for themselves and for 655 employees. The 78 underground metal mines are expected to yield 26 responding eligible metal mines reporting for themselves and for 273 employees.
Only 42 of the 853 nonmetal mines were underground mines. Because of the small number of underground nonmetal mines, all underground mines were included in the sample. The 42 underground nonmetal mines are expected to yield 17 responding eligible mines, who report for 173 employees.
Small surface operations with 1-9 employees accounted for 56% of surface nonmetal mines but only 9.6% of surface employment. Very large surface operations with more than 100 employees accounted for 4% of surface mines but employed 34% of surface workers. The sample for surface mines was allocated under the assumption that separate estimation capability was needed for mines with 1-9 employees, 10-49 employees, 50-99 employees, 100-299 employees, and 300 and more employees. A total of 385 surface mines are expected to need to be sampled to yield 143 responding eligible mines. These mines are expected to report for 1,379 surface nonmetal mine employees.
Table 3: Sample Allocation for Metal and Nonmetal Mines
Stratum |
N of Mines |
Percent of Mines |
Total Number of Employees |
Percent of Total Employees |
Sample Mines |
Eligibility Rate |
Response Rate |
Responding Eligible Mines |
Average Employees Sampled Per Mine |
Total Sample Employees |
Metal Surface |
||||||||||
1-9 |
78 |
41% |
274 |
1% |
78 |
73% |
40% |
23 |
5 |
114 |
10-99 |
57 |
30% |
1,926 |
7% |
57 |
91% |
40% |
21 |
10 |
207 |
100-299 |
22 |
12% |
4,072 |
14% |
22 |
94% |
40% |
8 |
15 |
124 |
300-599 |
20 |
10% |
8,656 |
30% |
20 |
100% |
40% |
8 |
15 |
120 |
600+ |
15 |
8% |
14,298 |
49% |
15 |
100% |
40% |
6 |
15 |
90 |
TOTAL: |
192 |
100% |
29,226 |
100% |
192 |
87% |
40% |
66 |
|
655 |
Metal Underground |
||||||||||
1-9 |
31 |
40% |
119 |
1% |
31 |
67% |
40% |
8 |
5 |
42 |
10-99 |
21 |
27% |
782 |
10% |
21 |
89% |
40% |
7 |
8 |
75 |
100-299 |
15 |
19% |
2,172 |
27% |
15 |
100% |
40% |
6 |
15 |
90 |
300-499 |
7 |
9% |
2,464 |
31% |
7 |
100% |
40% |
3 |
15 |
42 |
500+ |
4 |
5% |
2,507 |
31% |
4 |
100% |
40% |
2 |
15 |
24 |
TOTAL: |
78 |
100% |
8,044 |
100% |
78 |
|
40% |
26 |
|
273 |
Nonmetal Surface |
||||||||||
1-9 |
455 |
56% |
1,761 |
10% |
150 |
85% |
40% |
51 |
4 |
255 |
10-49 |
256 |
32% |
5,791 |
32% |
135 |
97% |
40% |
52 |
10 |
524 |
50-99 |
70 |
9% |
4,587 |
25% |
70 |
100% |
40% |
28 |
15 |
420 |
100-299 |
25 |
3% |
3,980 |
22% |
25 |
100% |
40% |
10 |
15 |
150 |
300+ |
5 |
1% |
2,131 |
12% |
5 |
100% |
40% |
2 |
15 |
30 |
TOTAL: |
811 |
100% |
18,250 |
100% |
385 |
|
40% |
143 |
|
1,379 |
Nonmetal Underground |
||||||||||
1-9 |
12 |
29% |
47 |
1% |
12 |
89% |
40% |
4 |
5 |
21 |
10-99 |
14 |
33% |
731 |
12% |
14 |
100% |
40% |
6 |
10 |
56 |
100-299 |
9 |
21% |
1,760 |
30% |
9 |
100% |
40% |
4 |
15 |
54 |
300+ |
7 |
17% |
3,380 |
57% |
7 |
100% |
40% |
3 |
15 |
42 |
TOTAL: |
42 |
100% |
5,918 |
100% |
42 |
|
40% |
17 |
|
173 |
Table 3: Sample Allocation for Metal and Nonmetal Mines (Continued)
Stratum |
Nonresponse Adjusted Mine Weight |
Average Employee Weight |
Mine DEFF |
Employee DW |
Employee ρ |
Employee DC |
Employee DEFF |
Standard Error for an Estimated Mine Proportion of .5 |
Standard Error for an Estimated Employee Proportion of . 5 |
Metal Surface |
|
|
|||||||
1-9 |
1.7 |
3 |
1.0 |
1.4 |
5% |
1.19 |
1.7 |
.105 |
.060 |
10-99 |
1.7 |
7 |
1.0 |
1.5 |
3% |
1.26 |
1.9 |
.110 |
.048 |
100-299 |
1.7 |
45 |
1.0 |
1.2 |
1% |
1.09 |
1.3 |
.174 |
.053 |
300-599 |
1.7 |
95 |
1.0 |
1.1 |
1% |
1.09 |
1.2 |
.177 |
.051 |
600+ |
1.7 |
211 |
1.0 |
1.3 |
1% |
1.09 |
1.5 |
.204 |
.064 |
TOTAL: |
|
|
|
|
|
|
|
0.62 |
.036 |
Metal Underground |
|
|
|||||||
1-9 |
1.7 |
2 |
1.0 |
1.4 |
5% |
1.19 |
1.7 |
.173 |
.100 |
10-99 |
1.7 |
14 |
1.0 |
1.1 |
3% |
1.22 |
1.4 |
.183 |
.068 |
100-299 |
1.7 |
35 |
1.0 |
1.1 |
1% |
1.09 |
1.2 |
.204 |
.059 |
300-499 |
1.7 |
70 |
1.0 |
0.9 |
1% |
1.09 |
1.0 |
.299 |
.078 |
500+ |
1.7 |
141 |
1.0 |
1.0 |
1% |
1.09 |
1.1 |
.395 |
.109 |
TOTAL: |
|
|
|
|
|
|
|
.098 |
.046 |
Nonmetal Surface |
|
|
|||||||
1-9 |
4.8 |
6 |
1.0 |
1.6 |
5% |
1.16 |
1.8 |
.070 |
.043 |
10-49 |
3.5 |
10 |
1.0 |
1.2 |
3% |
1.26 |
1.5 |
.069 |
.027 |
50-99 |
1.7 |
12 |
1.0 |
1.1 |
3% |
1.27 |
1.4 |
.094 |
.030 |
100-299 |
1.7 |
32 |
1.0 |
1.1 |
1% |
1.09 |
1.2 |
.158 |
.046 |
300+ |
1.7 |
96 |
1.0 |
1.2 |
1% |
1.09 |
1.3 |
.354 |
.107 |
TOTAL: |
|
|
|
|
|
|
|
.045 |
.020 |
Nonmetal Underground |
|
|
|||||||
1-9 |
1.7 |
2 |
1.0 |
1.0 |
5% |
1.19 |
1.2 |
.242 |
.118 |
10-99 |
1.7 |
9 |
1.0 |
1.2 |
3% |
1.26 |
1.5 |
.211 |
.082 |
100-299 |
1.7 |
30 |
1.0 |
1.1 |
1% |
1.09 |
1.2 |
.264 |
.076 |
300+ |
1.7 |
111 |
1.0 |
1.1 |
1% |
1.09 |
1.2 |
.299 |
.086 |
TOTAL: |
|
|
|
|
|
|
|
.124 |
.055 |
Table 4 presents the proposed stratification scheme and sample size allocation for coal mines. and the projected standard errors for estimated proportions equal to 0.5 (the projected standard errors for other proportions will be lower).
About 73% of the 1,182 coal mines were surface mines (see Table 4). Small operations with 1-9 employees accounted for 53% of surface coal mines and 28% of underground mines but accounted for only 7% and 1% of the associated employment for surface and underground mines respectively. Size differences for surface versus underground coal mines led to quite different definitions of strata by operation type.
Very large surface mines with 130 or more employees accounted for only 5% of total surface mines but employed 50% of surface workers. The sample for surface coal mines was allocated under the assumption that separate estimation capability was needed for mines with 1-9 employees, 10-29 employees, 30-49 employees, 50-129 employees, and 130 or more employees. A total of346 surface mines are expected to need to be sampled to yield 123 responding eligible mines. These mines are expected to report for 1,413 sampled employees.
Very large underground mines with 180 or more employees accounted for only 17% of total underground mines but employed 65% of underground workers. The sample for underground coal mines was allocated under the assumption that separate estimation capability was needed for mines with 1-9 employees, 10-49 employees, 50-99 employees, 100-179 employees, 180-349 employees, and 350 or more employees. A total of 298 underground mines are expected to need to be sampled to yield 195 responding eligible mines. These mines are expected to report for 1,068 sampled employees.
Table 4: Sample Allocation for Coal Mines
Stratum |
N of Mines |
Percent of Mines |
Total Number of Employees |
Percent of Total Employees |
Sample Mines |
Eligibility Rate |
Response Rate |
Responding Eligible Mines |
Average Employees Sampled Per Mine |
Total Sample Employees |
Coal Surface |
||||||||||
1-9 |
462 |
53% |
1,837 |
7% |
90 |
72% |
40% |
26 |
6 |
130 |
10-29 |
237 |
27% |
4,101 |
16% |
90 |
88% |
40% |
32 |
10 |
317 |
30-49 |
75 |
9% |
2,856 |
11% |
75 |
96% |
40% |
29 |
15 |
432 |
50-129 |
51 |
6% |
4,020 |
16% |
51 |
96% |
40% |
20 |
15 |
294 |
130+ |
40 |
5% |
12,913 |
50% |
40 |
100% |
40% |
16 |
15 |
240 |
TOTAL: |
865 |
100% |
25,727 |
100% |
346 |
|
|
123 |
|
1,413 |
Coal Underground |
||||||||||
1-9 |
88 |
28% |
353 |
1% |
88 |
65% |
40% |
23 |
7 |
114 |
10-49 |
109 |
34% |
2,522 |
9% |
90 |
73% |
40% |
26 |
10 |
263 |
50-99 |
40 |
13% |
3,088 |
11% |
40 |
88% |
40% |
14 |
15 |
211 |
100-179 |
27 |
9% |
3,699 |
13% |
27 |
100% |
40% |
11 |
15 |
162 |
180-349 |
31 |
10% |
7,855 |
28% |
31 |
100% |
40% |
12 |
15 |
186 |
350+ |
22 |
7% |
10,508 |
37% |
22 |
100% |
40% |
9 |
15 |
132 |
TOTAL: |
317 |
100% |
28,025 |
100% |
298 |
|
|
95 |
|
1,068 |
Table 4: Sample Allocation for Coal Mines (Continued)
Stratum |
Nonresponse Adjusted Mine Weight |
Average Employee Weight |
Mine DEFF |
Employee DW |
Employee ρ |
Employee DC |
Employee DEFF |
Standard Error for an Estimated Mine Proportion of .5 |
Standard Error for an Estimated Worker Proportion of . 5 |
Coal Surface |
|||||||||
1-9 |
15.8 |
13.7 |
1.0 |
1.5 |
5% |
1.2 |
1.9 |
.098 |
.060 |
10-29 |
8.8 |
16.5 |
1.0 |
1.6 |
3% |
1.3 |
2.1 |
.089 |
.040 |
30-49 |
4.6 |
14.1 |
1.0 |
1.4 |
3% |
1.3 |
1.8 |
.093 |
.034 |
50-129 |
3.3 |
21.5 |
1.0 |
1.4 |
1% |
1.1 |
1.6 |
.113 |
.037 |
130+ |
1.7 |
77.6 |
1.0 |
2.0 |
1% |
1.1 |
2.2 |
.125 |
.049 |
TOTAL: |
|
|
|
|
|
|
|
.055 |
.028 |
Coal Underground |
|||||||||
1-9 |
2.1 |
10.0 |
1.0 |
1.4 |
5% |
1.3 |
1.8 |
.105 |
.062 |
10-49 |
6.3 |
18.1 |
1.0 |
1.8 |
3% |
1.3 |
2.2 |
.098 |
.047 |
50-99 |
2.8 |
21.1 |
1.0 |
2.4 |
3% |
1.3 |
3.0 |
.133 |
.064 |
100-179 |
2.2 |
25.4 |
1.0 |
1.3 |
1% |
1.1 |
1.4 |
.152 |
.048 |
180-349 |
1.7 |
44.0 |
1.0 |
1.1 |
1% |
1.1 |
1.2 |
.142 |
.041 |
350+ |
1.7 |
100.0 |
1.0 |
1.2 |
1% |
1.1 |
1.3 |
.169 |
.051 |
TOTAL: |
|
|
|
|
|
|
|
.051 |
.025 |
The sample sizes shown in this report reflect assumptions about response and eligibility rates. For each commodity, the desired sample size is reflected by the number of responding eligible mines. Eligibility rates were estimated based upon the 2013 status of mines present in the 2013 MHSA database. These rates need to be updated for each year of each survey cycle based upon the most current MHSA. For instance, the eligibility rates for stone and for sand and gravel mines should be re-estimated based upon the 2015 status of such mines present in the 2014 database. These revised rates should be substituted into Table 2 and revised sample sizes derived for each commodity by operation type. Special effort will need to be undertaken to ensure that the desired response rate of 60% is achieved if not exceeded. Achieving this response rate will be a challenge as the survey may appear to take more time to complete than it really will.
Finally, MIWS has an entire calendar quarter as its reference period. As a consequence, MSHA Form 7000-2 employment data will be available for the entire target population of mines. These data should be used in the weighting process to identify ineligible mines, many of which may have been initially labeled as nonrespondents in the data collection process. In addition, the MSHA data provide extensive data for studying the effect of mine nonresponse on mine-level and employee-level analyses and for ameliorating this bias through poststratification adjustment to create MIWS analysis weights. Poststratification can also correct for undercoverage of new entrants to the mining population not captured in frame building.
Concluding Remarks
The sample sizes shown in this report reflect assumptions about response and eligibility rates. For each commodity, the desired sample size is reflected by the number of responding eligible mines. Special effort will need to be undertaken to ensure that the desired response rate of 40% is obtained. Achieving this response rate will be a challenge as the survey requires considerable time to complete, particularly for large, complex operations.
Finally, MIWS has an entire calendar quarter as its reference period. As a consequence, MSHA Form 7000-2 employment data will be available for the entire target population of mines. These data should be used in the weighting process to identify ineligible mines, many of which may have been initially labeled as nonrespondents in the data collection process. In addition, the MSHA data provide extensive data for studying the effect of mine nonresponse on mine-level and employee-level analyses and for ameliorating this bias through poststratification adjustment to create MIWS analysis weights. Poststratification can also correct for undercoverage of new entrants to the mining population not captured in frame building.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Rubinstein, Elaine N. (CDC/NIOSH/OMSHR) |
| File Modified | 0000-00-00 |
| File Created | 2021-01-23 |
© 2026 OMB.report | Privacy Policy