Sampling Procedures for Harvesting Sectors and references
SAMPLING PROCEDURES FOR HARVESTING SECTORS and References.docx
Regional Economic Data Collection Program for Southwest Alaska
Sampling Procedures for Harvesting Sectors and references
OMB: 0648-0722
Sampling Procedures for Harvesting Sectors1
C.1 Unequal Probability Sampling (UPS) Procedure
The objective of the vessel-level data collection proposed under this project is to estimate cost information (e.g., employment, payments to labor, and payments for non-labor inputs such as fuel cost) for each of five disaggregated harvesting vessel sectors (or vessel types) using data to be collected via a mail survey. Using ex-vessel revenue information, an unequal probability sampling (UPS) procedure will be employed to determine the sampling plan for each of the five harvesting sectors. The UPS procedure is described below. This document is an expanded version of Seung (2010).
The literature contains many methods for conducting UPS without replacement (see, for example, Brewer and Hanif 1983; Sarndal 1992). One critical weakness with most of these methods is that the variance estimation is very difficult because the structure of the 2nd order inclusion probabilities (ij)2 is complicated. One method that overcomes this problem is Poisson sampling. However, Poisson sampling has the weakness that the sample size is a random variable, which increases the variability of the estimates produced. An alternative method that is similar to Poisson sampling but overcomes this weakness is Pareto sampling (Rosen 1997)3 which yields a fixed sample size.
In this project, there are three main tasks involved in estimating the harvesting vessel population parameters (e.g., total fuel cost) using UPS without replacement for each harvesting vessel sector which lands fish at different areas [Boroughs and Census Areas (BCA) in this project]. First, the optimal sample size needs to be determined for each harvesting sector. Second, once the optimal sample size is determined, the population parameters and confidence intervals need to be estimated. Third, once the population parameters and confidence intervals are estimated for each harvesting sector (vessel type), the values of the population parameters (e.g., a harvesting sector’s total fuel cost) are allocated across different BCAs because a vessel in a harvesting sector may land raw fish at more than one BCA. The resulting numbers are a vector of total input costs for each type of vessels landing at a BCA. Confidence intervals for the population parameters are also derived in this task.
For the first task, we will use the variance of Horvitz-Thompson (HT) estimator from Poisson sampling in Part I below.4 For the second task, we will use the Pareto sampling method described in Part II below (Slanta 2006). In determining the optimal sample size in Part I, we will use information on an auxiliary variable (ex-vessel revenue). To estimate the population parameters in Part II, we use actual response sample information on the variables of interest (employment, labor income, and other input costs). For the third task (Part III below), the total cost for a certain cost category is allocated among different BCAs, using the ratio of (a) total ex-vessel revenue from landing at a BCA to (b) the total ex-vessel revenue which is an aggregation of the ex-vessel values from landings at all the BCAs in SW.
In describing the sampling procedures in Part I and Part II below, we omit the subscript for denoting the harvesting sectors because the descriptions apply to all harvesting sectors. Also, we postpone use of a subscript to denote fish landing area (BCA) until Part III because the population parameters derived from the first two parts are allocated to individual landing areas in Part III
Part I: Estimating Sample Size
Step 1: Estimation of Optimal Sample Size (n*)
Obtaining Initial Probabilities
To obtain the initial values of the inclusion probabilities (πi) for unit i in the population, we multiply the auxiliary value of unit i (Xi, i.e., the ex-vessel value of vessel i in the population) by a proportionality constant (t)5:
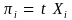 (1)
(1)
where πi : probability of vessel i being included in the survey sample
Xi : value of the auxiliary variable (ex-vessel value of vessel i in the
population)
Here, t is given by
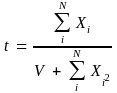 (2)
(2)
where N : population size of a harvesting sector
V : desired variance (of HT estimator of the population total); Poisson
variance. Here, V is given as:

where ε is the error
allowed by the investigator [e.g., if ε is 0.1, then 10%
error of true population total ( )
is allowed]; and z is percentile of the standard normal distribution.
Therefore, choosing a desired variance V is equivalent to setting
the values of ε and z. The value of V calculated using
)
is allowed]; and z is percentile of the standard normal distribution.
Therefore, choosing a desired variance V is equivalent to setting
the values of ε and z. The value of V calculated using
 (Poisson variance; Brewer and Hanif 1983, page 82) with πi's
being the final values of N inclusion probabilities obtained from
Step 1, will be equal to the desired variance given at the beginning
of Step 1.
(Poisson variance; Brewer and Hanif 1983, page 82) with πi's
being the final values of N inclusion probabilities obtained from
Step 1, will be equal to the desired variance given at the beginning
of Step 1.
Some of the resulting πi's could be larger than one. The number of certainty units (i.e., the number of units for which πi >1) is denoted C1. If πi > 1, then we force this inclusion probability to equal one (πi = 1).
Iterations and Determination of Optimal Sample Size
We recalculate t using the noncertainty units (i.e., the units for which πi <1) obtained in (A) above, i.e.,
 (2')
(2')
where M1 : number of noncertainty units from (A), where M1 = N – C1.
Using equation (1) above, we calculate the inclusion probabilities for the noncertainty units by multiplying the t value [from equation (2')] by the ex-vessel values of the noncertainty units. If the resulting πi's are larger than one, we force them to equal one. The resulting numbers of certainty and noncertainty units are denoted C2 ( = C1 + additional number of certainty units) and M2 ( = M1 – additional number of certainty units), respectively, where C2 + M2 = N. Next, for M2 units of noncertainty, we calculate the t and πi's again. This is an iterative process. We continue this process until the noncertainty population stabilizes (i.e., until there is no additional certainty unit).
If the noncertainty population stabilizes after kth iteration, there will be Ck units of certainty units and Mk units of noncertainty units and Ck+ Mk = N. Summing over the probabilities for all these certainty and noncertainty units, we obtain the optimal sample size (n*) as:
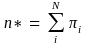 (3)
(3)
At this stage the optimal sample size may not be an integer number. In this stage, we also compute the optimal sample size under simple random sampling (SRS)6, nsrs, and compare it with n*.
Step 2: Determining Number of Mailout Surveys
Adjustment of Probabilities
Once the optimal sample size (n*) is determined in Step 1, we divide the sample size (n*) by the expected response rate (estimated based on previous surveys) to determine the number of surveys that need to be mailed out to achieve n*. The number thus derived is denoted na (this number may not still be an integer value). We next adjust the inclusion probabilities for the Mk noncertainty units obtained in Step 1 above as:
 (4)
(4)
If the resulting probabilities are larger than one (πi > 1), we make them certainties (πi = 1). The resulting numbers of certainty and noncertainty units are denoted Ck+1 and Mk+1, respectively. Next, we adjust the probabilities of the new set of noncertainty units (Mk+1) in a similar way using equation (4') below:
 (4')
(4')
We continue this process until the noncertainty population stabilizes. The resulting numbers of certainty and noncertainty units are Cq and Mq, respectively.
Apply Minimum Probability Rule
At this point, we impose a minimum probability rule. UPS can have excessively large weights (= 1/πi) and if they report a large value, then the population estimate and its variance would be very large. In order to avoid this problem, we can impose a minimum value of the inclusion probabilities. If m is the minimum imposed probability, then we do the following:
If πi < m, then set πi = m for each i, where i = 1, ..., N.
The value for m here is determined arbitrarily. The only cost involved in using this rule is a small increase in sample size.7
Finding an Integer Value for Sample Size
Next, we add up all the resulting inclusion probabilities. The resulting sum is denoted nb ( > na), which may not be an integer value. Next, we adjust again the probabilities for noncertainty units including the units for which the minimum probabilities were imposed as:
 (5)
(5)
where nc is the smallest integer value larger than nb (e.g., if nb = 15.3, then nc = 16). Finally, we add up the resulting (certainty and noncertainty) probabilities. The sum of all these probabilities is the final survey sample size (i.e., the number of surveys to be sent out to), and is denoted nm (= nc).
Part II: Estimation of Population Parameters and Confidence Intervals
Step 3: Implementation of Pareto Sampling
After the mailout sample size (nm) for each sector is determined in Step 2, the mailout sample is selected from each sector's population using Pareto sampling. The probability of each unit (vessel) being in the sample in a given sector is proportional to the unit's (vessel's) ex-vessel revenue. Because the majority of gross revenue within each sector comes from a small number of vessels, a random sample of vessels would only include a small portion of the total ex-vessel values.
According to Brewer and Hanif (1983), there are about fifty different approaches that are used for UPS. Most of these approaches suffer from the weakness that it is very hard to estimate the variance. Poisson sampling overcomes this problem, and is relatively easy to implement. However, the limitation of Poisson sampling is that the sample size is a random variable. Therefore, in this project, we will use Pareto sampling (Rosen 1997 and Saavedra 1995) which overcomes the limitation of Poisson sampling. The mailout sample size will be nm as determined in Step 2 (C) above. We will use the inclusion probabilities obtained from Equation (5) above in implementing Pareto sampling.
The procedure of this sampling method (Block and Crowe 2001) is briefly described here:
Determine the probability of selection (i) for each unit i as in Equation (5) above.
Generate a Uniform (0,1) random variable Ui for each unit i
Calculate Qi = Ui (1 – i ) / [i (1 - Ui )]
Sort units in ascending order by Qi, and select nm smallest ones in sample.
From the above, it is clear that we will have a fixed sample size with Pareto sampling.
Step 4: Mailing out Surveys and Obtaining Actual Response Sample
Next, we will send out the surveys to the nm units (vessel owners). Actual response sample will be obtained and the size of the actual response sample is denoted r.
Step 5: Estimation of Population Parameters (Population Total)
Using the information in the actual response sample, we calculate population parameters for variables of interest (e.g., employment and labor income in our project), not for ex-vessel revenue, using HT estimator (Horvitz and Thompson 1952). We are interested in estimating the population totals (not population means) of the variables of interest. The HT estimator is given as:
 (6)
(6)
where r : number of respondents
wi : weight for ith unit ( = 1/πi ). Note that the weights are calculated here
using the information on the auxiliary variable, not that on the variables
of interest
yi : response sample data of ith unit (employment or labor income)
However, the HT estimator needs to be adjusted for non-response. The estimator is adjusted in the following way.
 (7)
(7)
where N : population size
Xi : auxiliary variable of ith unit (respondents only)
Usually, we apply this adjustment to the certainties separately from the noncertainties, and then add the two together to get a final estimate. If there are no respondents within any of the two groups of certainty units and noncertainty units, then we collapse the two groups before applying the adjustment. Specifically, the final estimate of population total is given by:
 (8)
(8)
where N1 : number of certainty units in the population
N2 : number of noncertainty units in the population
r1 : number of respondents from certainty units
r2 : number of respondents from noncertainty units, and
N1 + N2 = N and r1 + r2 = r.
Step
6: Estimation of Variance for
 and
and
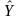
Here we will calculate the variances of the population estimates for the variables of interest. The variance estimate for Pareto sampling is given in Rosen (1997, Equation (4-11), p. 173) as:
 (9)
(9)
Since we have adjusted for nonresponse, we need to incorporate the variability due to nonresponse into the variance. If we assume that the response mechanism is fixed 8, then we have a ratio estimator and its variance can be found in Hansen, Hurwitz, and Madow (1953, page 514). This variance is a Taylor expansion, and is given as:
 (10)
(10)
where




 .
.
Step 7: Calculation of Confidence Intervals
Confidence intervals are calculated using response sample statistics obtained in steps 5 and 6. We only choose one sample, but if there were many independent samples chosen then we would expect on average that approximately 100(1-α) % of the confidence intervals constructed in the following manner will contain the average from all possible samples. The nonresponse adjustment, equation (8), is intended to bring this average from all possible estimates closer to the truth.
 (11)
(11)
where 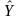 :
Estimated population total for employment or labor income.
:
Estimated population total for employment or labor income.
Note that it is possible to use t-statistics if the sample size is small.
Part III: Estimating Population Parameters and Confidence Intervals for Each Fish Landing BCA
Step 8: Allocating Costs Across Different Areas
Once
the population total (i.e., the total cost for a certain cost
category) (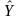 )
is obtained from Part II, in Part III, the population total is
allocated among different BCAs, using the ratio of (a) the ex-vessel
revenue from landing at a BCA to (b) the total ex-vessel revenue
which is an aggregation of the ex-vessel values from landings at all
the BCAs in SW.
)
is obtained from Part II, in Part III, the population total is
allocated among different BCAs, using the ratio of (a) the ex-vessel
revenue from landing at a BCA to (b) the total ex-vessel revenue
which is an aggregation of the ex-vessel values from landings at all
the BCAs in SW.
Let
h
(h
= 1, 2, …, H)
denote harvesting sector (where H
= 5 in our project); f
(f
= 1, 2, …, F)
cost category; a
(a
= 1, 2, …, A)
landing area. Then, the resulting cost of category f
for harvesting sector h
landing fish at an area a
denoted
 is given by:
is given by:
 (12)
(12)
where
EXVa,h
is ex-vessel value of vessel sector h
landing at a
and
 is the same as
is the same as
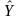 from
Part II. If, for example, there are five types of vessels and four
cost categories for each BCA. Then there will be a total of 5x4 cost
elements for each BCA. Obtaining this information is the final goal
of the above sampling work.
from
Part II. If, for example, there are five types of vessels and four
cost categories for each BCA. Then there will be a total of 5x4 cost
elements for each BCA. Obtaining this information is the final goal
of the above sampling work.
Step
9: Estimation of Variance for

EXVa,h is a constant since it comes from a non-sampled source (i.e., government data). This means that
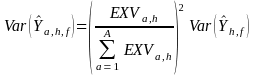 (13)
(13)
The
 is calculated using equations (9) and (10) above where yi
is the value associated with h
and f.
is calculated using equations (9) and (10) above where yi
is the value associated with h
and f.
Step 10: Calculation of Confidence Intervals
The confidence interval has the same structure as equation (11) above.
 (14)
(14)
C.2 Procedures for Estimating Population Totals and Their Reliability with Census
This section is based on Brick and Kalton (1996), Slanta (2014), and Lew et al. (2015). In some cases, the mailout sample size for a certain vessel class, which is obtained from UPS is larger than the population size. In this case, we conduct a census where we will send the surveys to all the vessel owners in the vessel class. When this is the case, the variance of the estimate is zero. The mailout sample size is equal to the population size. Since the survey is a voluntary survey, there will be some non-respondents.
The population total (e.g., total employment or total labor income for the vessel class) will be estimated simply as:
 (15)
(15)
where Xi : auxiliary variable (vessel revenue) of ith unit,
N : population size,
r : number of respondents,
yi : response sample data of ith unit (employment or labor income), and
 :
adjustment factor for non-response.
:
adjustment factor for non-response.
We will assume that a sampling unit is either always a respondent or always a non-respondent (i.e., the response mechanism is fixed). This will imply that the variance of the estimate is zero, and that confidence intervals are not available. Under this assumption, all of the error in the estimate is due to non-sampling error. Therefore we will publish the response rate in conjunction with the estimate so that the data user can have some intuitive feel for the quality of the estimate. The above assumption that the sampling unit is always a respondent or always a non-respondent is more than likely not totally true. This may be true for many sampling units, but for other sampling units the probability of responding is greater than zero and less than one. Variance formulas could be derived if these probabilities of responding were known, but since they’re not, we will assume that they are either zero or one.
To measure reliability of the population parameters for estimates where a census is conducted, we will publish both the response rate and the total quantity response rate (TQRR). TQRR in our case is defined as:
 (16)
(16)
Footnotes
In the process of developing this document, several experts in UPS sampling assisted us by providing helpful comments and inputs. The experts include John Slanta (U.S. Census Bureau), Bengt Rosen (Uppsala University), Pedro Saavedra (ORC Macro), Holmberg Anders (Statistics Sweden), Paolo Righi (ISTAT, Italy), and Bob Fay (U.S. Census). In particular, I would like to thank John Slanta very much for his time and effort in providing valuable inputs and advice. His suggestions and comments contributed significantly to the development of the sampling procedures in this document. Many thanks go to Dan Lew (NMFS) for his rigorous review and valuable suggestions which contributed in a significant way to the improvement of this document. I also benefited from discussions of UPS with Norma Sands at NWFSC and from the Excel file that she developed and from Hartman (2002).
2nd order inclusion probability (ij) is defined as the joint probability of including in sample the ith and jth population units.
Saavedra (1995) independently developed the same sampling methodology as Rosen (1997), which he called Odds Ratio Sequential Poisson Sampling (ORSPS).
Although we do not use Poisson sampling itself, we do use the Poisson variance of HT estimator of the population total.
Equation (1) is derived as follows.
HT
estimator, ,
has variance,
,
has variance,
 (Brewer and Hanif 1983, page 82) (A)
(Brewer and Hanif 1983, page 82) (A)
For an expected sample size n,
 (B)
(B)
Substituting (B) into (A) and solving for n,
 (C)
(C)
Substituting (C) into (B),
 ,
i = 1, 2, ... , N, (D)
,
i = 1, 2, ... , N, (D)
where
 is
the desired variance.
is
the desired variance.
The optimal sample size under SRS is determined using the following standard formula:
 (Levy and Lemeshow, formula
(3.14) on page 74)
(Levy and Lemeshow, formula
(3.14) on page 74)
where nsrs : optimal sample size under SRS
CVp : coefficient of variation of the population parameter. Since the
information on the population parameters (i.e., employment and
labor income) is not available, we use ex-vessel revenue, for
which the population information is available from CFEC.
Therefore, CVp is defined as standard deviation of the ex-vessel
revenue in the population divided by the mean.
This minimum probability rule is used, for example, in the Manufacturing and Construction Division of the Census Bureau. To date, there has not been any research on the minimum probability in the sampling literature. It is an arbitrary value and in applications has sometimes varied between strata in the same survey. Some researchers determine the minimum probability such that the resulting weight, which is the reciprocal of the minimum probability, is less than or equal to the population size. Generally speaking, this minimum probability rule has little effect on the sample size.
Fixed response mechanism means that a unit included in a sample is always a respondent or non-respondent no matter what sample the unit is included in. In other words, the probability of the unit being a respondent is either one or zero but nothing in-between.
References
Block, C. and Crowe, S. (2001). Pareto-ps Sampling. Unpublished Document. Statistics Canada.
Brewer, K. and Hanif, M. (1983). Sampling with Unequal Probabilities. Springer Verlag, New York.
Brick, J. and G. Kalton. 1996. Handling Missing Data in Survey Research. Statistical Methods in Medical Research 5: 215-238.
Hansen, Hurwitz, and Madow (1953). Sampling Survey Methods and Theory. Volume 1. Methods and Applications.
Hartman, J. 2002. Economic Impact Analysis of the Seafood Industry in Southeast Alaska: Importance, Personal Income, and Employment in 1994. Regional Information Report No. 5J02-07. Alaska Department of Fish and Game.
Horvitz, D. and Thompson, D. (1952). A Generalization of Sampling without replacement from a Finite Universe. Journal of American Statistical Association Vol. 47, pp. 663-685.
Levy, P. and Lemeshow, S. (1999). Sampling of Populations – Methods and Applications. Third Edition. Wiley and Sons.
Lew, D., A. Himes-Cornell, and J. Lee. 2015. Weighting and Imputation for Missing Data in a Cost and Earnings Fishery Survey. Marine Resource Economics 30 (2): 219-230.
Rosén, B. (1997). On Sampling with Probability Proportional to Size. Journal of Statistical Planning and Inference, 62, 159-191.
Särndal, C.-E., Swensson, B. & Wretman, J. (1992). Model Assisted Survey Sampling. Springer Verlag, New York.
Saavedra, P. 1995. Fixed Sample Size PPS Approximations with a Permanent Random Number. Joint Statistical Meetings, American Statistical Association, Orlando, Florida.
Seung, C. (2010). Estimating economic information for fisheries using unequal probability sampling. Fisheries Research 105(2): 134-140.
Slanta, J. (2006, 2013, 2014). Personal Communication.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Sarah Brabson |
| File Modified | 0000-00-00 |
| File Created | 2021-01-24 |
© 2026 OMB.report | Privacy Policy