ICR_Section B_1-14
ICR_Section B_1-14.docx
Rural Community Wealth and Health Care Provision Survey (RCWHCPS)
OMB: 0536-0072
ECONOMIC RESEARCH SERVICE OMB CLEARANCE PACKAGE
SECTION B. COLLECTION OF INFORMATION EMPLOYING STATISTICAL METHODS
for
CLEARANCE TO CONDUCT THE SURVEY ON RURAL COMMUNITY WEALTH AND HEALTH CARE PROVISION
FROM FY2014 THROUGH FY2015
Prepared by
Farm and Rural Household Well-Being Branch
Resource and Rural Economics Division
Economic Research Service
U.S. Department of Agriculture
January 2014
TABLE OF CONTENTS
Potential respondent universe and respondent selection methods ……………………. 1
Procedures for the collection of information …………………………………………. 6
Sample selection ……………………………………………………………… 6
Estimation procedure …………………………………………………………. 8
Degree of accuracy needed …………………………………………………... 11
Unusual problems requiring specialized sampling procedures ………………. 13
Use of periodic data collection cycles ………………………………………... 13
Methods to maximize response rates and deal with non-response issues ……………. 13
Tests of procedures or methods to be undertaken …………………………………… 15
Names and telephone numbers of people consulted on statistical methods; people who will collect the data ………………………………………………………………….. 16
Annex I. Health care facilities in the sample communities according to 2013 data from the Centers for Medicare & Medicaid Services
Annex J. Formulas for estimating means and variances
Annex L. Sample size calculation
Potential respondent universe and respondent selection methods
Provider survey
The potential respondent universe for the provider survey will include primary health care providers in rural small towns of the nine states in the study (Arkansas, Louisiana, and Mississippi – Lower Mississippi Delta (LMD) region; Kansas, Oklahoma, and Texas – Southern Great Plains (SGP) region; and Iowa, Minnesota, and Wisconsin – Upper Midwest (UMW) region). These regions and states were selected to include areas in which poverty and lack of access to rural primary care are major problems (especially in the LMD and SGP) and areas where rapid growth in employment in the health care sector has been occurring since 2002 (true in parts of all three regions), as well as areas where growth has been less rapid. The UMW region provides a contrast to the LMD and SGP regions in access to rural primary care and health care utilization, as well as in the average level of poverty and other socioeconomic and demographic characteristics. These regions also include important variations (both across and within them) in health status of the population, presence of different racial and ethnic groups, social capital and other assets, presence of retirement destination communities, programs to improve access to rural health care, and other key factors hypothesized to be related to rural health care provision.
The rural towns in the universe of this study were identified by 2000 Zip Code Tabulation Areas (ZCTAs), which are based on Zip Codes as they were defined at the time of the 2000 Population Census.1 We used ZCTAs as the primary sampling unit for this survey because this is the lowest geographic level at which data on health care access have been compiled by the Dartmouth Health Atlas2 (some of which data are used in our sampling approach), and because ZCTAs correspond closely to towns, especially in rural areas.3 We used the Rural Urban Commuting Area (RUCA) codes to classify which towns are rural, excluding towns that are part of metropolitan urban core areas (RUCA codes 1 and 1.1), suburban areas with high dependence on commuting flows (greater than 30% commuting share) to urban areas (RUCA codes 2, 2.1, 4.1, 5.1, 7.1, 8.1, 10.1), and isolated rural areas not part of a metropolitan or micropolitan core and with low commuting dependence on such areas (RUCA codes 10, 10.3, 10.4, 10.5, and 10.6).4
We included towns in ZCTAs with a 2008 population of at least 2,500 and no more than 20,000 in the universe. This focus on small towns is to ensure that the communities are large enough that recruitment and retention of primary health care providers is a realistic prospect (96% of towns with less than 2,500 population and meeting the RUCA code criteria in the study states do not have any primary care physicians) and small enough so that recruiting and retaining primary care providers is likely to be a serious problem (96% of towns with more than 20,000 population meeting the RUCA code criteria in the study states have more than 5 primary care physicians, and 97% have a hospital). We expect that recruitment and retention of health care providers is more likely to be influenced by local community assets and investments in such small rural towns than in smaller rural settlements or larger towns and cities.
The universe of small towns in the three study regions meeting these criteria includes 809 small towns with a total population of 6.1 million in 2008 (about 9% of the U.S. rural population in 2008). 51% of these towns have a hospital and 78% have at least one primary care physician, according to the Dartmouth Health Atlas data. Among the towns that have at least one primary care physician, the mean population per primary care physician is 2,275, but this ranges as high as 16,173 and as low as 233. 36% of the towns in this universe have more than 3,500 people per primary care physician, potentially classifying these as primary care Health Professional Shortage Areas (HPSAs).5
Within this universe of small rural towns, the universe of potential respondents includes primary health care providers that provide health care services in these towns. For the purposes of this study, “primary health care providers” includes licensed physicians (with either a Doctor of Medicine (MD) or Doctor of Osteopathic Medicine (DO) degree) with a primary care specialty of family practice, general practice, internal medicine, geriatric medicine, or pediatric medicine;6 dentists (with a Doctor of Dental Surgery (DDS) or Doctor of Dental Medicine (DMD) degree); physician assistants or associates (with an appropriate graduate degree such as a Master of Physician Assistant Studies (MPAS)); nurse practitioners (Registered Nurses with an appropriate graduate degree such as a Masters in Nursing); and nurse midwives (Registered Nurses with at least a Masters in Nursing and certification as a Certified Nurse Midwife (CNM)). We focus on these categories of health care providers to keep the scope of the study manageable within the budget available, yet significantly broader than most studies of rural primary health care providers (usually limited to a focus on physicians). Other categories of health care providers, such as other nurses besides nurse practitioners and nurse midwives, mental health professionals, physical therapists, and others are also important and needed in rural areas, but will be beyond the scope of this study.
We do not have the data available to list or characterize the entire population of these health care providers within the universe of 809 small rural towns identified for the sampling frame. However, as noted previously, 150 communities have been selected to be the focus of this study. (The sampling process for those communities is described in Section B.2 of this document). A list of health care providers working in each of the 150 sampled towns will be compiled using secondary sources of information and verified and revised as needed via interviews with key informants. The starting point for developing the list of providers will be the National Provider Identifier (NPI) data available from the Centers for Medicare & Medicaid Services (CMS), which are downloadable from the Internet (http://nppes.viva-it.com/NPI_Files.html) and include identifying information for all health care providers covered by the Health Insurance Portability and Accountability Act (HIPAA). The information from the NPI list will be cross checked and supplemented by at least four other types of secondary data sources, including 1) professional organization directories (e.g., the American Medical Association, American Dental Association, state directories of health care providers), 2) local health care facility websites (e.g., hospital and clinic websites), 3) other local organization websites (e.g., town or county website, Chamber of Commerce), and 4) other general sources (e.g., white or yellow pages). To be included in our provider frame, an individual provider must be verified by least two sources.
The respondents will be selected using a two stage stratified random sampling procedure. In the first stage, 150 rural small towns have been selected from six strata: the three regions x whether the town has a hospital. In the second stage, providers will be selected from the population list of providers working in these 150 sample communities, stratified by provider types. Details of the sampling procedure are provided in a subsequent section.
The expected response rate to the provider survey is 80%. The methods that will be used to maximize the response rate are discussed in a subsequent section.
Key informant semi-structured interviews
Semi-structured interviews will be conducted with key informants from each of the 150 sample communities. These key informants will be of two types: (i) administrators of health care facilities, such as hospitals and clinics; and (ii) community leaders involved or interested in recruiting and retaining health care providers.
Health care facilities and administrators will be identified using the NPI database, supplemented and verified by other secondary data sources as described in the previous section. We plan to interview up to two facility administrators (or their representatives), including the administrator of the largest hospital and the largest primary health care clinic, in communities that have these facilities. If there is no hospital and no primary health care clinic in the community, we will seek to identify and interview up to two knowledgeable individuals who are involved in the health care industry in another way, such as public health, nursing care facilities, or other community health-related programs.7
We will also seek to interview up to two community leaders in each town. Relevant community leaders will be verified or identified by contacting the chief executive officer of the town (i.e., the mayor or town manager), and by asking administrators of health care facilities for names of community leaders involved in health care issues. In addition to town mayors or managers, likely participants could include people involved in economic development or other local government or non-profit organizations.
Due to the widely varying situations in small communities, appropriate key informants may need to be identified on a case-by-case basis, following the preferred protocols to the extent possible. In particularly small communities with no local health care available, it may be necessary to contact key informants at the county level for some types of information.
The expected response rate to the key informant semi-structured interviews is 67%.
Procedures for the collection of information
Sample selection
Sample community selection
The number of sample communities was calculated to ensure a margin of error of no more than 0.05 in measuring proportions in the provider survey, such as the proportion of respondents who felt that the quality of local schools was an important factor influencing their decision to work in the community. The sample size calculation is shown in Annex L.
The 150 sample towns have been selected using a stratified random sample. Six strata were used: the three study regions (LMD, SGP, UMW) x whether or not the town has a hospital. The allocation of the sample among the strata was based on minimizing the variance in the number of primary care physicians per population, which is expected to be strongly correlated with most of the variables investigated in the survey (e.g., local factors affecting health care provision, availability and quality of health care). Within each stratum, systematic sampling with a random start was used, with the list of towns sorted by two variables: a variable based on ranges of the number of primary care physicians in the towns, and the population size of the town. The use of systematic sampling with a random start produces unbiased and consistent estimates of population parameters and is more efficient than simple random sampling if the variables used to sort the sample are correlated with the response variables.8
Of the 150 sample communities, 12 will be selected for inclusion in the pilot phase of the study, as noted in Part A. Two of these 12 communities will be randomly selected from each of the different strata discussed above. The data collected from the pilot phase communities will be combined with the data collected from the remaining 138 sample communities in the analysis of results, except for survey questions that are revised or dropped as a result of the pilot study.
Provider survey respondents
The sample of respondent health care providers within each sample town will be selected using a stratified simple random sample, in which the types of providers are the three strata (i.e., physicians, dentists, and other providers (physician assistants, nurse practitioners, and certified nurse midwives), each as one stratum). The number selected within each stratum will be roughly proportional to the total number of providers in that stratum working in the town, and the total number selected will be limited to a maximum of 8. If there are 8 or fewer providers working in the town, a complete census of providers will be interviewed. The reason for limiting the sample to a maximum of 8 providers per sample community is to limit the cost of the survey and the burden on members of any particular town, while allowing a sufficient number of observations to be representative of the providers in the town. A complete census of all providers within every town is not necessary for the purposes of this study, and would not be efficient because the information collected from multiple providers in the same town is not likely to be completely independent.9
Considering the maximum sample of 8 health care providers per sample community, and the expected response rate of 80%, the maximum number of potential respondents in the 150 sample communities is 1500 (150 x 8/80%).
Key informants
As noted above, we will seek to interview up to four key informants per sample community; two health care facility administrators and two community leaders. Considering the expected response rate of 67%, the maximum number of potential respondents to the key informant interviews is 900 (150 x 4/67%).
Estimation procedure
The sample means and variances of the quantitative survey response variables will be estimated using the formulas provided in Annex J, which reflect the complex two stage sample design. Comparisons of means of different subpopulations (e.g., communities with vs. without a hospital, communities in different regions) will be based on the formula (which follows from the Central Limit Theorem):
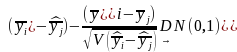 ,
,
where
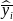 and
and
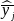 are the sample means of y in subpopulations I and J,
respectively (with
are the sample means of y in subpopulations I and J,
respectively (with
 );
);
 and
and
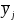 are the subpopulation means of y in subpopulations I
and J;
are the subpopulation means of y in subpopulations I
and J;
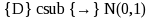 means “converges in distribution to a standard normal
distribution”; and V( ) denotes the variance operator.
means “converges in distribution to a standard normal
distribution”; and V( ) denotes the variance operator.
The variance of the difference in subpopulation means is estimated by the formula:
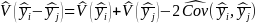 ,
,
where
 refer to the estimated variance and covariance, respectively.
refer to the estimated variance and covariance, respectively.
In cases where the subpopulations being compared are sampled independently, such as when they are from separate strata (e.g., if comparing communities with vs. without a hospital or communities in different regions), the covariance term in equation 2) is zero, simplifying the estimation. To compare subpopulations that are not from separate strata, multiple regression analysis will be used to account for covariance among the subpopulations.
An equivalent procedure to estimate the differences in means between subpopulations is to use an ordinary least squares (OLS) regression, with dummy categorical variables for each of the subpopulations except one (and using the appropriate estimators of the regression coefficients and variance matrix to reflect the complex sample design).10 The coefficients of each of these dummy variables represent the difference in means between the subpopulation represented by the dummy variable and the excluded category.
The analysis using OLS regression will be extended to include other observed covariates (x) (some of which will come from other available data sources) that are expected to be correlated with the y variables (e.g., population size of the community; proximity to a metropolitan area, a highway, or natural amenities) as explanatory variables. There are three purposes of this extension: 1) to account for the influence of other potentially confounding factors on the differences that are being estimated (e.g., accounting for the fact that differences in mean responses between communities with vs. without a hospital may be due to differences in their population size, access to a city or other factors); 2) to investigate the effects on the response variables of these other factors, many of which represent different types of assets and whose influence are part of the study objectives; and 3) to reduce the residual unexplained variance, which will improve the efficiency of the estimated differences between target subpopulations.
One drawback of using OLS regressions to estimate the effects of factors on a binary response variable is that the predicted mean values of the response variable can be outside of the range of feasible values; i.e., greater than 1 or less than 0. Maximum likelihood discrete choice models, such as probit and logit models, are superior in this regard.11 Hence we will also use probit models to estimate the influence of covariates on the probability of a positive response for binary response variables.12 For multiple valued ordered response variables, ordered probit models will be used. Almost all of the response variables collected in the survey will be either binary or ordered variables, so these models will be commonly used.
Degree of accuracy needed
We seek to answer the research questions with the greatest possible accuracy, and the sampling approach has been designed with this objective in mind. We illustrate the statistical power to answer research question 1. Similar results apply for the other research questions.
Research question 1 asks about the importance of different factors that may have influenced health care providers’ decision to practice in a particular town. This question is addressed by Question 21 in the health care providers’ questionnaire. The question asks about several factors, and asks the respondent to rate the importance of each factor on a scale from 1 (not at all important) to 5 (very important). Although this is a five point scale, it can be summarized by a set of binary response variables. For example, one binary response could be whether the factor is moderately or very important (response is at least 4 or not).
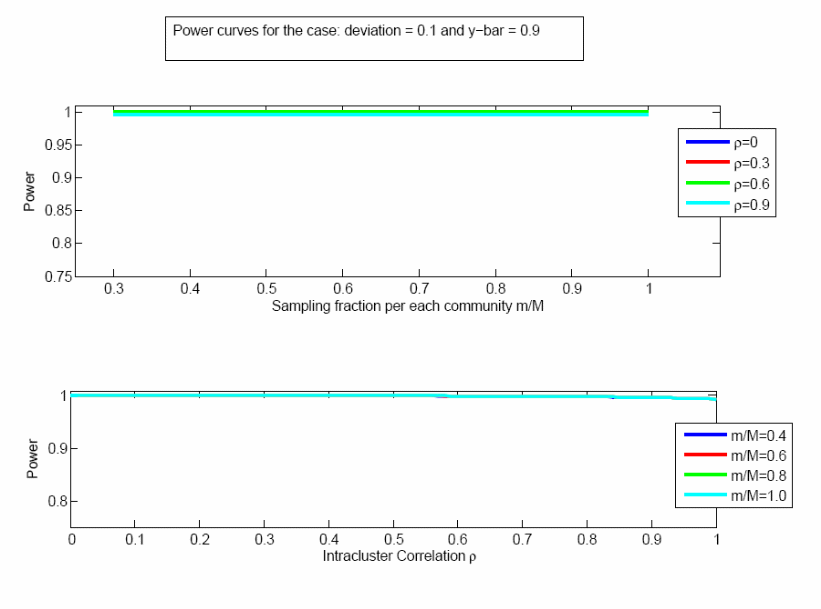
The power calculation depends upon the sample size, the population size, the true population mean being estimated, the effect size, and the correlation between responses within a community (the “intra-cluster correlation coefficient”). We seek to detect an effect size of 0.10; e.g., a difference between a null hypothesis that 50% of the provider population considers the size of the town at least moderately important, and an alternative hypothesis that at least 60% of this population considers that factor at least moderately important. The power to detect such a difference is shown in Figures 1 and 2, as a function of different levels of the intra-cluster correlation coefficient (ρ), the sampling fraction within each community (m/M), and the true population proportion (0.5 or 0.9). The results are insensitive to the sampling fraction but more sensitive to ρ, and in almost all cases the power is greater than 90%. Even with the extreme case of ρ = 1, which we do not expect, the power is greater than 75%.
Figure 1. Power analysis when the true population mean is 0.5, effect size is 0.1.
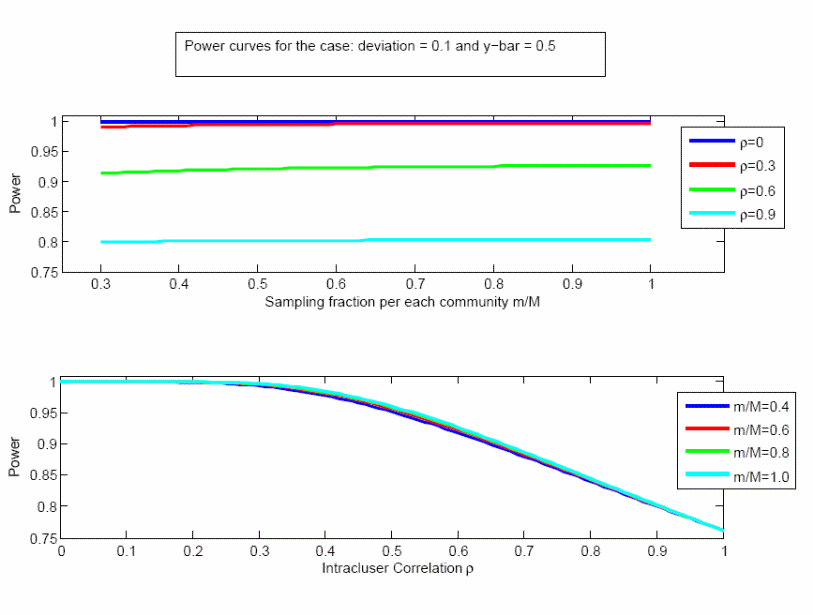
Figure 2. Power analysis when the true population mean is 0.9, effect size is 0.1.
Unusual problems requiring specialized sampling procedures
There are no unusual problems requiring specialized sampling procedures.
Use of periodic data collection cycles
Not applicable; this is a one-time data collection effort.
Methods to maximize response rates and deal with non-response issues
Several research procedures will be incorporated to maximize the mail/web survey response rate. Potential respondents will be provided with advance information about the project from a variety of sources. Notices and/or articles about the upcoming project will be placed in several applicable publications, such as the Journal of Rural Health and Rural Roads magazine, and on websites such as RuralHealthWeb.org and the National Rural Health Association website. Advance letters and a colorful informative sheet/brochure will be sent to sampled individuals prior to the paper survey mailing. A project website will be available with additional information, and a toll-free number will be provided for those who have questions or concerns. Potential respondents will be advised that project results will be available to them and other members of their community through the project website within 6 months after the completion of data collection.
Operationally, limited samples will be drawn from the frame, with replicates added only as necessary. A paper copy of the survey will be mailed to sampled providers along with a cover letter and instructions for accessing the survey online if they choose. A second copy of the survey and instructions for online access will be sent to non-respondents after an appropriate time span, followed by reminder telephone calls as needed. Respondents who are unable or unwilling to complete the mail or web survey will also have the option to complete it by telephone.
The pilot study in 12 communities will be particularly useful in identifying and evaluating any potential response rate and non-response issues. Should any such problems arise during the pilot study, procedures can be adapted to address the issues at hand so that response rates for the ensuing 138 communities will be maximized.
We have a target response rate of 80% and believe that this target is achievable based upon similar surveys conducted by the Survey and Behavioral Research Services (SBRS) group at Iowa State University – the organization that will implement the survey. In 2009, SBRS completed data collection for a community-based study that focused on the impact of the retail sector in small rural communities (Community Resiliency: Role of the Retail Sector in Easing Sudden and Slow Motion Economic Shocks). A sample of 32 communities in 8 states was chosen, and a total of 1,161 interviews were conducted with retail business owners, community leaders, and community residents (general population). The sample for the retail owners and community leaders was developed in a manner similar to the process for the proposed project. The response rate for the community leaders was 76.4%, with a 61.8% response rate for the retail business owners. For the proposed project, it is expected that the response rate will exceed that of the Community Resiliency project and could reach the target of 80%, given the significant follow-up measures planned (more than in the Community Resiliency project) and the high saliency of the topic (health care in rural communities) for the respondents.
If the unit response rate in the pilot study is less than 80 percent, an investigation of potential nonresponse bias will be planned and implemented in the full survey, using data available from secondary sources, the sample frame, and the survey. For example, we could investigate whether potential respondents having higher expected salaries were less likely to participate as respondents in the survey (due to higher opportunity costs of their time). The analysis in this example would combine data from secondary sources such as the Bureau of Labor Statistics on salary ranges existing for particular health care occupations in particular locations, information from the sample frame on the location and specific occupations of the potential respondents, and information from the survey on which potential respondents decided not to participate. Data from the survey could also be used to investigate the extent to which the responses to key survey questions – such as the importance of different types of community assets in affecting health care providers’ decisions to work in the community – differ between respondents from different occupational groups or different locations. Combining these types of analysis will enable an assessment of the two components of non-response bias: i) differences between respondents and non-respondents in characteristics hypothesized to influence response variables of interest; and ii) the extent to which such characteristics are correlated with the response variables of interest.
Tests of procedures or methods to be undertaken
The pilot study will be used to evaluate the survey protocol (e.g., the procedures used to identify, inform and contact respondents, schedule interviews, etc.) and to estimate the response rates for individual questions and the unit response to the survey as a whole. If the response rate is below 70 percent for individual questions, these questions will be revised to improve response rates or dropped in the full survey. If the response rate to the pilot survey as a whole is below 80 percent, efforts to maximize the response rate will be applied to the fullest extent possible, and an investigation of nonresponse bias will be conducted, as described in the preceding section.
Names and telephone numbers of people consulted on statistical methods; people who will collect the data
-
Name
Position
Telephone
Cindy Yu, PhD
Project Statistician, Assistant Professor of Statistics, Iowa State University
515-294-6885
Sarah Nusser, Ph.D.
Professor of Statistics, Iowa State University
515-294-9773
Shirley Huck
Assistant Director, Survey & Behavioral Research Services (SBRS), Iowa State University
515-294-1652
Janice Larson
SBRS Survey Unit Director
515-294-3451
Allison Anderson
SBRS Project Manager
515-294-1949
Jody Fox
SBRS Data Collection Supervisor
515-294-4289
Debbie Bahr
SBRS Data Collection Supervisor
515-294-3104
Anthony Connor
SBRS Programmer & Data Manager
515-294-6211
Cathy Owen
SBRS Database Manager
515-294-5346
Sue Thomas
SBRS Data Collector
515-294-5242
1 ZCTAs are defined and data on them are available at the Census Bureau website: http://www.census.gov/geo/ZCTA/zcta.html..
2 Information on the Dartmouth Health Atlas and downloadable health sector data are available at http://www.dartmouthatlas.org/.
3 Larger towns sometimes include more than one ZCTA. In these cases, we combined these ZCTAs into a single town for the purposes of selecting the sample. Henceforth we refer to the primary sampling unit as “towns”.
4 Information on RUCA codes is available at: http://www.ers.usda.gov/data-products/rural-urban-commuting-area-codes/documentation.aspx
5 Other criteria besides the population per number of primary care physicians are also considered in designating primary care HPSAs: http://bhpr.hrsa.gov/shortage/hpsas/designationcriteria/primarycarehpsacriteria.html.
6 This definition of primary care specialties is based upon definitions used by Medicare. See: http://www.medicare.gov/physiciancompare/staticpages/resources/specialtydefinitions.html.
7 Analysis of National Provider Identifier (NPI) data available from the Centers for Medicare & Medicaid Services (CMS) indicates that 28 of the sample communities have no hospital or clinic, that the maximum number of hospitals in any of the sample towns is 3, and that the maximum number of clinics is 10 (Annex I).
8 If the variables used to sort the sample are uncorrelated with the variables of interest and the sort order is random, systematic sampling and simple random sampling are of similar efficiency (see Särndal, et al. (2003), section 3.4).
9 We discuss the issue of non-independence and its implications for sampling efficiency further in a subsequent subsection.
10 Appropriate regression estimators for complex two stage sample designs are available in the software program Stata, which will be used for the analysis. The variance estimator used by Stata assumes a stratified simple random sample in the first stage, which yields a conservative estimate of the variance for the case of a stratified systematic sample (which we are using in the first stage).
11 Furthermore, if the distribution function assumed in the maximum likelihood model is the correct one, maximum likelihood is the most efficient estimator. However, violations of distributional assumptions, which can’t be tested in binary response models, can cause maximum likelihood estimators to be inconsistent and inefficient. See Maddala (1983) for a discussion of maximum likelihood discrete choice and ordered response models.
12 The difference between a probit and logit model is in the univariate distribution function assumed in the maximum likelihood model (normal vs. logistic). In practice, the results of these models are quite similar.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | %USERNAME% |
| File Modified | 0000-00-00 |
| File Created | 2021-01-26 |
© 2026 OMB.report | Privacy Policy