CE 4.4.3 OMB Clearance Supporting Statement B 1-14-14
CE 4.4.3 OMB Clearance Supporting Statement B 1-14-14.docx
Evaluating the Retired Mentors for Teachers Program
OMB: 1850-0908
Prepared For:
Institute of Education Sciences United States Department of Education Contract No. ED IES-12C-0007
Prepared By: REL Central Regional Educational Laboratory
September 16, 2013
|
||
|
||
|
||
Submitted to: Submitted by: Institutes of Education Sciences REL Central U.S. Department of Education 9000 E. Nichols Ave., Ste. 112 555 New Jersey Ave., NW Centennial, CO 80112 Washington, DC 20208 (303) 766-9199 (202) 219-1385
Project Officer: Project Director: Ok-Choon Park Dale M. DeCesare |
||
|
Table of Contents
Section B. Data Collection Procedures and Statistical Methods 2
B1. Respondent Universe and Sampling Methods 2
B2. Procedures for the Collection of Information 4
B3. Methods to Maximize Response Rates and To Deal With Non-Response 7
B4. Tests of Procedures or Methods to be Undertaken 8
B5. Individuals Consulted on Statistical Aspects of the Design 9
Section B. Data Collection Procedures and Statistical Methods
The U.S. Department of Education (ED) requests OMB clearance for data collection related to the Regional Educational Laboratory (REL) program. ED, in consultation with REL Central under contract ED-IES-11-R-0036, has planned a study of a program that uses retired master educators to provide mentoring support to probationary teachers (in their first three years with the district) in high need elementary schools in Colorado’s Aurora Public School District (APS). This program is referred to as the “Retired Mentors for New Teachers Program.” OMB approval is being requested for REL Central’s data collection for this project, including a REL Central teacher survey and multiple focus groups conducted by REL Central of mentee teachers and mentors in the program.
The study will also draw upon several types of data that the district collects. These include teacher turnover rates in high-need elementary schools, data from school administrator evaluations of teacher performance, mentor records of support, and student assessment scores for students served by teachers in participating elementary schools. OMB approval is not being sought for this turnover, evaluation, and assessment data since these are collected by the district and not REL Central.
B1. Respondent Universe and Sampling Methods
The selection of APS as a target district was guided by several considerations. First, as part of the REL Central contract, the focus of the study is the Central Region, which includes Colorado where the target school district is located. Second, since growing numbers of schools and districts across the region work to serve increasing populations of at-risk students, REL Central sought to implement the intervention in a school district with relatively high levels of student need that are seeking ways to close the achievement gap. APS meets this target, since approximately 70 percent of the district’s student population receives free or reduced-price lunch. The target schools also are high-need, and all will have at least 50 percent of their student population eligible to receive free or reduced-price lunch. Third, by conducting the study within a single, large district the study can minimize variations in curriculum, testing, induction, or other characteristics that might come into play if several smaller districts were instead included in the analysis. Lastly, by concentrating recruitment in a large district with high numbers of at-risk students, the study is able to recruit schools while keeping the cost of implementation and research activities manageable.
The study will focus on core subject probationary teachers (those in their first 3 years with the district) in grades 1–5 in a sample of high-need elementary schools. We focus on probationary teachers because the intervention targets those teachers new to the profession or to the district. Grades 1–5 in core subjects were selected based on the availability in the district use of the MAP Assessment in reading and math in these grades.
The potential sample of teachers includes grades 1–5 core academic probationary teachers in their first 3 years at the district (presently estimated at 100 teachers: 50 treatment and 50 control) in 12 high-need elementary schools in the Aurora Public School District (APS) in Aurora, Colorado. APS is the third largest district in Colorado and has close to 60 schools. APS is also one of the highest-need school districts in the state, with 71 percent of its students overall eligible to receive federal free or reduced price lunch. The district has 27 P-5 elementary schools and five P-8 or K-8 schools.
Participating schools will be selected to include schools that serve at least 50 percent of students who qualify for free or reduced-price lunch, which is a proxy frequently used for determining the proportion of students deemed at-risk of failure in school. The universe of students that will be included in the study is all grades 1–5 students enrolled in the target group of elementary schools. The district will work with the REL Central team to ensure that appropriate numbers of probationary teachers are available to participate in grades 1–5 to meet sample size requirements (see Section B2 below addressing statistical power).
Teachers will be randomly assigned within each school so that each participating school will have some of its probationary teachers receive the intervention. Randomly assigning teachers within schools best utilizes the limited resources available for delivering the intervention in terms of sample size and statistical power. Random assignment at the school level would require a prohibitive number of schools in order to achieve the desired statistical power. Aurora Public Schools has a limited number of elementary schools that meet the eligibility requirements and these are insufficient to provide adequate statistical power if schools were the unit of random assignment. Randomly assigning teachers within schools also complies with the desires expressed by district leaders that each participating school site should have the opportunity to receive at least some support from the intervention. If random assignment were conducted at the school level, schools assigned to the control group would receive no added support for their teachers during the course of this study.
It is not anticipated that the intervention can have any effect on student assignments in year 1 since teachers will be randomly assigned to receive the added mentoring, and REL Central anticipates principals will not be notified about the results of this assignment until after student classroom assignments have already been determined. In any event, for both years 1 and 2, REL Central will communicate with principals in each school regarding the importance of maintaining fidelity to the research project in order to help the district understand whether the intervention is truly effective and a worthwhile investment of limited district resources.
For this multi-site cluster randomized trial, random assignment of teachers will proceed as follows. First, each teacher will be assigned a random number from 0 to 1.0000 via a random-number generator. Next the teachers will be sorted by school, then within school by the grade level they will teach, and then within grade level by the random number.
The first teacher in the list will then be assigned to an experimental group based on a new randomly generated number. If this random number is between 0 and 0.5000, they will be assigned to the treatment group. They will be assigned to the control group if the random number is between 0.5001 and 1.000.
Assignment of the remaining teachers within each school will proceed as follows. Moving down the list of teachers (sorted by school, grade level, and first random number), teachers will be alternatively assigned to the other experimental group. When moving down the list, the order of assignment will always remain the same, based on the initial teacher assignment. Control will always follow treatment, and treatment will always follow control. For example, if the first teacher is randomly assigned to the control group, then the second teacher on the list will be assigned to the treatment group, the third teacher to the control group, the fourth teacher to the treatment group, and so on.
B2. Procedures for the Collection of Information
Power analyses were conducted to estimate the sample size necessary to achieve the desired statistical power of greater than 0.80 to reject the null hypothesis of no difference between the treatment and control groups on the student achievement outcomes using two-tailed tests with an alpha level of .05. Parameters used in the power analyses and the rationale for their values follow.
We estimated the statistical power of two values for the assumed minimally-detectable effect size of the intervention: a value of 0.20 standard deviation and a value of .25 standard deviation on the student achievement outcomes. This decision is based on the following. First, research in the area of teacher induction has found similar effects. Glazerman, et al. (2010) found effects of .20 for math and .11 for reading after two years of implementation of a comprehensive teacher induction program. The Glazerman, et al. study included a large sample across a number of different districts. Student achievement was measured using a variety of standardized test data administered by and obtained from the participating districts.
In addition to the Glazerman, et al. study (2010), we draw on results of a review of studies of professional development. Yoon, et al. (2007) found the average effect of professional development programs was 0.53 standard deviations or 21 percentile points in terms of student achievement in the nine studies that met the IES What Works Clearinghouse (WWC) evidence standards. Although the studies included in the calculation of the effect size evaluated a variety of professional development programs, the results suggest that professional development can lead to impacts on student achievement. In the studies reviewed, teachers received an average of 49 hours of professional development. This dosage compares with the 54 to 72 hours per year for the intervention we propose to examine.
Our decision to estimate the sample needed to detect an effect of between 0.20 and 0.25 also considered that this size effect represents a non-trivial increase in student achievement. Effect sizes in this range translate into an improvement index of between 8 to 10 percentile points, which can be interpreted as an 8 to 10 percent increase in percentile rank, on average, for comparison group students should they have been taught by teachers offered the intervention. The conversion of an effect size expressed in standard deviation units (for example, Hedges’ g) to a difference in percentile rank is a mathematical conversion based on the area under the normal curve. This conversion is not specific to any test, outcome, or grade level nor does it vary by any test, outcome, or grade level (Lipsey, et al. 2012; What Works Clearinghouse, 2011).
Our goal was not to estimate the sample size needed to detect any difference between the treatment and control groups because that would be prohibitive in terms of sample size and resources. Our goal, instead, was to estimate the sample size needed to provide adequate statistical power to detect a difference that might be expected given the empirical findings for similar interventions and that represent a meaningful improvement in student achievement. Our arrival of effect sizes between 0.20 to 0.25 standard deviations reflects this approach.
Data collected on educational environment has multiple sources of variation due to nested structure of the school environment, such as students within classrooms. The intra-class correlation (ICC) is a measure of the proportion of total variance that is between groups of students. The ICC is important to power analyses because statistical power decreases as the ICC increases. We drew on empirical results from studies similar to the proposed study (i.e., studies that used teachers as the unit of random assignment) to inform our assumptions regarding the value for the ICC to use in our analyses. These empirical results for ICC are as follows. Apthorp, et al. (2012) reported intraclass correlations of 0.12, 0.14, 0.13, and 0.20 at the classroom level for Grade 3 and 4 vocabulary outcomes. Constantine, et al. (2009) had an ICC of 0.16 for elementary grades using reading and mathematics outcomes. Drummond, et al. (2011) reported 0.04 for Grade 6 reading comprehension. Hitchcock, et al. (2011) found a classroom ICC of 0.09 at Grade 5 for reading comprehension. Wijekumar, et al. (2009) reported a classroom ICC of 0.07 for Grade 4 mathematics. Based on these empirical estimates, we used an interclass correlation of 0.20 as a conservative estimate of the ICC for our power analyses.
Another important parameter for the power analysis was the estimated proportion of variance in the outcome explained by covariates. As with the effect size and ICC, prior research informed our decision. A range of values have been reported in the literature for R-squared, typically examining power for designs that randomize whole schools and that use pretest covariates lagged at least one entire calendar year (Bloom, Bos & Lee, 1999; Bloom, Richburg-Hayes & Black, 2007; Hedges & Hedberg, 2007; Schochet, 2008). An R-squared of 0.75 was used as a conservative estimate of the proportion of variance explained by the covariates assuming an increase in precision from aggregating test scores at the classroom level and using pretests from the fall and posttests from the spring of the same school year.
In addition to the above parameters, we assumed 20 students in each classroom would be included in the impact analysis sample after accounting for student-level attrition. This assumption is conservative and takes into account the mobility rate for the target district (approximately 30 percent) and the average class size among the elementary schools within the target district that is approximately 30 students per classroom.
We propose a multi-site cluster randomized trial where teachers are randomly assigned to the intervention within school. Power analyses for this multi-site trial included two additional parameters. First, we assumed a conservative 5 percent of variance accounted for in the post-test by the blocking variable because we anticipate that the vast majority of variation in student achievement is between students and within schools rather than between schools. Second, the power analysis needs to account for the analytic approach to estimating effect size variance between clusters (that is, classrooms). We conducted the power analysis to estimate the sample size needed for both a fixed effect approach (no estimation of the variation in effects between clusters) and a random effects approach with an assumed variation between clusters of 0.01. We believe that the fixed effects approach is justifiable given that generalizing the results to other contexts is not the only purpose of this study. For instance, one purpose is to estimate the impact of the teacher mentor program within Aurora Public Schools. Aurora seeks to understand the impact of the intervention as a whole and to use this information to inform its decision regarding further investment of resources toward a wider implementation of the intervention. Some variance in the intervention’s impact between teachers is expected, but an estimation of this variance is not critical to the district in order to guide its future decisions.
Power was calculated using the Optimal Design software, version 3.0 (Spybrook, et al., 2011). Statistical power was estimated for a multi-site trial design for continuous outcomes with the treatment at Level 2. Power analysis was run to estimate the statistical power that would be provided by our current estimate of the number of participating schools (14) and the number of participation teachers after accounting for 20% attrition, for an average of six teachers per school. This approach was used to account for random assignment of teachers within schools, a conservative estimate of teacher attrition , and the blocking of teachers within school for random assignment.
Results of the power analysis are shown in Figure 1. Given the parameter described above, the statistical power for detecting an effect of 0.25 would be 0.96 in a fixed effect model and 0.89 in a random effects model. The statistical power for detecting an effect of 0.20 would be 0.84 using a fixed effects approach and 0.73 for a random effects approach.
Our assumption for teacher attrition is conservative and mainly applies to the Year 2 sample, because we anticipate that most teacher attrition will occur between Year 1 and Year 2. Statistical power for detecting effect sizes mentioned above will likely be higher for Year 1. In addition, we will work closely with the district to maximize the participation of schools and teachers in order to maximize statistical power for detecting effects after Year 2.
This study uses a purposive sample; no plans are in place to weight the sample to represent subgroups.
Figure 1. Statistical Power Curve
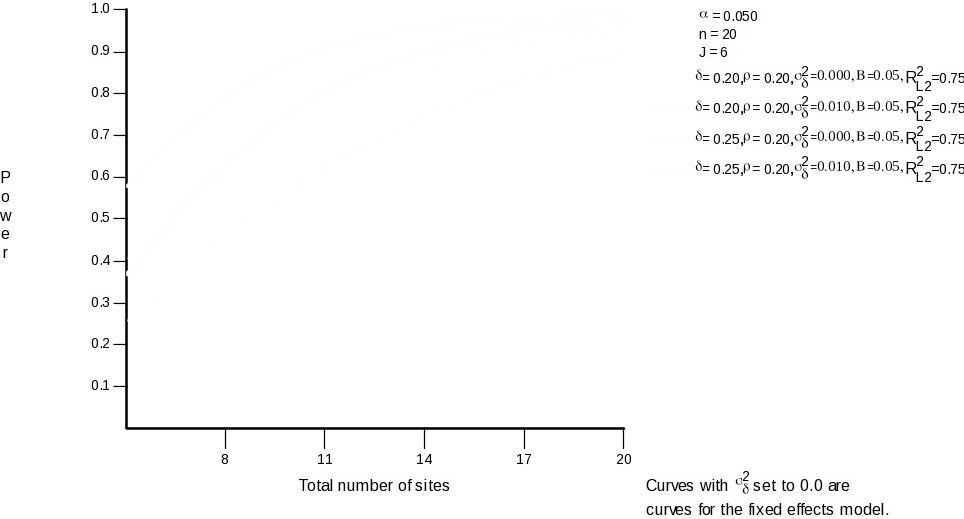
B3. Methods to Maximize Response Rates and To Deal With Non-Response
Non-response with regard to district data collection (such as student test scores, teacher turnover data, and teacher evaluation data) is not expected to be an issue for the study. The district supports the study’s need to conduct pre- and post-assessments at the beginning and end of each school year. The district has dedicated resources in its assessment office to provide training and remuneration for test proctors and to support schools in implementing such pre- and post assessments. This support removes any burden of assessment administration from the participating teachers. In addition, the assessments are administered online, so there will be minimal disruption to the participating teachers’ classrooms and instruction. The district assessment office routinely collects assessment data, and has agreed to share this data with REL Central. REL Central therefore does not anticipate difficulty in obtaining this data. Similarly, teacher turnover and evaluation data is collected routinely by the district.
Requests for data from the district will be made two weeks prior to the due date for providing such data through a phone call. The phone call will be followed up with an email a week prior to the due date. If data is not provided by the due date, REL Central will follow-up with a telephone call to non-responding individuals. Data requests will maintain consistency in the format with which data is requested.
Researchers will seek to obtain an 80% or higher response rate to surveys, as suggested by the Office of Management and Budget (2006). We will seek to obtain not only an overall 80% response rate but also a response rate of 80% from teachers in the control and treatment groups. We will report on the differential response rate between the control and treatment groups, if it occurs. In order to maximize the response rate, we will employ techniques identified in the tailored design survey methods (Dillman, 2000). This will include repeated contacts with teachers using different formats, such as in-person reminders from the retired mentor in each school and email reminders. REL Central will also request that school principals send a brief email to encourage teachers to take the survey (see Attachment F).
We will also minimize the burden on participants by:
Working with educators to determine a time to administer the survey that would allow for greater response;
Using web-based surveys that allow the respondent to complete the survey at a time and place of their choosing;
Offering a paper-based version of the survey on request;
Designing a survey that is easily understood;
Working through the retired mentor and principal at each school site to advocate for teachers to complete the survey; and
Providing a direct link in email correspondence that will take respondents directly to the survey instrument.
Teachers will be invited to attend an in-person meeting in which consent forms will be collected; therefore, teachers will provide consent to participate prior to receiving the survey. At the meeting, teachers will be provided with information on the procedures for collecting data, including information about how the researchers will protect the confidential data. This information will also be included on the consent form (see Attachment D).
Researchers will also send targeted email reminders in order to increase the response rate (see Attachments G and H). Additionally, teachers will be offered an incentive of $25 from the school district to complete a survey as part of the study. This incentive is based on the district’s policy for compensating teachers for time outside of their regular contract hours.
Similar incentives and techniques will be used to encourage and support teacher participation in focus groups. A $25 stipend will be provided to each focus group participant. Participants will receive multiple contacts informing them of the stipend and encouraging them to participate in the focus group, including in-person contacts from the retired mentor at each school and email reminders. Retired mentors will work with mentees and principals at each school site to help identify the most convenient location, time of day, and day of the week for teachers to be able to participate in a focus group.
B4. Tests of Procedures or Methods to be Undertaken
In June 2013, researchers conducted a pretest of the survey instrument with six teachers. The pretest was used to gather data to refine the survey and assess reliability and validity. This refined survey will be used to conduct the full study in the 2013–2014 and 2014-2015 school years.
The pretest was administered electronically. Teachers were sent an email with instructions for participating in the pilot and a link to the survey instrument online. Teachers were asked to note the time that they started and finished the survey to gain an accurate estimate of the amount of time needed to take the survey. Following their completion of the online survey, teachers in the pretest were asked to answer the following questions:
How long did the survey take to complete?
Are the directions clear?
Are there any words or language in the instrument that teachers might not understand?
Is there anything you would change about the instrument?
What problems, if any, did you have completing the survey?
Feedback from the pretest indicated that respondents had no problems with the directions or language in the instrument. Respondents did not indicate any problems in completing the survey or that any changes to the instrument were needed. One respondent indicated the addition of a “progress completion” bar would be useful and this feature was added to the survey. One respondent also suggested breaking one of the longer survey questions into two parts, and this suggestion is incorporated into the final survey version. Survey respondents were asked to pretend that they were in the treatment group in order to complete all survey questions. Respondents indicated a range of 6–10 minutes needed to complete the survey. To be conservative, we estimate 20 minutes needed to complete the full survey.
B5. Individuals Consulted on Statistical Aspects of the Design
The following individuals were consulted on the statistical, data collection, and analytic aspects of this study:
Name |
Title |
Organization |
Contact Information |
Dr. Trudy Cherasaro |
Co-Principal Investigator |
Marzano Research Laboratory |
trudy.cherasaro@marzanoresearch.com 303-766-9199 |
Dr. Linda Damon |
Technical Work Group Advisor |
Retired Director of Professional Learning |
|
Dale DeCesare, Esq. |
Co-Principal Investigator |
APA Consulting |
720-227-0089 |
Dr. Bob Palaich |
President |
APA Consulting |
720-227-0072 |
Dr. Bruce Randel |
Technical Work Group (TWG) Member |
Century Analytics |
bruce.randel@centuryanalytics.com 303-842-9607
|
Dr. Michelle Reininger, |
Technical Work Group (TWG) Member |
Assistant Professor Stanford University and Executive Director of the Stanford Center for Education Policy Analysis |
(650) 725-4101 |
Justin Silverstein |
Vice President |
APA Consulting |
720-227-0075 |
The following individuals will be involved in the study implementation:
Name |
Role |
Organization |
Contact Information |
Dale DeCesare, Esq. |
Co-Principal Investigator |
APA Consulting |
720-227-0089 |
Dr. Trudy Cherasaro |
Co-Principal Investigator |
Marzano Research Laboratory |
trudy.cherasaro@marzanoresearch.com 303-766-9199 |
Dr. Bob Palaich |
President |
APA Consulting |
720-227-0072 |
Dr. Linda Damon |
Technical Work Group Advisor |
Retired Director of Professional Learning |
|
Dr. Bruce Randel |
Technical Work Group (TWG) Member |
Century Analytics |
bruce.randel@centuryanalytics.com 303-842-9607
|
References
Apthorp, H., Randel, B., Cherasaro, T., Clark, T., McKeown, M.& Beck, I. L. (2012). Effects of a supplemental vocabulary program on word knowledge and passage comprehension. Journal of Research on Educational Effectiveness, 5, 160–188.
Bloom, H. S., Bos, J. M. & Lee, S.W. (1999). Using cluster random assignment to measure program impacts: Statistical implications for the evaluation of education programs. Evaluation Review, 23(4), 445–489.
Bloom, H. S., Richburg-Hayes, L.& Black, A. R. (2007). Using covariates to improve precision for studies that randomize schools to evaluate educational interventions. Educational Evaluation and Policy Analysis, 29(1), 30–59.
Constantine, J., Player D., Silva, T., Hallgren, K., Grider, M. & Deke, J. (2009). An Evaluation of Teachers Trained Through Different Routes to Certification, Final Report (NCEE 2009-4043). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
Dillman, D. A., (2000). Mail and internet surveys: The tailored design method (2nd ed.). New York: Wiley.
Drummond, K., Chinen, M., Duncan, T.G., Miller, H.R., Fryer, L., Zmach, C. & Culp, K. (2011).Impact of the Thinking Reader® software program on grade 6 reading vocabulary, comprehension, strategies, and motivation (NCEE 2010-4035). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
Glazerman, S., Isenberg, E., Dolfin, S., Bleeker, M., Johnson, A., Grider, M. & Jacobus, M. (2010). Impacts of Comprehensive Teacher Induction: Final Results From a Randomized Controlled Study (NCEE 2010-4027). Washington, DC: National Center for Education.
Hedges, L. V. & Hedberg, E. C. (2007). Intraclass correlation values for planning group-randomized trials in education. Educational Evaluation and Policy Analysis, 29, 60–87.
Hitchcock, J., Dimino, J., Kurki, A., Wilkins, C., &Gersten, R. (2011). The impact of collaborative strategic reading on the reading comprehension of grade 5 students in linguistically diverse schools (NCEE 2011-4001). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
Lipsey, M.W., Puzio, K., Yun, C., Hebert, M.A., Steinka-Fry, K., Cole, M.W., Roberts, M., Anthony, K.S., Busick, M.D. (2012). Translating the statistical representation of the effects of education interventions into more readily interpretable forms. (NCSER 2013-3000). Washington, DC: National Center for Special Education Research, Institute of Education Sciences, U.S. Department of Education.
Northwest Evaluation Association. (2005). RIT scale norms for use with achievement level tests and measures of academic progress. Lake Oswego, OR: Author.
Northwest Evaluation Association. (2009). Technical manual for Measures of Academic Progress™ and Measures of Academic Progress for primary grades™. Lake Oswego, OR: Author.
Office of Management and Budget (2006). Guidance on agency survey and statistical information collections. Washington, DC: Author. Retrieved July 18, 2012 from: http://www.whitehouse.gov/sites/default/files/omb/inforeg/pmc_survey_guidance_2006.pdf.
Schochet, P. Z. (2008). Statistical power for random assignment evaluations of education programs. Journal of Educational and Behavioral Statistics, 33, 62–87.
Spybrook, J., Bloom, H., Congdon, R., Hill, C., Martinez, A.& Raudenbush, S. (2011). Optimal design plus empirical evidence: Documentation for the “optimal design” software.
Wijekumar, K., Hitchcock, J., Turner, H., Lei, P. W., & Peck, K. (2009). A multisite cluster randomized trial of the effects of CompassLearning Odyssey® math on the math achievement of selected grade 4 students in the Mid-Atlantic Region (NCEE 2009-4068). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
What Works Clearinghouse, (2011). Procedures and standards handbook, Version 2.1. Washington, DC: Institute of Education Sciences, U.S. Department of Education.
Yoon, K. S., Duncan, T., Lee, S. W.-Y., Scarloss, B., & Shapley, K. (2007). Reviewing the evidence on how teacher professional development affects student achievement (Issues & Answers Report, REL 2007–No. 033). Washington, DC: U.S. Department of Education, Institute of Education Sciences, National Center for Education Evaluation and Regional Assistance, Regional Educational Laboratory Southwest. Retrieved from http://ies.ed.gov/ncee/edlabs .
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Subject | Section B |
| Author | Trudy Cherasaro |
| File Modified | 0000-00-00 |
| File Created | 2021-01-28 |
© 2026 OMB.report | Privacy Policy