Annex J - Formulas for Estimating Means and Variances
Annex J_Formulas for estimating means and variances.docx
Rural Community Wealth and Health Care Provision Survey
Annex J - Formulas for Estimating Means and Variances
OMB: 0536-0072
FORMULAS FOR ESTIMATING MEANS AND VARIANCES
Formulas for estimating means and variances
Exact formulas for variances using our sampling strategy are not available, since we are using a systematic random sampling procedure (with a random start) in the first stage.1 As noted in the text, the estimated variance based on a simple random sample provides a conservative estimate for the variance with systematic sampling, so we use the formulas associated with (stratified) simple random sampling in the first stage. The formulas below were derived for our case of a two stage simple random sample without replacement, with stratification in both stages (i.e., stratification of regions in the first stage and stratification of respondent groups in the second stage), and are consistent with the approach and formulas found in Särndal, et al. (2003), chapter 4.2
For a population of K potential respondents in our sample universe, a consistent and asymptotically unbiased estimate of the population mean of response variable y is given by:
1)
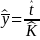 ,
,
where
 is
the estimate of the population total of y and
is
the estimate of the population total of y and
 is
the estimate of K. These estimates are determined by the
following formulas:
is
the estimate of K. These estimates are determined by the
following formulas:
2)
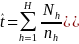
3)
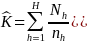 ,
,
where
h is the first stage stratum number, H is the total
number of first stage strata (= 6 for the full population), Nh
is the total number of towns in stratum h, nh
is the number of sample towns in stratum h, Mig
is the total number of potential respondents of type g in town
i, and
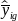 is
the sample mean of y for respondent group g in town i
(
is
the sample mean of y for respondent group g in town i
(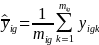 ,
where mig is the number of sample
respondents of type g in town i and yigk
is the value of y for respondent k of type g in
town i).
,
where mig is the number of sample
respondents of type g in town i and yigk
is the value of y for respondent k of type g in
town i).
A
consistent and asymptotically unbiased estimator of the variance of
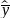 is
is
4)
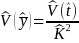 ,
,
where
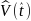 is
given by
is
given by
5)
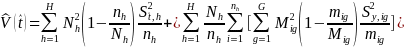
and where
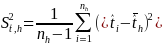 ,
,
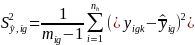 ,
,
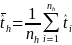 ,
and
,
and
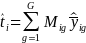 .
.
Equations 1) to 5) can also be used to estimate the mean and variance of y for subpopulations of the respondent universe. For example, to estimate the mean and variance for a subset of the first stage strata (h), the sums in these equations will be over the selected strata, rather than all six strata. Similarly, to estimate the mean and variance for a subset of the respondent groups (g), the sums will be over the selected groups rather than all G groups. We use this fact to estimate the means and variances for subpopulations discussed in the text, including communities with vs. without a hospital and communities in different regions.
1 See Särndal, et al. (2003), section 3.4.4 for an explanation of this point.
2 Our exact case is not shown in Särndal, et al. (2003), so the formulas were derived using the same approach.
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | %USERNAME% |
| File Modified | 0000-00-00 |
| File Created | 2021-01-28 |
© 2026 OMB.report | Privacy Policy