Supplemental Supporting Statement B
Revised OMB Part B Revision for FY15 Q3 Survey cuts 3-20-15 v2.docx
DOL Generic Solution for Customer Satisfaction Surveys and Conference Evaluations
Supplemental Supporting Statement B
OMB: 1225-0059
SURVEYS AND EVALUATIONS EMPLOYING STATISTICAL METHODS
B.1. Describe (including a numerical estimate) the potential respondent universe and any sampling or
other respondent selection methods to be used. Data on the number of entities (e.g., establishments, State and
local government units, households, or persons) in the universe covered by the collection and in the
corresponding sample are to be provided in tabular form for the universe as a whole and for each of the
strata in the proposed sample. Indicate expected response rates for the collection as a whole. If the collection
had been conducted previously, include the actual response rate achieved during the last collection.
The goal of this study is to evaluate EBSA’s Participant Assistance Program (PAP) and the universe consists of participant inquiries (individuals who had contacted EBSA for assistance) handled by the following 13 offices: Atlanta, Boston, Chicago, Cincinnati, Dallas, Kansas City, Los Angeles, Miami, New York, Philadelphia, San Francisco, Seattle and Washington DC.
Every two weeks, EBSA will send data on all of the participant inquiries identified as newly “closed” during the previous two weeks. The newly closed cases consist of all inquiries with a determination or closure analysis status in the Technical Assistance Information System (TAIS). Closure types include Benefit Claim- Assistance, Benefit Claim-Valid Recovery, Benefit Claim-Not Valid, Benefit Claim-Enforcement Lead, Benefit Claim-Secondary Enforcement Lead, or Benefit Claim – Referral as Abandoned Plan. Gallup will select samples of participant inquiry records on a bi-weekly basis using a simple stratified sample design. Based on information from the past administration of this study conducted by Gallup for fiscal year 2014, we anticipate an average response rate of around 30.0% for each two-week period across all offices. However, it differs across offices ranging from 20.7% for New York to 34.7% for the Seattle office. In order to examine the issue of non-response bias, a non-response bias analysis will be conducted. The non-response bias analysis plan is described in Section B3.
For the purpose of sampling, the universe of all inquiries will be first stratified by the 13 offices listed above. Each of those offices will be further sub-stratified by BA (Benefit Advisor) level inquiries. To achieve reporting at the BA level for each full-time experienced BA (defined as having been taking calls for at least the full prior quarter and closed at least 100 cases each quarter), at least during the mid-year and year-end reporting cycles, a minimum of 30 completed interviews for the reporting period (so a minimum of 60 per year per BA) is planned. Based on EBSA FY14 reports, there were approximately 118 BAs meeting the criteria for full time. Sampling, as noted above, will be done once for each two-week data collection period. In total for FY2015, there will be 24 two-week data collection periods and each quarter will consist of six such periods.
Table 1 below presents the volume of inquiry (universe counts) for each stratum (office) and also by sub-strata (BA level) within each office based on FY 2014 reports. Within an office, each of the sub-strata corresponds to a full time BA while the residual substratum includes the rest of the inquiries (non- full time and non BAs). It may be noted that the stratification scheme for 2015 will be based on this approach but the number of sub-strata in any particular quarter will depend on the actual number of inquiries received during the previous quarter at the office/BA level. At the beginning of a specific quarter, the determination of the sub-strata will be carried out based on the volume of inquiries received in the previous quarter.
Table 1: Number of Inquiries by Strata (Office and BA Status) FY2014
Participant Assistance Program (PAP) Office |
Total |
Full-Time BAs |
Non-Full Time BAs and Non-BAs |
Atlanta |
22,108 |
21,931 |
177 |
Boston |
16,078 |
15,034 |
1,044 |
Chicago |
13,723 |
13,065 |
658 |
Cincinnati |
22,334 |
22,326 |
8 |
Dallas |
21,741 |
21,030 |
711 |
Kansas City |
16,588 |
16,552 |
36 |
Los Angeles |
15,280 |
15,128 |
152 |
Miami |
21,239 |
20,731 |
508 |
New York |
17,313 |
16,576 |
737 |
Philadelphia |
13,852 |
12,735 |
1,117 |
San Francisco |
19,071 |
19,057 |
14 |
Seattle |
489 |
— |
— |
Washington D.C. |
9,420 |
9,303 |
117 |
— Not Available |
|
|
|
Based on a target of about 15 completed interviews for each of the approximately 118 full-time BAs in the agency, a minimum of about 7,080 interviews annually (118 *30 * twice a year) will be required across all 13 offices. In order to complete a minimum number of surveys from the residual sub-strata and also to generate a minimum number of surveys for each office, a total of 7,800 interviews is planned annually across all BAs. This approach will also guarantee a target precision level of +/-1-2% at the overall Agency level. About 15 interviews for each BA is targeted quarterly, with BAs with a proportionally higher level of closed cases having additional completed interviews. Inquiries handled by non-full time BAs or other non-BA staff (e.g. SBA and interns) will also be sampled (although at a lower sampling rate) from the residual sub-strata to ensure an accurate and full picture of the inquirer experience in each office. In general, the goal will be to draw a proportional sample across the BAs within an office and to ensure to the extent possible a minimum of 15 interviews for each full-time BA (sub-stratum).
In addition to the ongoing interviewing, with quarterly reporting, some offices will be oversampled to better identify areas for improvement in struggling offices and to provide reports for each BA in the selected offices each quarter (with 30 completed interviews each). Based on this goal and looking at the likely number of interviews which will fall out naturally for BAs across the 13 offices, it may be necessary to conduct up to an additional 850 interviews per year for a specified office. The criterion for selection of offices to be oversampled will be based on performance (satisfaction rating) at the overall office level. The actual selection of the offices will be made roughly once every two quarters (at the beginning of the year and after completion of the mid-year (two quarters). Once an office is selected for oversampling, the allocation of the oversample across sub-strata (BA level) within an office will be roughly proportional across sub-strata with the goal of achieving a minimum of 30 completed surveys per quarter for full time BAs within that office. In other words, oversampling will be done at the office level and no specific sub-stratum (BA level) will be targeted for oversampling. The additional number of surveys to be completed by oversampling is around 3,200 (an estimated average oversample size of 800 for each of the 4 offices to be oversampled). The total number of completed surveys (including regular and oversampling) across all 13 offices is therefore expected to be around 11,000 (7,800 + 3,200).
Table 2 below presents the approximate number of completed surveys by strata (office) under both regular and oversampling schemes. This is based on FY 2014 information and the number of sub-strata within each office. Four offices (Cincinnati, Los Angeles, Philadelphia and Washington DC) are currently selected for oversampling. The actual number of completes may vary depending on the total number of inquiries received for each office/BA during 2015. The total number of inquiries linked to Seattle office in FY2014 was, as shown in Table 1, quite low. It is anticipated that the number of inquiries for Seattle office will be significantly higher in 2015 and will be sufficient to generate around 500 completed surveys for this office as shown in Table 2 below.
Table 2: Expected number of completed surveys by strata (office)
Office |
Expected number of completed surveys in 2015 |
||
|
Regular Sample |
Oversample |
Total |
Atlanta |
570 |
- |
570 |
Boston |
680 |
- |
680 |
Chicago |
570 |
- |
570 |
Cincinnati |
550 |
800 |
1350 |
Dallas |
680 |
- |
680 |
Kansas City |
680 |
- |
680 |
Los Angeles |
550 |
800 |
1350 |
Miami |
570 |
- |
570 |
New York |
680 |
- |
680 |
Philadelphia |
550 |
800 |
1350 |
San Francisco |
800 |
- |
800 |
Seattle |
500 |
- |
500 |
Washington DC |
420 |
800 |
1220 |
Total |
7,800 |
3,200 |
11,000 |
The population parameter of primary interest will be the proportion of customers in specific categories. For example, the “proportion of customers in the population who are satisfied with EBSA overall” or the “proportion of customers who think EBSA always delivers on what they promise” will have to be estimated based on survey data. The corresponding sample estimates will be computed based on responses to the survey. On a satisfaction question such as : “How satisfied are you with EBSA overall?”, the proportion of satisfied customers may be estimated based on the proportion selecting one of the top two boxes on a 5-point likert scale. Customers will also be asked to indicate their level of agreement with statements like “EBSA treats me like a valued customer” or “EBSA always delivers on what they promise” on a 5-point scale. The proportion of customers who select one of the top two boxes will provide an estimate of the corresponding population proportion. The sample based estimate (p) of the parameter representing an unknown population proportion (P) can be expressed as:
p
=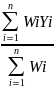 ,
,
where Yi = 1 if the ith sampled respondent belongs to the category of interest (satisfied, for example) and 0 otherwise; Wi is the sample weight attached to the ith respondent and ‘n’ is the number of completed surveys.
These parameters (proportions or means) may have to be estimated at the overall EBSA level, for each of the offices separately and possibly for other domains of interest within each stratum. For example, it may be of interest to generate similar estimates by Closure Types. The bulk of the calls (about 80 to 90% on an average) will belong to the first Closure type (those who need benefit claim assistance) and hence the number of completed surveys for this subgroup will be large enough to generate estimates of acceptable precision. Similar estimates for the other two Closure types can also be generated but the sample size within individual offices will be low and hence the estimates for these two Closure types may have to be generated at the overall EBSA level.
B.2. Describe the procedures for the collection of information including:
• Statistical methodology for stratification and sample selection – For the purpose of sampling, the universe of all inquiries will be first stratified by the 13 offices listed above. Each of those offices will be further sub-stratified by BA (Benefit Advisor) level inquiries. Sampling will be done once for each two-week data collection period. In total for FY2015, there will be 24 two-week data collection periods and each quarter will consist of six such periods. As mentioned before, inquiries handled by each full-time BA within an office will constitute one sub-stratum. All smaller BAs (not full time) within an office will be pulled together to form one combined sub-stratum. An office with 8 full time and 3 non-full time BAs will, for example, have 9 sub-strata – one for each full-time BA and an additional sub-stratum consisting of all three non-full time BAs. For any particular quarter, the determination of full-time or non-full time status for any BA will be determined based on the number of inquiries handled by that BA in the previous quarter. Sampling will be done independently within each sub-stratum (office by BA level) following a simple stratified sample design and the process will be repeated in each two-week data collection period. Within a sub-stratum, the sample size for each period will be based on the targeted number of completes and the expected response rate. In each period, the targeted number of completes will be derived by taking into account the requirement of a minimum number of 15 completes for full-time BAs and also the need for oversampling for selected offices. Once the sample sizes are determined, simple random samples of specified sizes will be drawn from the sub-strata once every two weeks.
• Estimation procedure – Sample data will be weighted to generate unbiased estimates for the target population subgroups. Within each sampling stratum (office by BA), weighting will be carried out to adjust for (i) probability of selection in the sample and (ii) non-response. Once the sampling weights are generated, weighted estimates will be produced for different unknown population parameters (means, proportions etc.) for the target population and also for population subgroups of interest. For the purpose of illustration, let us assume that we receive a total of 100 inquiries in a sub-stratum (office by BA) in a particular two-week period and we select a random sample of size 50 from those 100 inquiries. Also, assume that 15 of those 50 sampled cases actually respond i.e. we get 15 completed surveys from that sub-stratum. The weight assigned to each of those 15 completed surveys will consist of two weighting factors: (i) selection probability weight (100/50) and (ii) non-response weight (50/15). The first weighting factor is the inverse of the selection probability while the second factor is the ratio of the sample size and the number of completed surveys. The final weight will be the product of these two factors. In this specific example, the final weight assigned to each of those 15 completed cases will be (100/50) * (50/15) = 100/15. The sum of the weights of these 15 cases will add up to 100, the total number of inquiries for that two-week period for that particular sub-stratum.
Based on our previous experience in conducting this survey, we do expect some “ineligible” cases in the sample. The weighting procedure can be easily adjusted to account for ineligible cases. If, for example, 5 out of the 50 sampled cases turn out to be ineligible, the non-response weight factor will be equal to 45/15 and then the final weight assigned to each of the 15 completed surveys will be (100/50)*(45/15). The sum of the weights for all 15 cases will then equal 15*(100/50)*(45/15) = 90, the estimated number of eligible inquiries in that sub-stratum during that particular data collection period.
In
terms of mathematical symbols, the weighting steps can be described
as follows. Let
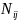 and
and
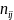 denote
the population size (total number of inquiries received) and the
corresponding sample size (number of inquiries sampled) for any
particular sub-stratum for a specific two-week data collection period
j (j=1,2,…,24). Also, let
denote
the population size (total number of inquiries received) and the
corresponding sample size (number of inquiries sampled) for any
particular sub-stratum for a specific two-week data collection period
j (j=1,2,…,24). Also, let
 denote the number of responding units in the sample in ith
sub-stratum and jth
data collection period. Then, the base-weight or the probability
weight factor (
denote the number of responding units in the sample in ith
sub-stratum and jth
data collection period. Then, the base-weight or the probability
weight factor ( )
assigned to kth
sampled unit (k=1, 2, …,
)
assigned to kth
sampled unit (k=1, 2, …,
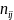 )
will be derived as:
)
will be derived as:
 =
Nij/nij…
(1)
=
Nij/nij…
(1)
At
the next step, the non-response adjustment factor (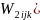 will be derived as:
will be derived as:
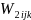 =
= … (2)
… (2)
if the kth unit (k=1, 2, …, nij) is a responding unit and 0 otherwise;
eijm = 1 if the mth unit in the sample is eligible and 0 otherwise; dijm = 1 if the mth unit is eligible and responds to the survey and 0 otherwise.
In the right hand side of equation (2) above, note that the summation in the numerator is over all sampled eligible cases whereas the summation in the denominator is over all selected eligible persons who actually respond to the survey.
The final weight (Wijl) assigned to all rij responding units (in ith sub-stratum in jth data collection period) will be the product of the two weighting factors:
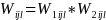 …
(3) (l = 1, 2, …,
rij).
…
(3) (l = 1, 2, …,
rij).
Construction of non-response adjustment cells based on Closure types may be considered. However, the bulk of the calls (80 to 90%) are likely to belong to the first Closure type category (those who need benefit claim assistance) only and the number of calls belonging to the other types will be small. Collapsing of non-response adjustment cells, therefore, will be necessary. We anticipate using rules based on the (i) size of the cell and (ii) value of the non-response adjustment factor. For this study, given that bulk of the calls will belong to the first category only, we anticipate using the entire stratum as the non-response adjustment cell for most strata. In some strata, it may be possible to use two cells (those who need benefit claim assistance and Others). For questions in Form 1 or Form 2 that are administered to sub-samples and hence not asked to all respondents, separate weight variables may be generated so that the sum of weights of all respondents answering those questions are projected to correct population numbers.
• Degree of accuracy needed for the purpose described in the justification – For any particular sub-stratum (office by BA), the total number of completed interviews over the 24 data collection periods will depend on the number of full-time BAs in that office. However, a minimum of about 600 surveys is expected to be completed annually within each of the 13 offices. For offices with relatively higher number of BAs and also for those undergoing oversampling, the number of completed surveys will be more then 600. For estimation of any unknown population proportion (P), for example, this will result in a margin of error of 4 percent at the 95% level of significance ignoring any design effect. The margin of error (MOE) for estimating the unknown population proportion ‘P’ at the 95% confidence level can be derived based on the following formula:
MOE
= 1.96 *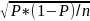 where ‘n’ is the sample size (i.e. the number of
completed surveys).
where ‘n’ is the sample size (i.e. the number of
completed surveys).
Under
the most conservative assumption (P=0.5), the MOE for a sample size
of 600 will be 1.96*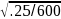 =
4.0%. After accounting for design effect, the average sampling error
is likely to be in 4% to 5% range for estimates at the individual
office level. It may be noted that, for any given office, the
allocation of sample across all 24 data collection periods is not
strictly proportional because a fixed number of completed surveys
will be targeted in each two-week period. However, for the same
office, the total number of cases (inquiries) is not expected to vary
significantly over time and hence its impact on design effect for
estimates based on data for several data collection periods should be
minimal.
=
4.0%. After accounting for design effect, the average sampling error
is likely to be in 4% to 5% range for estimates at the individual
office level. It may be noted that, for any given office, the
allocation of sample across all 24 data collection periods is not
strictly proportional because a fixed number of completed surveys
will be targeted in each two-week period. However, for the same
office, the total number of cases (inquiries) is not expected to vary
significantly over time and hence its impact on design effect for
estimates based on data for several data collection periods should be
minimal.
At
the overall agency level, the total sample size will be at least
7,800 and hence the MOE is expected to be around 1.96* =
1.1% under the assumption of no design effect. However, at the agency
level, the disproportional sample allocation across different strata
will contribute to the design effect. The
design effect was defined formally by Kish (1965) , Section 8.2, p.
258) as “the ratio of the actual variance of a sample to the
variance of a simple random sample of the same number of elements.”
Based
on Kish’s approximate formula
=
1.1% under the assumption of no design effect. However, at the agency
level, the disproportional sample allocation across different strata
will contribute to the design effect. The
design effect was defined formally by Kish (1965) , Section 8.2, p.
258) as “the ratio of the actual variance of a sample to the
variance of a simple random sample of the same number of elements.”
Based
on Kish’s approximate formula
{design effect= (sample size)*(sum of squared weights)/ (square of the sum of weights)},
the design effect at the overall agency level based on past data is not expected to exceed 2.5. After accounting for design effect, the margin of error for estimates of population proportions at the overall agency level based on a sample size of 7,800 will be about 1.7%.
The formulas for two-sample proportion test are:
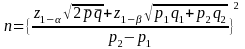 [1-tailed test]
[1-tailed test]
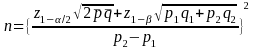 [2-tailed test]
[2-tailed test]
In these expressions,
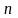 is
the sample size required to achieve the desired statistical power;
is
the sample size required to achieve the desired statistical power;
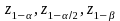 are
the normal abscissas that correspond to the respective probabilities;
are
the normal abscissas that correspond to the respective probabilities;
 are
the null and alternative hypothesis in the one-sample test;
are
the null and alternative hypothesis in the one-sample test;
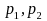 are
the two proportions in the two-sample test;
are
the two proportions in the two-sample test;
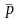 is
the simple average of
is
the simple average of
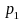 and
and
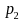 and
and
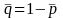 .
.
For comparison between two offices, for example, a difference of 8% in proportions (minimal detectable effect) can be detected based on this sample size with α=0.05 and 80 percent power ignoring design effect when the proportion is about 50% in one quarter and 42 percent, for example, in another. Based on the assumption of a design effect of 1.25, a difference of 9% in proportions (minimal detectable effect) can be detected based on this sample size with α=0.05 and 80 percent power ignoring design effect when the proportion is about 50% in one quarter and 41 percent, for example, in another.
• Unusual problems requiring specialized sampling procedures and – We don’t foresee any unusual problems requiring specialized sampling procedures.
• Any use of periodic (less frequently than annual) data collection cycles to reduce burden – For this study, Gallup will sample once every two weeks and the data collection for every bi-weekly sample will be completed within the following two weeks. The data collection will therefore be a continuous process throughout the year but every respondent will be contacted/interviewed within two weeks after his/her inquiry is closed. This will be done to minimize the recall error and thereby increase the overall accuracy of the survey data.
B.3. Describe methods to maximize response rates and to deal with issues of non‑response. The accuracy and reliability of information collected must be shown to be adequate for intended uses. For collections based on sampling, a special justification must be provided for any collection that will not yield "reliable" data that can be generalized to the universe studied.
Methods to maximize response rates – In order to maximize response rates, Gallup will utilize a comprehensive plan that focuses on (1) a call design that will ensure call attempts are made at different times of day and different days of the week to maximize contact rates, (2) conducting an extensive interviewer briefing prior to the field period that educates them about the content of the survey as well as how to handle reluctance and refusals, (3) having strong supervision that will ensure that high quality data are collected throughout the field period, and (4) utilizing troubleshooting teams to attack specific data collection problems that may occur during the field period. Gallup will use a 5+5 call design i.e. a maximum of five calls will be made on the phone number to reach the specific person that we are attempting to contact and another up to five calls will be made to complete the interview with that selected person.
Issues of Non-Response: Survey based estimates for this study will be weighted to minimize any potential bias including any bias that may be associated with unit level non-response. The bi-weekly files (sampling frames) to be received from DOL will contain some useful information (like Closure types) for all cases including the non-respondents. Non-response adjustment cells, if found necessary, will be formed based on these variable and then ratio type adjustments will be carried out to correct for non-response. This will make the non-response weighting procedure quite effective in terms of minimizing non-response bias, if any. The data collection mode for this study is telephone and so the item non-response rate is expected to be less compared to data collected using self-administered modes. The respondent will however have the opportunity to refuse to answer a specific question. The item missing rate is not expected to be significant and so imputation of missing item level data was not used in the past and is not recommended for the 2015 study.
As described above in Section B2, the sampling error associated with estimates of proportions at the individual office level is expected to be in the 4% to 5% range and that for the overall agency level is likely to be around 1.5% at the 95% level of confidence. For any other subgroup of interest (based on closure types, for example) the sampling error will depend on the sample size. Also, all estimates will be weighted to reduce bias. It will be possible to calculate the sampling error associated with any subgroup estimate in order to ensure that the accuracy and reliability is adequate for intended uses of any such estimate
Non-response Bias Analysis: A non-response bias analysis will be conducted to identify potential source of non-response bias. Non-response bias associated with estimates consists of two factors - the amount of nonresponse and the difference in the estimate between the groups of respondents and non-respondents. The bias of an estimate can be expressed mathematically as follows:
Bias (yr) = (1 – r) {E (yr – yn )}
where yr is the estimated characteristic based on survey respondents only, ‘r’ is the response rate and so (1 – r) is the nonresponse rate, yn is the estimated characteristic based on the non-respondents only, and E is the expectation for averaging over all possible samples.
Bias may therefore be caused by lower response rate and/or by significant difference in estimates between respondents and non-respondents. As described earlier in this section (B3), necessary steps will be taken to maximize response rates and thereby minimize any non-response bias that may be caused by low response rates. Also, non-response weighting adjustments (refer to “Issues of non-response” above) will be carried out to minimize potential non-response bias. However, despite all these attempts, non-response bias can still persist in estimates. The goal of the non-response bias analysis will be to identify potential sources of nonresponse bias on estimates and to identify potentially biased estimates.
The non-response bias analysis will compare the “Early” respondents to “Late” respondents on selected key variables of primary interest. The basic assumption in such an approach is that later respondents to a survey are more similar to non-respondents than are earlier respondents. In this study, data collection will be conducted using telephone and a respondent can receive anywhere between 1 and 10 calls to complete an interview. Respondents will be divided into two groups (Early and Late respondents) based on the number of calls received. The exact definition of these two groups will be finalized after examining the distribution of the ‘number of calls’ needed to complete an interview for this study. Comparison of estimates (proportions or means of selected key variables like proportion of satisfied customers, for example) between these two groups will be carried out by testing the hypothesis of equality of proportions (or means). This process will help identify estimates that may be subject to non-response bias.
The key variables (or survey questions) for the comparison of “Early” and “Late” respondents will include the following ten questions that are expected to be strong predictors of overall customer satisfaction. (Each of these eight questions uses a five-point scale, where 5 means strongly agree and 1 means strongly disagree and the respondent is asked to tell how much he or she agrees or disagrees with each statement as it applies to EBSA).
EBSA treats me like a valued customer
EBSA is willing to work with me to make sure my needs are met
EBSA acts in a timely fashion
EBSA does what it says it will do
EBSA is easy to reach
The information I receive from EBSA is clear and easy to understand
EBSA does its best to help me out
EBSA thoroughly answers all of my questions
EBSA is proactive in addressing my question or issue
If you had a need to work with EBSA again in the future, you would want to interact with this same benefits advisor
For each of these selected variables, the mean of the two groups (‘early’ and ’late’ respondents) will be compared based on a t- test using software SUDAAN so that the sample design and the resulting sample weights can be taken into consideration.
Let the mean (or equivalently the proportion of 1s for a 0-1 variable) of ‘early’ and ‘late’ respondents for a specific variable (Y) based on survey data be denoted by p1 and p2 respectively. Then, p1 can be written as
p1 = ∑Wiyi/∑Wi, where yi is 1 if the value of variable Y for the ith respondent is 1 and ‘0’ otherwise; Wi is the weight assigned to the ith respondent and the summation in both numerator and denominator is over all ‘early’ respondents in the sample. p2 can be similarly defined. The t-statistic for testing the equality of means for those two groups (Ho: P1=P2 vs. H1:P1 ≠ P2 where P1 and P2 are the corresponding population means) will be computed as:
t=(p1 – p2)/SE (p1 – p2) , where SE (p1 – p2) is the standard error or the estimated square-root of the variance of (p1 – p2).
In order to obtain the value of t-statistic (and the corresponding significance level or p-value), the main SUDAAN commands using the DESCRIPT procedure will be as follows:
PROC DESCRIPT DATA=XXXX FILETYPE=SAS DESIGN=STRWR;
nest strata;
WEIGHT FINALWT;
class early_late;
var Y;
contrast early_late = (1 -1)/name = "early vs. late";
print nsum t_mean p_mean mean;
The variable strata (obtained by crossing the levels of regional offices, data collection periods and BAs) will represent all the strata. The WEIGHT statement specifies the final weight variable. The CLASS statement defines the independent variables as categorical and REFLEVEL specifies the reference level for each of these variables. The early_late variable will contain two distinct values (0-1 for example) to identify the two groups (‘early’ or ‘late’) for each case in the data set. The VAR statement will include the variables for which the mean has to be compared between the two groups. For each selected variable included in the VAR statement, the hypothesis of equality of means will be rejected (or not) based on the p-value (less than 0.05 or not).
Non-response bias analysis may also involve comparison of survey based estimates to known Population Values that may be available. For this study, variables like Subject entry code, Closure types and Days_to_close (of inquiry) will be available for all cases on the sampling frame. It is, therefore, possible to compute the actual value of population parameters that are functions of these variables and compare those with the corresponding sample based (weighted) estimates. For example, the following three population parameters may be used for this comparison.
P_BCA: Proportion of Benefit Claim Assistance (BCA) calls (derived from the Closure Analysis variable on the sampling frame)
M_Close: Mean of the variable Days to Close (derived from Days_to_close variable on the sampling frame)
P_PBS: Proportion of calls falling under a certain subject entry code (for example, the proportion of calls under PBS (Pension Benefits, Social Security Notice). This will be derived from the Subject Entry Code variable on the sampling frame.
The corresponding sample-based weighted estimates for the three population parameters will be generated using the values of those variables from the completed surveys. The comparison will be carried out using a one-sample t-test based on a t-statistic = (p–P)/SE(p) where ”p” is the sample-based estimate of the corresponding population proportion (or mean) ”P,” and SE(p) is the estimated standard error of p. The main SUDAAN statements to be used for the computation of SE(p) for the variable “Days to Close”, for example, will be as follows:
PROC descript data = XXXX filetype = sas design = strwr;
NEST strata;
WEIGHT finalwt;
VAR days_to_close;
PRINT nsum wsum mean semean;
[NEST statement specifies the strata determined by office, BA and period (2-week data collection period) and FINALWT is the final weight variable. The VAR statement will include the variable (M_Close: Days to Close) for which the mean was to be compared between the two groups. The hypothesis of equality of means will be rejected (or not) based on the p-value (less than 0.05 or not).]
Once SE(p) is estimated using SUDAAN, the t-statistic will be calculated using the values of p and P, and the hypothesis of equality (p = P) will be rejected (or not) based on the observed significance level (less than 0.05 or not).
B.4. Describe any tests of procedures or methods to be undertaken. – Cognitive/pilot tests for minimizing burden and improving utility were conducted in the past and the survey questionnaire for this study has now been standardized. Prior to the requested edits, item response and timing analysis was conducted to determine what items to delete from the survey and to identify what items to include in the long and short form versions of the survey.
B.5. Provide the name, affiliation (company, agency, or organization) and telephone number of individuals consulted on statistical aspects of the design and the name of the agency unit, contractor(s), grantee(s), or other person(s) who will actually collect and/or analyze the information for the agency.
The following individuals consulted on statistical aspects of the design and will also be primarily responsible for actually collecting and analyzing the data for the agency.
Name |
Agency/Company/Organization |
Number Telephone |
Susan Conner |
Gallup Organization |
202-715-3124 |
Manas Chattopadhyay |
Gallup Organization |
202-715-3179 |
Camille Lloyd |
Gallup Organization |
202-715-3188 |
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| File Modified | 0000-00-00 |
| File Created | 2021-01-29 |
© 2026 OMB.report | Privacy Policy