MPD_Part_A_031013

Impact Evaluation of Math Professional Development

OMB Clearance Request, Part A

PREPARED BY:

American Institutes for Research^®
1000 Thomas Jefferson Street, NW, Suite 200

Washington, DC 20007-3835

PREPARED FOR:

U.S. Department of Education

Institute for Education Sciences

March 12, 2013

Contents

Page

Introduction 1

Purpose 3

Research Questions 4

Intervention 4

Experimental Design 8

Data Collection 17

Supporting Statement for Paperwork Reduction Act Submission 20

References 30

List of Exhibits

Exhibit 1. Number and Distribution of Hours of Each Component of the Intervention

Exhibit 2. Number of Districts, Schools, and Teachers Expected to Participate

Exhibit 3. Estimated MDES for Teacher Knowledge, Under Different Assumptions About the Percentage of Variance Explained by Blocking and the Percentage of Variance (R²) Explained by Teacher Covariates

Exhibit 4. Estimated MDES for Classroom Practice (MQI Scores) Based on One or Two Observations, Under Different Assumptions About the Percentage of Variance (R²) Explained by Teacher Covariates

Exhibit 5. Estimated MDES for Student Achievement, Under Different Assumptions About the Percentage of Variance (R²) Explained by Covariates at Student and Teacher Levels

Exhibit 6. Respondent Universe for Recruitment Activities

Exhibit 7. Proposed Data Collection, 2013–2014

Exhibit 8. Alignment of Intel Math Content and the Teacher Knowledge Item Pool (MTEL)

Exhibit 9. Hour Burden for Respondents for Recruitment Activities

Exhibit 10. Hour Burden for Respondents for Study Data Collection

Introduction

The need to improve U.S. students’ math achievement is clear. A minority of U.S. students score at or above proficient levels in math and science on the National Assessment of Educational Progress (NAEP), and recent math and science achievement scores on the Programme for International Student Assessment consistently place U.S. 15-year-old students no higher than average internationally (National Center for Education Statistics, 2011; National Mathematics Advisory Panel; 2008; National Science Board, 2012). Teacher professional development (PD) is considered to be an important pathway to improving teaching and learning in general, and improving mathematics teaching and learning, in particular, and federal, state and local governments invest billions of dollars each year to support the development and delivery of preservice and inservice training.

Despite these investments in PD, there is limited rigorous evidence of the effectiveness of specific PD strategies. In particular, there is a lack of evidence about PD that places a strong emphasis on boosting elementary teachers’ content knowledge and transferring that knowledge to the classroom, though mathematicians and math educators have argued that gaps in elementary teachers’ math content knowledge must be addressed. Recognizing this need, the National Center for Education Evaluation (NCEE) at the Institute of Education Sciences (IES) commissioned a study to evaluate the impact of an intensive, content-focused PD program on teachers’ content knowledge, classroom practice and student achievement. This study will contribute much-needed information and evidence to a field in need of high quality information about improving students’ math performance and teacher quality in our nation’s schools.

The evaluation design for the Impact Evaluation of Math Professional Development involves the random assignment of approximately 200 grade 4 teachers in six districts to one of two conditions: Treatment teachers will be offered the study’s PD intervention, which includes 80 hours of mathematics content-focused PD and 13 hours of supports to transfer that knowledge to the classroom; control teachers will be offered their district’s business-as-usual PD. The teacher-level random assignment will be conducted within-school and within-fourth-grade to maximize the study’s statistical power to detect impacts. In cases where there is an even number of fourth-grade teachers, the treatment and control groups will be of equal size. In cases where there is an odd number of fourth-grade teachers, the treatment group will always exceed the control group by one teacher. Providing the extra treatment teacher in these cases will help offset potentially greater attrition from the treatment group (which must participate in the PD intervention), as well as increase the likelihood of having multiple treatment teachers from the same school, which is preferable from the PD vendors’ perspective.

NCEE is requesting clearance to carry out recruitment and data collection activities for the Impact Evaluation of Math Professional Development. Recruitment activities include contacting a purposive sample of districts, schools and teachers to establish their eligibility and interest in participating in the study. Data collection activities include administering three teacher knowledge assessments (baseline and two follow-ups), a teacher survey, an end-of-year student assessment, and an extant data collection protocol.

This evaluation is authorized by Title IX, Part F of the Elementary and Secondary Education Act, section 9601 as amended by the “No Child Left Behind Act of 2001” (20 USC 7941).

This package contains four major sections:

1. Description of the Impact Evaluation of Math Professional Development

   • Purpose

   • Research Questions

   • Intervention

   • Experimental Design

   • Data Collection

2. Supporting Statement for Paperwork Reduction Act Submission

   • Justification (Part A)

   • Description of Statistical Methods (Part B)

3. Appendix A – Recruitment Materials

   • A-1 IES Letter of Support

   • A-2 District Screening Protocol

   • A-3 School Screening Form

   • A-4 Teacher Interest Form

4. Appendix B – Data Collection Instruments

• B-1 Teacher End-of-Year Survey

• B-2 Extant Data Collection Protocol

Description of the Impact Evaluation of Math Professional Development

Purpose

The Impact Evaluation of Math Professional Development is designed to examine the implementation and impact of a widely-used, intensive PD program that has a strong emphasis on developing teachers’ content knowledge and supporting the transfer of knowledge into the classroom. The PD program was determined by the U.S. Department of Education to be the most promising, scalable intervention with these features. More specifically, the program being tested in this evaluation includes (1) the Intel Math Program, an 80-hour course to be delivered in summer/early fall 2013, (2) the Math Learning Community (MLC), a 10-hour follow-up component in which groups of teachers collaboratively analyze student work on topics covered in the summer Intel Math course, and (3) a 3-hour video feedback component, in which teachers receive feedback regarding the quality and clarity of their mathematical explanations from video lesson excerpts on topics emphasized in Intel Math and the MLCs. All of these activities will be delivered by trained Intel course instructors and MLC facilitators beginning in summer 2013. By testing an intervention that incorporates features the available research suggests are essential, this study has high policy value and relevance to the field.

To determine the impact of the PD program on teacher knowledge, teacher practice and student achievement, a purposive sample of six districts and approximately 200 4th grade teachers will be recruited to participate in the study in 2013-14. These districts will be selected according to multiple criteria, including size, structure of math instruction, student composition of math classes, content of math instruction, and prevalence of competing curricular or PD initiatives occurring during the 2013-14 school year.

Recruitment in eligible districts will focus primarily on identifying teachers in 4th grade who are willing to participate in the study and who have the support of their principals to do so. The study focus is on upper elementary teachers because they are less likely to have a strong math background than middle school teachers. The particular focus on one grade level for the evaluation is for the sake of clarity, simplicity, and to control study costs. Fourth grade was chosen over 5^th grade because it falls right at the center of the K-8 spectrum covered in the Intel Math course and the Intel topics are more closely aligned with topics typically covered in 4th grade than those in 5th grade.

Within each school, the volunteer 4th grade teachers will be randomly assigned to either the treatment or the control group. Teachers in the treatment group will receive the study’s PD intervention from summer 2013 through spring 2014. Control group teachers will participate in their districts’ and schools’ business-as-usual PD during that time. During the one-year implementation period, data will be collected to support analyses of the implementation and impact of the PD program, with final data collection of teacher and student outcomes in spring 2014 and all analyses and reporting completed by winter 2016.

Research Questions

The study is designed to answer two main research questions, the first focusing on the impact of the PD program on teacher and student outcomes and the second focusing on program implementation.

RQ1. What is the average impact on teachers’ content knowledge, teachers’ classroom practices, and student achievement, of offering a specialized PD intervention relative to “business as usual” PD?

RQ2. How is the PD intervention implemented? What challenges were encountered during the process of implementing the intervention?

The study’s main outcome measures are teachers’ content knowledge, classroom practices, and student achievement. We will measure teachers’ content knowledge at three timepoints: first, at baseline (summer 2013), second after completion of the content-intensive summer PD component (fall 2013), and third at the end of the school year (June 2014). Content knowledge will be measured with a mathematics assessment composed of items in the Massachusetts Test for Educator Licensure (MTEL) for elementary math teachers. We will measure teachers’ classroom practice in spring 2014 using the Mathematical Quality of Instruction (MQI) instrument, which is a previously-validated observation protocol applied to video-recorded observations of teachers’ lessons. Finally, we will measure student achievement at the end of the 2013-14 school year with two instruments: (1) the state math assessment (standardized across states) at baseline (spring 2013) and follow-up (spring 2014), and (2) a study-administered assessment in a random sample of 10 students per participating teacher (total N = 2,000).

In addition, the study team will administer a survey in June 2014 to collect teacher background characteristics for use as covariates in the impact analyses for RQ1 and information about implementation and PD service contrast for RQ2. (See Data Collection section for a description of the study measures and data collection plans and Supporting Statement section A.12 for the associated estimates of burden for those instruments that carry burden.)

Intervention

The existing literature suggests that any high-quality PD program should have: (1) a heavy emphasis on comprehensively developing mathematical content knowledge and (2) a well-defined teacher support structure to ensure that the training is transferred into the classroom. Therefore, IES is interested in testing a PD program that has an intensive and comprehensive mathematical content component (i.e., an intensive summer institute for math teachers ) and supports teacher efforts to incorporate such learning into their everyday teaching (e.g., structured professional learning communities that reinforce the implementation of PD practices). The math content in PD programs is typically taught using one of two general approaches. The first approach is more similar to a traditional university mathematics course, where the focus is directly on teaching teachers the pure math content underlying the topics to be taught in the classroom and on enabling teachers to actually practice doing the mathematics. The second approach typically involves the use of analysis of actual student work and classroom case scenarios to indirectly strengthen teacher participants’ own understanding of the underlying math content. Given that prior studies such as Garet et al (2011) have primarily tested PD programs employing the second approach, IES is instead interested in testing a PD program employing a more explicit approach to teaching math content. IES is also interested in testing a PD program that is presently policy relevant, meaning that the PD is currently being implemented across multiple districts and states, and could be similarly implemented consistently in a large-scale evaluation or by other sites if desired. Practically, this implies that the PD is an “off-the-shelf” program that requires no customization and possesses the infrastructure for scale-up across multiple states.

After examining several existing math PD programs (including Developing Mathematical Ideas, Lesson Study with Fractions Toolkit, and Math Solutions), IES identified the Intel Math Program in combination with a Mathematics Learning Community (MLC) as a comprehensive and intensive set of PD activities that meet the requirements described above. Since its inception in 2006, over $5 million has been invested in Intel Math while being implemented in at least seven states and featured in federally-funded Math Science Partnership grants for Arizona and Massachusetts, as well as in Massachusetts’ Race to the Top agenda. Although a few exploratory studies have been conducted, there is no rigorous evidence of the impacts for this type of program on teacher and student outcomes, despite its growing popularity.

Thus, the intervention being tested in this study is designed to support teachers’ development of math content knowledge and the transfer of that knowledge to students. The intervention has three components, the core of which is the Intel Math Program. Intel Math is an 80-hour, university course-like program that focuses on strengthening teachers’ mathematics content knowledge; it will be delivered primarily in summer 2013. The PD intervention continues into the 2013-14 school year with a support structure designed for use with Intel Math, the Mathematics Learning Community (MLC). The MLC will provide 10-hours of follow-up, collaborative meetings (five, two-hour meetings) that focus on analyzing student work on topics addressed in Intel Math. The MLC facilitators will also deliver direct feedback to participating teachers on their classroom practice (video recorded three times during the school year) with a focus on the quality and clarity of the teachers’ mathematical explanations on topics addressed in Intel Math and the MLC meetings. Teachers will spend three hours across the three video feedback cycles, bringing the total of the three-part intervention to 93 hours.

The focus of the evaluation is on the effects of the intervention on 4th grade teachers and their students. However, teachers of other grade levels will be invited to participate in parts of the intervention, as described in the following sections.

Intel Math

Intel Math is a widely used PD program. The program is currently being implemented in 11 states and 49 cohorts of teachers – more than 1,000 K-8 teachers in total. The program has a strong focus on improving teachers’ math content knowledge (Mundry et al., 2011). About 90 percent of the focus is on foundational math content for K–8 teachers; the other 10 percent is on pedagogy. Teachers learn the content primarily by solving conceptual and computational math problems grounded in real-world settings, and receive feedback from their instructors (each course is co-taught by a university mathematician and mathematics educator). Teachers are encouraged to use and share multiple solution methods, and the course emphasizes helping teachers see how arithmetic and algebra are interconnected and represent the same mathematical ideas. The 10 percent of the course that is devoted to pedagogy examines strategies associated with teaching the content in each unit, mostly through the examination of student work samples.

The topics of the Intel Math course are as follows:

• Unit 1: addition

• Unit 2: subtraction

• Unit 3: multiplication

• Unit 4: division

• Unit 5: operations with fractions

• Unit 6: rational numbers

• Unit 7: linear relations

• Unit 8: functions

Among the eight units in the course, Units 1–5 focus directly on topics included in the Grade 4 Common Core State Standards in Mathematics (CCSSM) (addition, subtraction, multiplication, division, and meaning of fractions). Units 6–8 focus on ratio/proportion, algebra, and linear functions, which are topics important for 4th grade teachers to know so that they can provide instruction that appropriately lays the foundation for students’ learning in future grades. Intel Math is delivered face-to-face, rather than remotely, because of the emphasis on problem-solving, solution-sharing and cooperative learning.

The course is typically taught to teachers of multiple grade levels, which allows for discussions about how concepts develop over time and opportunities for teachers to deepen their understanding of the math that come before and after the math that they teach. In typical implementation of Intel, schools are also encouraged to ensure that at least two teachers participate together; this gives teachers partners for transportation and greater opportunity to continuing discussing course content.

In order to implement Intel Math in the typical manner for the study, a mix of teachers in grades K-8 will be invited to participate along with the 4th grade study teachers. We will recruit approximately 10 additional teachers—five teachers from grades K-3 and five from grades 5-8 to provide a balance of teachers in grades below and above the targeted grade 4. The teachers in other grade levels will be selected in an effort to ensure that all or most of the 4th grade study teachers who are randomized to the treatment group have another teacher from their school participating in the PD intervention.

The study’s main focus is on improving teachers’ content knowledge, and the Intel Math program is the core of the study’s PD intervention. The other two components, described next, are intended to support the enactment of teachers’ content knowledge in their classroom practice.

Mathematics Learning Community (MLC)

The MLC offers a support structure to help teachers transfer the content they are learning through Intel Math to their students’ work. The centerpiece of each two-hour session is the analysis of student work samples using a standardized protocol. Looking at student work encourages teachers to think about the underlying math concepts in problems with which students struggle, by analyzing different student approaches, solutions, common errors, and misconceptions. According to the MLC developers, the learning communities function best when they are implemented primarily in the fall, which is relatively close to when teachers studied the same topics in the Intel summer course; strongly supported by district and school leadership; and integrated into the district’s instructional system—curriculum, pacing guides, curriculum, assessments—as opposed to being an add-on to the full set of instructional and assessment demands facing teachers on a regular basis. They are typically but not always implemented with teachers from multiple grade levels; for example, teachers in the 3-5 grade band.

The complete MLC program includes 15 sessions that are typically implemented over two years and focus on topics spanning grades K-8. However, with the study’s focus on 4th-grade teachers and duration of one year, we have selected 5 MLC sessions that are most aligned to grade 4 topics and Units 1–6 of the Intel course, maximizing the coherence of the PD intervention within the instructional context of each district.

The participants in the MLCs will include all of the 4th grade study teachers and those teachers in grades 3 and 5 who participated in the Intel course. This will ensure that the configuration of the MLCs for the study is similar to that in typical implementations of the program, where including a mix of teachers from the 3-5 grade band is viewed as desirable. As noted, high priority for selection will be given to 3^rd and 5^th grade teachers in schools where only one 4th grade study teacher will be randomized to the treatment group (because, e.g. there are only two volunteer 4th grade teachers in the school).

Video Feedback

The third component of the intervention includes three video feedback cycles that are designed to help teachers improve the quality, clarity and coherence of their explanations of topics that are central to grade 4, as defined by Intel Math, and as the topics appear in each district’s pacing guide (multiplication, division and fraction concepts). To plan each cycle, the MLC facilitator will work with each teacher to select an appropriate lesson to be videotaped, support the teacher in video recording the lesson, and send the video to be scored by trained coders at Harvard University. The Harvard coders will score each lesson using the MQI, which rates the quality and clarity of the mathematical explanations and discourse in the lesson. The MLC facilitator will then use the MQI scores and illustrative clips provided by the Harvard coders to prepare feedback for the teachers. The feedback will be discussed in one-hour, one-on-one meetings with the teachers; the meeting time will include making a plan for improving the quality of explanations on these topics as they are revisited in future lessons and as they relate to other topics that will be introduced later in the year. (For example, if the focus of an initial lesson is clarifying the meaning of numerator and denominator, the clarity of language and presentation of these concepts would be revisited when students add and subtract fractions later in the year).

The participants for the video feedback component are the 4th grade teachers in the study sample.

Together, the three intervention components are intended to boost teachers’ content knowledge and provide a support structure for transferring that knowledge to the classroom.

Schedule for Implementing the Intervention

Each district will have some flexibility in determining the schedule for implementing the three-part intervention which totals about 93 hours for participating teachers. The Intel Math program developers require the completion of a minimum of five consecutive days of the 13 total days during the summer, and the MLC developers have indicated that the MLC meetings function best when teachers have completed most, if not all, of Intel Math. The video feedback sessions will occur when teachers are teaching specific, key grade 4 math topics that are emphasized in Intel Math and the MLCs. Thus, the video feedback meetings will depend on the sequencing of math topics in each district, but we anticipate that the majority of video feedback sessions will occur in October, November and January of the 2013-14 school year. Exhibit 1 illustrates how the 93 hour intervention might be implemented from summer 2013 through spring 2014 if the district offers the full Intel course in the summer.

Exhibit 1. Number and Distribution of Hours of Each Component of the Intervention

PD Component	PD Focus	Number and Grade Level of Participants per District	2013		2014		Total (Hrs)
			July–Sept	Oct–Dec	Jan–Mar	Apr-June
Intel Math	Math content	~ 16 in grade 4 ~ 5 in grades K-3 ~ 5 in grades 5-8	80 hrs				80
Math Learning Community (MLC)	Student work analysis	~ 16 in grade 4 ~ 5 in grades 3 and 5		6 hrs	4 hrs		10
Video Feedback Cycles (VFCs)	Practice explanations	~ 16 in grade 4		2 hrs	1 hr		3
Total Hrs			80 hrs	8 hrs	5 hrs		93

Experimental Design

The Impact Evaluation of Math Professional Development has an experimental design with randomization of 4th grade teachers to treatment and control conditions within participating schools and districts. The study team will recruit six districts to implement the study’s PD program. The expected number of schools, districts, and teachers are shown in Exhibit 2.

Exhibit 2. Number of Districts, Schools, and Teachers Expected to Participate

Participant Type	Assumed N
Districts	6
Schools	67
Teachers	200

Within each of the six districts, the study team will identify approximately 33, 4th grade teachers who are willing to participate and have the support of their principals to do so. Assuming an average of three eligible and willing teachers per school, we assume approximately 11-12 schools will participate, for a total of approximately 67 schools.

The 200 4th grade teachers will be randomly assigned to either the treatment or the control condition within schools following baseline measurement of teacher knowledge. The projected numbers of schools and teachers are based on the study’s design, analytic strategy and associated power calculations, which are described in the following sections. In cases where there is an even number of fourth-grade teachers within a school, the treatment and control groups will be of equal size. In cases where there is an odd number of fourth-grade teachers, the treatment group will always exceed the control group by one teacher. Providing the extra treatment teacher in these cases will help offset potentially greater attrition from the treatment group (which must participate in the PD intervention), as well as increase the likelihood of having multiple treatment teachers from the same school, which is preferable as described in the prior section on the intervention. Although this may result in a slightly unbalanced experimental design, the adverse effect on statistical power to detect impacts is negligible.

The choice of defining volunteer 4th grade teachers as the unit of assignment and analysis for the evaluation is based on both theoretical and practical considerations. The study is focused on teachers who are willing and able to commit the required time and whose principals believe they would benefit from intensive, content-focused PD. This approach will provide a test of the way intensive PD might be rolled out, defining the population as teachers who are motivated to improve and have the support of their principals, so that it is viewed as an integral part of each participating teacher’s plan for development, not an idiosyncratic activity. Principal support—as well as being important for helping to promote and sustain full attendance in the PD activities—will also enable the study to avoid having only the most motivated teachers from volunteering to participate. Defining the population as all 4th grade teachers in any given school would not ensure the required teacher commitment, and defining the population as all 4th grade teachers who volunteer (ignoring schools) would not ensure the required support from the principal. Furthermore, in terms of statistical power, random assignment of teachers within schools is a more powerful design than both random assignment of teachers districtwide (rather than within school) and random assignment of schools. Therefore, the study’s design is efficient and will allow for unbiased estimates of the impact of the math PD intervention on the key outcomes of interest.

Statistical Power for Impacts on Teachers and Students

Among the most important design issues is ensuring that the sample size is adequate to provide a strong answer to RQ1, concerning the impact of PD intervention on teacher knowledge, teacher practice, and student achievement. The appropriate target minimum detectable effect sizes (MDES) for this study was considered both in terms of prior research and the expected treatment-control contrast, given the intensity of the study PD intervention. NCEE’s prior randomized study of math PD for 7^th grade teachers reported an average impact of the PD on teachers’ specialized content knowledge of 0.28 SDs (Garet et al., 2011). Bell, Wilson, Higgins, and McCoach (2010), in a randomized study of Developing Mathematical Ideas, a 48-hour summer institute that combined work on math content with work on student thinking and lesson planning and analysis, obtained an impact of 0.24 SD on the LMT and 0.57 on an open-ended test developed for the study. To further consider the appropriate MDES for teacher outcomes, one strategy is to work backward, assessing the magnitude of the impact on teacher outcomes required to translate into a detectable indirect impact on student achievement. Our review of related literature suggests that PD would need to have an impact of roughly 1 SD on teachers to translate into a policy relevant impact on student achievement. Effects of roughly this size have been obtained in several randomized studies, including Carpenter, Fennema, Peterson, Chiang, and Loef (1989), Allen et al. (2011), and Supovitz (2012). Given the prior literature, the study has established a MDES of 0.30 – 0.40 for teacher outcomes as adequate though conservative, and policy relevant.

For student achievement outcomes, the study has established a MDES of 0.12. Several recent studies of intensive PD have obtained effects of at least 0.20 SD on achievement (e.g., Allen et al. 2011), implying that the target MDES for the study is reasonable.

We estimated the MDES for teacher and student outcomes, assuming 80 percent power and an alpha level of .05 for two-tailed significance tests. We further assumed that the study sample includes 6 school districts, 200 teachers with 2 to 4 teachers (three on average) per participating school, and balanced sample allocation.

Exhibit 3 presents the results of power analyses for teacher knowledge as the outcome. The MDES ranges from 0.20 – 0.27 depending on the percent of variance assumed to be removed through blocking teachers within schools for random assignment, and the percent of variance in the outcome explained by teacher covariates. The covariates for analyses of the intervention’s impact on teacher knowledge include background characteristics and the pretest measure of teacher knowledge; these covariates are likely to explain 60-70% of the variance in the knowledge outcome.

Exhibit 3. Estimated MDES for Teacher Knowledge, Under Different Assumptions About the Percentage of Variance Explained by Blocking and the Percentage of Variance (R²) Explained by Teacher Covariates

Percent of Variance Explained by Blocking	Teacher-Level R2 = 50%	Teacher-Level R2 = 60%	Teacher-Level R2 = 70%
10%	0.27	0.24	0.21
15%	0.26	0.23	0.20

Power analyses for MQI measures of classroom practice (richness of math, precision, response to student errors, student participation in meaning making) based on video observations depend on the number of teachers observed and the number of lessons video recorded for each teacher (Raudenbush & Sadoff, 2008). We assumed 88 percent of the within-district variance in lesson ratings is at the lesson level, 10 percent at the teacher level, and 2 percent at the school level.¹ For the fall measure of classroom practice, the estimated MDES with 200 teachers and one observation per teacher is 0.39. For the spring measure of classroom practice, the estimated MDES with 200 teachers and two observations per teacher is 0.28 – 0.29, assuming different percentages of outcome variance explained by teacher-level covariates, as presented in Exhibit 4. The percent of variance explained by teacher covariates for analyses of classroom practice as the outcome are anticipated to be lower than for teacher knowledge as the outcome because there will be no pre-study baseline measure of classroom practice to include in the vector of covariates.

Exhibit 4. Estimated MDES for Classroom Practice (MQI Scores) Based on One or Two Observations, Under Different Assumptions About the Percentage of Variance (R²) Explained by Teacher Covariates

Number of Lessons Observed per Teacher	Teacher-Level R2 = 10%	Teacher-Level R2 = 20%	Teacher-Level R2 = 30%
1 (fall 2013)	0.39	0.39	0.39
2 (spring 2014)	0.29	0.29	0.28

Exhibit 5 presents the estimated MDES for student achievement, based on a conservative assumption that 15 percent of the total variance in student achievement is between schools, 10 percent is between teachers within schools, and 75 percent is between students within teachers (Jacob & Zhu, 2009). The results in the table are based on a range of assumptions about the percentage of variance explained by teacher-level and student-level covariates (R² = 50 percent to 70 percent) and about the number of students per teacher (N = 10 for a study-administered achievement test and N = 20 for extant achievement data). Depending on the covariate R² at both the teacher and student levels, the estimated MDES ranges from 0.09 – 0.12 for student achievement scores on a study administered test and from 0.08 – 0.10 for achievement on state assessments (extant data). All of the estimated MDES under different assumptions fall at or below the target for student achievement outcomes of 0.12 SD.

Exhibit 5. Estimated MDES for Student Achievement, Under Different Assumptions About the Percentage of Variance (R²) Explained by Covariates at Student and Teacher Levels

Number of Students per Teacher and Student-Level R2	Teacher-Level R2 = 50%	Teacher-Level R2 = 60%	Teacher-Level R2 = 70%
N = 10, R2 = 50%	0.12	0.11	0.10
N =10, R2 = 60%	0.11	0.11	0.09
N = 10, R2 = 70%	0.11	0.10	0.09
N = 20, R2 = 50%	0.10	0.10	0.09
N = 20, R2 = 60%	0.10	0.09	0.08
N = 20, R2 = 70%	0.10	0.09	0.08

Sample and Recruitment

As noted in the Introduction, the study’s focus on 4th grade teachers for the study sample is based on recognition of the importance of improving content knowledge among upper elementary level teachers, who are less likely than secondary teachers to have focused on mathematics in their preservice training. Grade 4 is in the middle of the K-8 spectrum covered in the Intel Math course, and topics that are typically taught in 4th grade are well-aligned to the Intel curriculum.

While for these reasons the study has chosen to conduct the evaluation with a sample of 4th grade teachers and their students, as noted in the Intervention section above, typically implementation of the Intel Math course and the MLCs includes teachers from multiple grades. In order to ensure typical implementation for the study, we will also recruit an additional set of teachers in each district from these other grade levels to participate in these components of the intervention.

Specifically, we will work with each district in spring 2013 to invite teachers in grades K-3 and 5-8 to apply to participate in the Intel course to be offered in summer 2013. Of those who apply, we will select up to 10 teachers to participate, approximately half from grades K-3 and half from grades 5-8.

Teachers in grades 3 and 5 will additionally be invited to participate in the MLCs along with the 4th grade study teachers. These additional teachers will not participate in the video feedback component, however. We will not be collecting any data on the non-4th grade teachers who participate in various aspects of the PD intervention, and they are not considered part of the study sample.

The exact number of teachers per grade level will be determined for each district depending on the number of volunteer 4th grade teachers per participating school. As noted above, in typical implementation of Intel and the MLCs, schools are encouraged to ensure that at least two teachers per school participate, so that the teachers have a partner or a group with whom they can discuss the content and travel to sessions. To select the additional teachers from other grade levels to participate in Intel and the MLCs, we will give strong priority to those in schools in which there is only going to be one teacher randomized to the treatment group (e.g. where there are two volunteer 4th grade teachers). Therefore, a specific selection plan for each district will be devised after the targeted recruitment of 4th grade teachers is completed.

To identify the pool of districts from which to recruit, we will conduct the following steps. First, we will use the Common Core of Data to identify states that have at least one district with 16 or more elementary schools containing at least two grade 4 teachers. Next, we will select districts on the basis of eligibility in terms of size, structure and content of math instruction, and stability and certainty in planned initiatives, as well as interest in participating in the study and willingness to engage school staff in recruitment and study activities. Selection criteria that we will use to screen districts specifically include:

• Size: Districts must have 16 or more elementary schools with at least two 4th grade teachers per school who may be interested in volunteering to participate in the study;

• Structure of math instruction – non-departmentalized and not ability tracked: Districts must have schools in which (a) teachers are non-departmentalized but rather they teach all or most subjects including math, and (b) students are not sorted by ability level into classes;

• Content of math instruction – no major changes: Districts must indicate that the curricula they plan to implement in 2013-14 is not a major change or overhaul from the prior year;

• Other PD activities or initiatives: Districts must indicate that they do not plan to (a) provide 4th grade math teachers PD similar in focus or intensity to what will be provided by the study during the school year 2013-2014 or (b) initiate a district-wide initiative that might interfere with grade 4 teachers willingness to participate or ability to benefit from the PD provided by the study.

To select schools within districts for the study, we will seek participation from schools in which (1) the principal supports the purpose and design of the study, (2) at least two eligible 4th grade teachers express a willingness to participate, (3) math instruction is not departmentalized, and (4) students are not tracked by ability into separate 4th grade classes.

We will work with district and school staff to share materials and information about the study with 4th grade teachers, and to arrange meetings to discuss study details, answer their questions, gauge their interest, and seek documentation of their commitment to participate. The recruitment strategy thus will create a sample of teachers who are willing and able to commit the required time and whose principals believe they would benefit from intensive, content-focused PD. This approach will provide a test of the way intensive PD might be rolled out in practice, defining the population as teachers who are motivated to improve and have the support of their principals so that it is viewed as an integral part of each participating teacher’s plan for development, rather than an idiosyncratic activity. Assuming an average of three 4th grade teachers per school who are eligible and willing to participate, we anticipate recruiting 11-12 elementary schools per eligible school district (total of 67 schools) to achieve our target sample size of 200 teachers.

As noted previously, about half of the teachers will be randomly assigned within schools to participate in the PD intervention, and the remaining will experience the “business as usual” mix of PD opportunities offered to control teachers between July 2013 and June 2014. We expect these opportunities to include some content-focused training (e.g., training related to CCSSM implementation), which are likely to total no more 1–2 days (8–16 hours) in any given district.

We intend to maximize the treatment contrast while ensuring the study represents a real-world test of the study’s PD intervention. During recruitment, we will learn as much as possible about the PD opportunities that are planned for 2013–14 in potential district sites, and we will screen out those school districts that are planning to implement math PD that has a similar intensity/duration and strong emphasis on content knowledge and transferring that knowledge to the classroom as the PD intervention being tested.

Part B.1 (Respondent Universe and Sampling Methods) of this package describes the procedures used for recruitment, materials used for recruitment and the recruitment screening protocols, because they involve burden by prospective participants.

Exhibit 6 shows the respondent universe for proposed recruitment activities to be conducted to gauge the interest of potential study participants, and to obtain the target sample of 200 4th grade teachers in six districts.

Exhibit 6. Respondent Universe for Recruitment Activities

Data Source	Number of Records
District Screening Protocol	68
School Screening Protocol	114
Teacher Interest Form	340

Analytic Strategy for Analyses of Program Impacts

RQ1 assesses the impact of the PD intervention on teacher and student outcomes. Our analytic strategy for both sets of outcomes are described next.

Intent-to-Treat Impact Analyses. The main analyses testing the effects of the PD intervention on teacher and student outcomes (RQ1) take an intent-to-treat (ITT) approach, meaning that all teachers who were randomly assigned to the treatment and control groups are included in the analysis sample. Teacher knowledge will be based on the following regression model:

Y_jk = + + + r_jk (1)

where Y_jk is a measure of teacher knowledge for teacher j in school k, SCHOOL_s is a set of indicators for the S study schools, PD_jk is an indicator for treatment status of teacher j in school k, DISTRICT_d is a set of indicators for the six school districts, and W_jk is a vector of teacher background characteristics for teacher j in school k (e.g., the baseline measure of the outcome). _0k represents the average outcome among control teachers in school k, and _1d captures the treatment effect in district d. The overall treatment effect across all six school districts can be computed as a weighted average, with each school district weighted by the number of treatment teachers in the school district. Thus, the overall treatment effect represents the effect of the PD program on a typical treatment teacher in the sample.

For the analyses of treatment effects on teachers classroom practices, we will extend Equation 1 to a two-level hierarchical linear model (HLM) model to explicitly take into account the clustering of lessons observed within teachers. The model will be specified as follows:

Level 1 (lessons):

Y_ijk = π_0jk + ε_ijk (2)

where Y_ijk is the MQI rating of lesson i taught by teacher j in school k, π_0jk is the average rating of the lessons observed for teacher j in school k, and ε_ijk is a random error associated with a given lesson.

Level 2 (teachers):

π_0jk = + + + 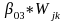r_0jk (3)

The interpretation of Equation 3 is similar to that for Equation 1. In particular, _01d represents the treatment effect on the average lesson rating for individual teachers in district d, and the overall treatment effect can be computed as a weighted average effect across the six school districts.

To test the PD program’s effect on student achievement at the end of the program year (spring 2014), we will construct the following model where students are nested within teachers:

Level 1 (students):

Y_ijk = π_0jk + π_1jk *X_ijk + ε_ijk (4)

where Y_ijk is the test score of student i taught by teacher j in school k, and X_ijk is a vector of demographic characteristics and prior year achievement score of student i taught by teacher j in school k, grand-mean centered. The intercept equation at the school level (Equation 5 below) is identical to Equation 3, with similar interpretations of the terms. The student-level covariate slopes are fixed to their grand means at the school level (Equation 6).

Level 2 (teachers):

π_0jk = + + + 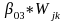r_0jk (5)

π_1jk = (6)

Treatment-on-the-Treated Analyses. It is possible that some teachers assigned to the treatment may not attend the PD activities. Although ITT analyses provide valid estimates of the treatment effects on teachers assigned to the PD program, they may underestimate the treatment effects on teachers who actually attended the PD activities if the number of no shows is not trivial. In that case, we will supplement the ITT analyses with treatment-on-the-treated (TOT) analyses to assess the treatment effects on teachers induced to participate by treatment assignment.

We will conduct the TOT analyses using a standard instrumental variable (IV) approach, where the treatment assignment will serve as the instrument for PD participation (Angrist, Imbens, & Rubin, 1996; Gennetian, Morris, Bos, & Bloom, 2005). During the first stage of the IV analysis, treatment assignment (i.e., IV) is used to obtain the predicted probabilities of PD participation. The predicted values, instead of the original values, of PD participation are then used in the second stage to predict the outcome. The resulting IV estimate of the effect of PD participation can be interpreted as the treatment effect on treatment teachers who were induced to fully participate in the PD program because of treatment assignment (i.e., the local average treatment effect or the treatment effect on compliers).

Dosage Analyses. Given that the level of participation in PD activities (i.e., dosage) is likely to vary across treatment teachers, we will conduct dosage analyses to examine the extent to which the level of PD participation is related to the size of the treatment effect. Our proposed design where teachers are randomly assigned within schools lends itself to a dosage analysis based on the following HLM model, using teacher knowledge as an illustration:

Level 1 (teachers):

Y_jk = _0k + _1k*PD_jk + _2k*W_jk + r_jk (7)

Level 2 (schools):

_0k = + ₀₁*DOSAGE_k + u_0k (8)

_1k = + ₁₁*DOSAGE_k + u_1k (9)

_2k = ₂₀ (10)

In the level 2 model, DOSAGE is a school-level measure of PD participation (e.g., the total number of hours of math PD as part of the study intervention) computed as the average participation level among treatment teachers within a given school.² The parameter of primary interest from this dosage analysis is ₁₁, which indicates the extent to which the treatment effect is larger in schools where the average level of participation among treatment teachers is higher, controlling for whether there is only one or multiple treatment teachers in a school.³ Similar analyses could be conducted to estimate the relationship between dosage and teacher practice or student achievement, using a three-level model.

Analytic Strategy for Analyses of Program Implementation

To describe how the PD intervention was implemented and the challenges associated with implementation (RQ2), we will conduct descriptive analyses of data collected using the measures previously described (with expanded descriptions in the following section). These analyses will describe (1) the extent to which the PD intervention (Intel and MLC) was delivered as intended (fidelity); (2) the proportion of the intended number of hours of the intervention that treatment teachers received (participation); and (3) the difference between PD received by treatment and control teachers (service contrast). Our fidelity of the Intel course and MLC meetings and service contrast analyses will describe the duration, content emphasis, coverage of planned materials, type of learning activities and active engagement of the participants.

We will use the information provided in the teacher surveys to describe the treatment contrast in the number of hours and types of study-relevant PD activities in which teachers participated during the 2013-14 school year. Study-relevant PD activities include extended math content-focused workshops (1/2 day or longer), collaborative meetings that focus on analyzing student work or data (e.g., lesson study) and opportunities for teachers to receive feedback on the quality of their mathematical explanations, through videotaped lessons or direct observations.

Data Collection

IES requests clearance for the study’s data collection instruments, including the teacher knowledge assessment, teacher survey, extant data collection protocol, and study-administered student assessment. Exhibit 7 includes the data collection instruments—the bolded instruments require burden on the part of prospective participants and are the basis of this clearance request.

Exhibit 7. Proposed Data Collection, 2013–2014

Data Source	Number of Records		Collection Schedule
	Treatment	Control	Summer 2013	Fall 2013	Winter 2014	Spring 2014
Teacher knowledge test (N teachers)	100	100	X	X		X
Teacher survey (N teachers)	100	100				X
Video observations for evaluation (N observations)	300	300		X		X
Study administered student test (N students)	1,000	1,000				X
District archival records; approximate N students plus teachers per condition)	2,100	2,100	X			X
Fidelity and log data on PD intervention (Intel, MLC, and Video Feedback)	100	(N/A)	X	X	X	X

Note: Bolded data source items are those that involve burden and for which we request OMB clearance. The number of districts, schools, and teachers for recruitment data collection are estimates projected to obtain the target sample sizes of 6 districts, ~67 schools, and 200 teachers.

Instruments Involving Burden

Parts B.1 (Respondent Universe and Sampling Methods) and B.2 (Procedures for Data Collection) of this package describe the statistical methods and procedures used for screening/recruitment and for the study data collection. Appendix A includes the recruitment materials including the screening protocols described below. Appendix B includes the data collection instruments that carry burden. Brief descriptions of these instruments are provided here.

Screening Protocols. We will use screening protocols at the district, school and teacher levels as the sample is being finalized for the study. The protocols are designed to be as low burden as possible and will take 30 minutes or less for participants to complete. The district screener is designed to confirm that districts are eligible for the study based on size, structure and content of math instruction and competing PD activities or initiatives that may interfere with the study. The school screener will be used to confirm that schools meet study criteria in terms of number of volunteer 4th grade teachers and competing school-based initiatives that may conflict with the study. The teacher screener is designed to confirm interested teachers’ willingness and availability to participate in the study according to study timelines. More details about each of these screeners are included in Part B of this package, and the screeners themselves are included in Appendix A.

Teacher Knowledge Test. Reliable measurement of teacher content knowledge is critical to the proposed study and represents the most proximal outcome of the intervention. We will measure teachers’ content knowledge at baseline (summer 2013), after completion of the Intel course in the fall 2013, and at the end of the school year in June 2014. We will measure teacher content knowledge with a mathematics assessment composed of items in the Massachusetts Test for Educator Licensure (MTEL) for elementary math teachers. We will draw items from the two MTEL assessments: the mathematics subtest of general elementary test (MTEL#03) and the elementary mathematics assessment (MTEL#53). The MTEL assessments were designed and items validated against a set of test objectives developed and reviewed by practicing educators and faculty at educator preparation institutions. Reported reliability for the MTEL is decision consistency in a licensing context (where the most important outcome is the pass/fail decision). The decision consistency for the general elementary test is 0.92 (on a 0 to 1 scale).

We will create three forms of the teacher knowledge test with 30 items selected from the two MTEL math assessments. Items will be selected that align with topics covered in the Intel Math program including foundations and meanings of addition, subtraction, multiplication, and division; connections between and among addition, subtraction, multiplication, and division, operations with fractions, linear relations, and functions. Selected items will cover specific content (such as items that tap the additive inverse or the meaning of fraction multiplication), and items that require making connections among concepts (such as an item that taps both operations with negative numbers and reducing fractions). Each 30-item form of the teacher knowledge test will require no more than 60 minutes to complete and will be pilot tested prior to administration. See Exhibit 8 for the alignment between the topics covered in Intel Math and the item pool from MTEL #03 and MTEL #53. There are one or more items from the MTEL assessments that align with each of the 8 Intel units.

Exhibit 8. Alignment of Intel Math Content and the Teacher Knowledge Item Pool (MTEL)

Content Covered in Intel Math Units	Content Covered in Teacher Knowledge Assessments
	MTEL (#53)	MTEL (#03)
1	5, 12, 42, 44, 50	24, 1
2	1,7	2
3	10, 6, 17	11, 12, 13, 14, 15,17
4	13, 14, 15, 16
5		18
6	9, 19,18, 20, 21, 22, 23, 24,46	3, 6, 7, 8, 9,10, 23,20, 31, 34
7	45,52, 54,57,62, 63,68, 69,72	28, 29, 30
8	11,43

In terms of administration, obtaining a measure of teacher knowledge that is completely exogenous to the study and the PD intervention is a critical aspect of the study. The study team will administer the baseline test in person to all teachers prior to random assignment in summer 2013. This will enable the study to avoid a previously-observed phenomenon known as the “late pretest problem” in which scores on a baseline measure taken after random assignment are affected by treatment status (see Schochet, 2008). The baseline teacher knowledge test will include a couple items at the end that ask teachers about their teaching background.

We will administer the first follow-up measure of teacher knowledge in person in fall 2013 (after the completion of the Intel course), and the second in June 2014. For all three rounds of teacher knowledge test data collection we will follow the procedures we have used in other studies (e.g., The Impact of Two Professional Development Interventions on Early Reading Instruction and Achievement, Garet et al., 2008; Middle School Mathematics Professional Development Impact Study, Garet et al., 2011) to train test proctors and monitor the delivery and the secure transmission of study data. The MTEL items are proprietary and therefore the teacher knowledge instruments are not included in Appendix B.

Teacher Survey. We will administer a spring teacher survey at the same time as the final follow-up teacher knowledge test to all teachers in June 2014. The survey will collect information about teachers’ PD activities from July 2013 – June 2014.  Because we will rely on teacher surveys to provide essential information about teachers’ PD experiences, it will be important to maximize the response rates. The statistical standards of NCES call for response rates of at least 85 percent; we have successfully obtained response rates of 85 percent and higher by offering incentives and creating instruments that are user-friendly, easily understandable, and low burden. The teacher survey is included in this package in Appendix B.

Extant Student Records. The study team will request administrative records for all students who are in the classrooms of the participating teachers at three timepoints: (1) summer/fall 2013 when classroom assignments are formed; (2) in March 2014; and (3) at the time that the spring 2014 state assessment is administered. For all students in participating teachers’ classes at these three points, the study team will request the following data for both the 2012-13 and 2013-14 school years:

• Demographic characteristics (e.g. gender, race/ethnicity)

• English language learner status, special education status, and free- or reduced-price lunch status

• Math achievement scores on the state assessment

The extant data request protocol is included in Appendix B of this package.

Supporting Statement for Paperwork Reduction Act Submission

A. Justification

1. Circumstances Making Collection of Information Necessary

Despite modest gains in recent years, a minority of U.S. students score at or above proficient levels in high-level algebra skills and science on the National Assessment of Educational Progress, and recent math and science achievement scores on the Programme for International Student Assessment consistently place U.S. students in the middle of the pack among the 34 OECD nations (National Center for Education Statistics, 2011; National Mathematics Advisory Panel; 2008; OECD, 2010).

To emphasize how important producing a sizable and highly-skilled Science, Technology, Engineering and Mathematics (STEM) workforce over the next decade is for ensuring sustained U.S. global competitiveness, the current administration has promoted initiatives such as the Educate to Innovate campaign and the inter-agency Committee on STEM, which is developing a targeted five-year strategic plan for federal investments in STEM education. Boosting STEM teacher quality is among the key objectives of these initiatives. There is mounting empirical evidence that teacher quality matters, and not just for student test scores but also for longer-term outcomes such as college attendance, earnings, and retirement savings.

One pathway to improve teacher quality is through in-service training, commonly referred to as

professional development (PD). Significant expenditures are made every year from federal, state,

and local sources to fund teacher PD (upwards of $1.5 billion in 2004-05 for instance). At the

federal level, funding for teacher PD primarily comes from ESEA Title II, which aims to

improve the quality of the teaching workforce.

Although the specific focus of teacher PD varies across federal initiatives, one of the key areas of focus is on teacher preparation to teach math and science, particularly for elementary school teachers who typically teacher multiple subjects. Upper elementary school math courses (grades 4 and 5) typically include topics such as fractions, which are considered critical building blocks for student success in future math courses; however, college-bound high school seniors expecting to enter elementary school education programs as freshmen have math SAT scores well below the national average, many elementary education programs require only a limited amount of math training for its students, and elementary teachers are less likely to have a college or advanced degree in math-related subjects than secondary-level teachers (Greenberg & Walsh, 2008). Thus, despite the substantial expenditures on PD, ostensibly to compensate for this shortfall, many teachers continue to feel unprepared to teach math and science (Epstein and Miller, 2006).

Some mathematicians have argued that any high-quality PD program should include a

comprehensive emphasis on mathematical content knowledge, consistent with the literature

suggesting that having such knowledge is a critical component of being an effective math

teacher (Ball, Thames, & Phelps, 2008; Garet et al., 2011). The U.S. Department of Education (ED) has made a similar argument through its Math Science Partnership (MSP) grant program, which emphasizes summer training institutes for teachers that focus on building mathematical content knowledge. Millions of federal dollars are channeled through the MSP grants to all 50 states each year to meet this goal.

Empirical evidence to support the hypothesized pathway of improving teachers’ content knowledge as a vehicle for improving student outcomes exists, but is limited. Hill, Kapitula, and Umland (2011), for example, reported a correlation of 0.25 between teacher content knowledge as measured by the University of Michigan’s Learning Mathematics for Teaching (LMT) assessment and teacher value-added scores. In another study, Hill, Rowan, and Ball (2005) found that first- and third-grade students gained roughly 0.05 standard deviation (SD) on the Terra Nova math tests for every 1 SD difference in teachers’ LMT scores. Despite limited direct evidence, many mathematicians argue that strengthening teachers’ content knowledge is an important ingredient to improving mathematics teaching and learning.

Another important ingredient of high-quality math PD programs is support for teachers in transferring their newfound content knowledge to the classroom. Teachers’ grasp of the content is manifested in several ways, including, but not limited to, the quality, depth and coherence of their explanations; the precision of their language; the capacity to detect and respond to student errors; and the ability to make use of students’ mathematical reasoning (Hill et al., 2008). Thus, PD programs that seek to improve teachers’ content knowledge should also include a support structure to ensure that the knowledge is transferred and enacted in the classroom. The most recent evidence that these types of classroom practices are associated with improvements in student learning comes from the Measure of Effective Teaching (MET) project (Bill & Melinda Gates Foundation, 2012). Using an abbreviated version of the Mathematical Quality of Instruction (MQI) observation instrument, the MET reported a correlation of 0.12 between the overall scores on the abbreviated MQI instrument and the underlying teacher value-added. In another study, using the complete MQI instrument, Hill et al. (2011) reported a correlation of 0.36.

IES recently released findings from an impact evaluation of math PD that focused on rational numbers concepts for seventh-grade math teachers. The PD focused both on boosting teachers’ knowledge of rational numbers and improving the teaching of rational number concepts. The PD program had some opportunities for teachers to learn pure mathematics content, but not in the way a traditional university mathematics course is structured. After each of the two years of implementation, there were no statistically significant overall impacts on student achievement in rational numbers. The PD program had a significantly positive estimated average effect for one year of the PD program on specialized knowledge of mathematics, based on the pooled year 1 and 2 study samples, for teaching (effect size of 0.28); however, this effect on knowledge did not appear to translate to changes in student achievement. The study also reported small but significant standardized coefficients for the relationships between teachers eliciting student thinking and using representations and student achievement (Garet et al., 2011).

These studies suggest that further examining the impact of teacher PD with (1) a heavy emphasis on developing mathematical content knowledge through the explicit teaching of pure mathematics content, and (2) a well-defined teacher support structure to ensure that the training is transferred into classroom practices, is a critical next step, especially given the lack of rigorous evidence on whether PD that is effective in helping teachers improve student achievement can be delivered at scale (Wayne, Yoon, Zhu, Cronen, & Garet, 2008; Yoon et al., 2011). Recognizing the need, the National Center for Education Evaluation (NCEE) at the Institute of Education Sciences (IES) commissioned a study to evaluate the impact of an intensive, content-focused PD program on teachers’ content knowledge, classroom practice and student achievement. Therefore, this study is designed to rigorously test a PD program that has an intensive and comprehensive mathematical content component and ongoing supports to help teachers incorporate such learning into their everyday teaching. Specifically, the study PD is composed of an intensive 80-hour summer institute for math teachers offered by Intel Math that is 90 percent focused on content knowledge of K-8 math concepts (10 percent on pedagogy). The Intel program is supported by 10 hours of structured professional learning communities that reinforce the implementation of PD practices with a focus on analyzing student work, offered by the Mathematics Learning Community (MLC). The PD program also includes a 3-hour video feedback component in which teachers receive feedback on the quality and clarity of their mathematical explanations on topics addressed in Intel Math and the MLC meetings.

This study will assess impacts of this content-intensive PD on teachers’ content knowledge, classroom practices, and student achievement, thereby contributing evidence to a field in need of high-quality information about improving students’ math performance and teacher quality in our nation’s schools. For these reasons, IES requests clearance to carry out recruitment and data collection activities for the Impact Evaluation of Math Professional Development. More specifically, clearance is requested for the study’s screening protocols used for recruitment, and for the study’s data collection instruments: the teacher knowledge test, teacher survey, district archival records collection protocol, and student assessment.

2. Purposes and Uses of the Data

This request focuses on recruitment and study data collection. Recruitment activities include contacting a sample of districts, schools and teachers to establish their eligibility and interest in participating in the study. Study data include administering three teacher knowledge assessments (summer 2013, fall 2013, June 2014), a teacher survey, a spring 2014 student assessment, and an extant data collection protocol.

Recruitment activities will yield information necessary for the selection of districts and schools to participate. Recruitment data collection includes district screening interviews to ascertain the nature of eligible districts’ current approaches to upper elementary-level math curricula and professional development. We will ask districts about (1) their math curriculum and alignment of it to their state standards and/or Common Core State Standards in Mathematics (CCSSM); (2) the structure of mathematics instruction in their elementary schools (i.e. whether they are departmentalized or have self-contained classes and whether students are sorted into math classes by ability level); and (3) their planned and/or typical PD activities for the evaluation year (summer 2013 – spring 2014). Information from the screening interviews will be used for further in-person discussions with the district and principals and teachers at schools within the district. We will ask an administrator at each school to complete a short questionnaire to confirm that the structure of grade 4 math instruction is aligned with the study (e.g., at least two grade 4 teachers, non-departmentalized math instruction, grade 4 students are not tracked by ability level) and that no major initiatives are planned for the 2013-14 school year that may affect grade 4 math instruction. We will ask the teachers to complete a brief form that confirms their plans to teach grade 4 in the coming year and their interest and availability in participating in the study during summer 2013 and the 2013-14 school year. The teacher form includes a signature line for teachers to confirm their interest in volunteering for the study.

Data collection for the study will yield the information necessary to address the study’s two research questions. The first question asks about the impact of the PD intervention on teacher knowledge, classroom practice, and student achievement. The second question asks about the implementation of the PD intervention and its associated challenges.

3. Use of Technology to Reduce Burden

We plan to make use of technology for both recruitment activities and study data collection.

During recruitment, the district screening interviews will be conducted by phone. For purposes of gathering the information needed to determine district eligibility for the study, telephone interviews have many advantages over mail surveys. First, a telephone interview is less burdensome for respondents, who can provide oral answers. Consequently, a telephone interview is likely to yield a better response rate than a paper survey. Second, telephone interviews can generate responses within minutes once the interviewer reaches the respondent, which helps to maximize the efficiency of our district screening and recruitment process. Third, the interviewer can immediately probe for further information to clarify ambiguous or conditional responses.

In a set of approximately 25 eligible districts, the district screening interviews will be followed up by calls to arrange in-person site visits. We anticipate conducting a first round of in-person visits with district and school staff to further discuss participation in a total of 15 districts, and a second round of visits with a total of eight districts.

The study data collection will also make use of technology. The end-of-year student assessment will be administered online using a Web platform. For the archival data, we will reduce burden by gathering the data electronically rather than in hard copy. We will provide clear instructions regarding the data requested and methods of transmitting the data securely.

A toll-free number and an e-mail address will be available during the data collection process to permit respondents to contact AIR with questions or requests for assistance. The toll-free number and the e-mail address will be included in all communication with respondents.

4. Efforts to Identify Duplication

Before administering the screening protocol, every effort will be made to collect the needed information from archival data on state policy, the Common Core of Data (CCD), district websites, and other knowledgeable sources. These efforts are described in detail under B.1 (Respondent Universe and Sampling Methods) in the subsection, Identifying the Pool of Districts to Be Screened.

Although these sources will help AIR target its efforts, much of the information required to identify eligible districts and schools is either not publicly available or is not kept up-to-date. The screening interviews will therefore allow study staff to collect information not available elsewhere and verify information gathered from public sources.

5. Methods to Minimize Burden on Small Entities

To be considered a small entity by OMB, a school district would need to have a population of fewer than 50,000 students. Our criteria will exclude some of the smallest districts in selecting the district sample. Specifically, as explained further under B.1 (Respondent Universe and Sampling Methods) in the subsection called, Identifying the Pool of Districts to Be Screened, our criteria will require that districts have at least 16 qualifying schools that have at least two eligible teachers in grades 4. These criteria will exclude some of the smallest districts that might be the most burdened by the study requirements.

6. Consequences of Not Collecting the Data

The Impact Evaluation of Math Professional Development represents an ongoing effort by the U.S. Department of Education to rigorously study the effects of in-service training on teachers and students. States and districts are increasingly re-tooling their professional development initiatives, and without this study, states and districts will have a limited understanding of the potential impact of intensively focusing on improving teachers’ content knowledge on math teaching and learning.

With regard to recruitment activities, measuring the impact of the study PD depends on our ability to find districts that meet the study’s criteria with the requisite number of eligible schools and teachers willing to volunteer to participate. If we do not engage in recruitment, the study may be infeasible to conduct or may result in a control condition that is not different enough from the study PD to produce a meaningful treatment-control comparison.

7. Special Circumstances

No special circumstances apply to this study.

8. Federal Register Comments and Persons Consulted Outside the Agency

A 60-day notice was published in the Federal Register, volume 78, no. 8, page 2379 on January 11, 2013, providing an opportunity for public comments. Two comments were received, neither of which was relevant to the collection or substantive enough to require changes.

To assist with the development of the study as a whole, project staff will draw on the experience and expertise of a network of outside experts who will serve as our technical working group (TWG) members. Prospective TWG members must be approved by IES and are still to be determined.

9. Payment or Gifts

The administration of the district-level screening protocol and completion of recruitment activities will involve no payments or gifts. In addition, no incentives will be given to district staff for the collection of district archival records or to students for the collection of the study-administered assessment.

Incentives have been proposed for the teacher knowledge tests and teacher survey to partially offset respondents’ time and effort in completing these instruments. The proposed incentive amounts are based on AIR’s experience conducting two similar evaluations of teacher PD for NCEE: The Impact of Professional Development Strategies on Teacher Practice and Student Achievement in Math and The Impact of Professional Development Models and Strategies on Teacher Practice and Student Achievement in Early Reading. These amounts are within the incentive guidelines outlined in the March 22, 2005, memo, “Guidelines for Incentives for NCEE Evaluation Studies,” prepared for OMB. In particular, we plan to offer a $25 incentive for the spring teacher survey, which is consistent with the incentive guidelines for a 30-minute survey. This memo also stipulates $100 incentives for 1-hour teacher assessments in which there is a high respondent burden. Thus, across the three 1-hour administrations of the teacher knowledge assessment (summer 2013, fall 2013, and June 2014), we plan to offer a $100 incentive per test. The incentive amount for the knowledge test reflects its high burden on respondents- as was the case in previous studies, it is expected to be particularly challenging to obtain respondents for a teacher test, given that it will be 1-hour long, administered 3 times in one year, administered outside of the school day (on the teachers’ own limited time), and will be a knowledge test, which may be perceived as potentially embarrassing or threatening to teachers. In addition, it is important to note that control-group teachers will lack two other potential incentives for participation because they will receive no professional development through the Impact Evaluation of Math Professional Development and will not receive reports of their scores or other feedback.

Incentives are also proposed because high response rates are needed to make the study measures reliable, and we are aware that teachers are the targets of numerous requests to complete data collection instruments on a wide variety of topics from state and district offices, independent researchers, and ED. These requests have been rising in recent years, thus making it increasingly difficult to obtain consistently high response rates. The importance of providing data collection incentives in federal studies has also been described by other researchers (Singer & Kulka, 2004; Berry, Pevar & Zander-Contugno, 2008).

10. Assurances of Confidentiality

No confidential data will be sought during the recruitment phase of the study.

The following statement applies to procedures to take place during the data collection phase of the study. A consistent and cautious approach will be taken to protect all information collected during the data collection phase of the study. This approach will be in accordance with all relevant regulations and requirements. These include the Education Sciences Institute Reform Act of 2002, Title I, Part E, Section 183, which requires “[a]ll collection, maintenance, use, and wide dissemination of data by the Institute … to conform with the requirements of section 552 of Title 5, United States Code, the confidentiality standards of subsections (c) of this section, and sections 444 and 445 of the General Education Provisions Act (20 U.S.C. 1232 g, 1232h).” These citations refer to the Privacy Act, the Family Education Rights and Privacy Act, and the Protection of Pupil Rights Amendment. In addition, for student information, the project director will ensure that all individually identifiable information about students, their academic achievements and families, and information with respect to individual schools shall remain confidential in accordance with section 552a of Title 5, United States Code, the confidentiality standards subsection (c), and sections 444 and 445 of the General Educations Provision Act.

Subsection (c) of Section 183, referenced above, requires the director of IES to “develop and enforce standards designed to protect the confidentiality of persons in the collection, reporting, and publication of data.” The study will also adhere to requirements of subsection (d) of Section 183 prohibiting disclosure of individually identifiable information as well as making the publishing or inappropriate communication of individually identifiable information by employees or staff a felony.

The study team will protect the full privacy and confidentiality of all individuals who provide data. The study will not have data associated with personally identifiable information (PII), as study staff will be assigning random ID numbers to all data records and then stripping any PII from the data records. In addition to the data safeguards described here, the study team will ensure that no respondent names, schools, or districts are identified in publicly available reports or findings, and if necessary, the study team will mask distinguishing characteristics. A statement to this effect will be included with all requests for data:

“American Institutes for Research follow the confidentiality and data protection requirements of IES (The Education Sciences Reform Act of 2002, Title I, Part E, Section 183). Responses to this data collection will be used only for research purposes. The reports prepared for the study will summarize findings across the sample and will not associate responses with a specific district, school, or individual. We will not provide information that identifies respondents to anyone outside the study team, except as required by law.”

The following safeguards are routinely employed by AIR to carry out privacy assurances during the study:

• All AIR employees sign a privacy pledge emphasizing its importance and describing their obligation.

• Identifying information is maintained on separate forms and files, which are linked only by sample identification number.

• Access to hard copy documents is strictly limited. Documents are stored in locked files and cabinets. Discarded materials are shredded.

• Computer data files are protected with passwords and access is limited to specific users.

• Especially sensitive data are maintained on removable storage devices that are kept physically secure when not in use.

11. Justification of Sensitive Questions

No questions of a sensitive nature will be included in the recruitment activities or study data collection instruments.

12. Estimates of Hour Burden

There are two components for which we have calculated hours of burden for this clearance package: recruitment activities, which include the district-level screening and follow-up recruitment activities with districts and school staff, and study data collection, which includes the new (primary) data to be collected for the purpose of the study between summer 2013 and June 2014.

Burden for Recruitment Activities. The total estimated hour burden to complete all recruitment activities is 1,221 hours. This estimate includes district screening, which involves time for district administrators from a pool of 80 districts for a 30-minute initial screener and 45 minutes of follow-up discussions. It also includes time for school administrators and teachers in a progressively smaller number of districts to participate in meetings about the study during two rounds of site visits and to complete school screening and teacher interest forms, and to negotiate final agreements.

On the basis of average hourly wages of participants, the burden of the recruitment efforts amount to $36,785 for all recruitment activities. Exhibit 9 summarizes the estimates of respondent burden for these two study activities.

Exhibit 9. Hour Burden for Respondents for Recruitment Activities

Task	Total Sample Size	Estimated Response Rate	Number of Respondents	Number of Admin-istrations	Number of Responses	Time Estimate (in hours)	Total Hours	Hourly Rate	Estimated Monetary Cost of Burden
District Screening	80	85%	68	1	68	1.25	85	$45	$3,825
School Screening	134	85otentially interested districtsports thespring teacher survey.the target sample sizes of 6 districts, ~67 schools, and 200 teac%	114	1	114	4	456	$35	$15,960
Teacher Screening	400	85%	340	1	340	2	680	$25	$17,000
Total			522		522		1,221		$36,785

Note: The number of districts, schools, and teachers for recruitment data collection are estimates projected to obtain the target sample sizes of 6 districts, ~67 schools, and 200 teachers.

Burden for Study Data Collection. The total estimated hour burden for the data collection is 990 hours. Based on average hourly wages for participants (which were calculated based on estimates of yearly salaries), this amounts to an estimated monetary cost of $28,350. Exhibit 10 summarizes the estimates of respondent burden for the study activities. The burden estimate for the teacher knowledge test includes time for 90 percent of all 200 teachers (treatment and control) in the 6 districts to respond to a 60-minute assessment at three timepoints. The burden estimate for the teacher survey includes time for 90 percent of all 200 teachers (treatment and control) in the 6 districts to respond to a 30-minute survey in June 2014. The district archival records requests require an estimated 20 hours of burden for one district data person to pull the requested data in each district. During the year of the study, we will request that archival records from school years 2012-13 and 2013-14 be provided for students who were in participating teachers’ classrooms at three timepoints: fall 2013, March 2014, and June 2014.

There is no burden associated with any other activities, such as the study-administered student assessment, because all of these measures will be collected by study staff and do not present burden for district or school staff.

Exhibit 10. Hour Burden for Respondents for Study Data Collection

Task	Total Sample Size	Estimated Response Rate	Number of Respondents	Number of Admin-istrations	Number of Responses	Time Estimate (in hours)	Total Hours	Hourly Rate	Estimated Monetary Cost of Burden
Teacher Knowledge Assessment	200	90%	180	3	540	1	540	$25	$13,500
District Archival Records Collection	6	100%	6	3	18	20	360	$35	$12,600
End-of-Year Survey	200	90%	180	1	180	0.5	90	$25	$2,250
Total			366		738		990		$28,350

13. Estimate of Cost Burden to Respondents

There are no additional respondent costs associated with this data collection other than the hour burden accounted for in item 12.

14. Estimate of Annual Cost to the Federal Government

The estimated cost for all aspects of the study is $7,423,166 over 3.5 years, making the annual cost to the federal government $2,120,905.

15. Program Changes or Adjustments

This request is for a new information collection.

16. Plans for Tabulation and Publication of Results

Findings from the Impact Evaluation of Math Professional Development will be reported to IES by AIR in a final study report. We will present findings from analyses conducted to address the two main research questions as described in the Purpose section. The results will be summarized in a study report consistent with NCES reporting standards and accessible to policymakers and research-savvy practitioners. The study report will be accompanied by a nontechnical, stand-alone executive summary. The final report will be disseminated to the public by February 2016.

17. Approval to Not Display OMB Expiration Date

Approval is not being requested; all data collection instruments will include the OMB expiration date.

18. Explanation of Exceptions

No exceptions are requested.

References

Allen, J. P., Pianta, R. C., Gregory, A., Mikami, A.Y., & Lun, J. (2011). An interaction-based approach to enhancing secondary school instruction and student achievement. Science, 333, 1034–1037.

Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching—what makes it special? Journal of Teacher Education. 59(5), 389–407.

Bell, C. A., Wilson, S. M., Higgins, T., & McCoach, D. B. (2010). Measuring the effects of professional development on teacher knowledge: The case of developing mathematical ideas. Journal for Research in Mathematical Education, 41(5), 479–512.

Berry, S. H., Pevar, J. and Zander-Cotugno, M. (2008). Use of Incentives in Surveys Supported by Federal Grants: Paper Presented at Council of Professional Associations on Federal Statistics Seminar Titled "Survey Respondent Incentives: Research and Practice." Santa Monica, CA: RAND Corporation. Retrieved from http://www.rand.org/pubs/working_papers/WR590.

Bill & Melinda Gates Foundation. (2012). Gathering feedback for teaching: Combining high-quality observation with student surveys and achievement gains (MET Project Research Paper). Seattle, WA: Author. Retrieved from http://www.metproject.org/reports.php

Birman, B., LeFloch, K. C., Klekotka, A., Ludwig, M., Taylor, J., Walters, K., et al. (2007). State and local implementation of the No Child Left Behind Act, Volume II—teacher quality under NCLB: Interim report. Washington, DC: U.S. Department of Education.

Carpenter, T. P., Fennema, E., Peterson, P. L., Chiang, C. P., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal 26(4): 499–531.

Epstein, D., & Miller, R. T. (2011). Slow off the mark: Elementary school teachers and the crisis in science, technology, engineering, and math education. Washington, DC: Center for American Progress.

Garet, M, Cronen, S., Eaton, M., Kurki, A., Ludwig, M., Jones, W., et al. (2008). The impact of two professional development interventions on early reading instruction and achievement (NCEE 2008-4030). Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.

Garet, M., Wayne, A., Stancavage, F., Taylor, J., Eaton, M., Walters, K., et al. (2011). Middle school mathematics professional development impact study: Findings after the second year of implementation (NCEE 2011-4024). Washington, DC: National Center for Education Evaluation and Regional Assistance.

Greenberg, J., & Walsh, K. (2008). No common denominator: The preparation of elementary school teachers in mathematics by America’s education schools. Washington, DC: National Council on Teacher Quality.

Hill, H. C., Blunk, M., Charalambous, C., Lewis, J., Phelps, G. C., Sleep, L., et al. (2008). Mathematical knowledge for teaching and the mathematical quality of instruction: An exploratory study. Cognition and Instruction, 26(4), 430–511.

Hill, H. C., Kapitula, L., & Umland, K. (2011). A validity argument approach to evaluating teacher value-added scores. American Educational Research Journal, 48(3), 794–831.

Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371–406.

National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education.

National Science Board. (2012). Science and engineering indicators 2012 (NSB 12-01). Arlington, VA: National Science Foundation.

Raudenbush, S.W. and Sadoff, S. (2008) Statistical Inference When Classroom Quality is Measured With Error. Journal of Research on Educational Effectiveness, 1(2), 138-154.

Schochet, P. (2008). Statistical power for random assignment evaluations of education programs. Journal of Educational Behavioral Statistics, 33(1), 62–87.

Singer, E., and Kulka, R.A. (2004). Paying respondents for survey participation. Studies of Welfare Populations: Data Collection and Research Issues. Retrieved from http://aspe.hhs.gov/hsp/welf-resdata-issues 02/04/04.htm.

Supovitz, J. (2012). The Linking Study—first-year results: A report of the first-year effects of an experimental study of the impact of feedback to teachers on teaching and learning. Paper presented at the annual meeting of the American Educational Research Association, (AERA), Vancouver, BC, Canada.

1 Results from the Measures of Effective Teaching project (Gates Foundation, 2012) indicate that 14 percent of the variance in the scores of lessons rated using MQI is at the teacher, school, and district levels, and 86 percent is due to variation in sections, lessons, and raters (Gates Foundation, 2012, p. 35). For the proposed study, we assumed 86 percent of the total variance in lesson ratings is at the lesson level, 10 percent at the teacher level, and 2 percent each at the school and district levels, which implies that 88 percent of the within-district variance (the basis for effect size) is at the lesson level, 10 percent at the teacher level, and 2 percent at the school level.

2 Because dosage is observed only for treatment teachers, it cannot be used as a teacher-level predictor. Therefore, we use a school-level dosage measure to predict the school-specific treatment effect. Because dosage is measured at the school level, it cannot be used in a model with school fixed effects (there is no variation in school-level dosage within schools); therefore, we treat schools as random effects in this analysis. Before running the fully specified HLM model, we will first estimate the between-school variance of the treatment effect based on a model without any school-level predictors. A meaningful dosage analysis is warranted only if there is significant between-school variation in the treatment effect.

3 A similar model could be estimated with a variable at level 2 indicating whether a school has one or more than one treatment teacher, to test whether the treatment effect is larger if multiple teachers in a school are assigned to participate in the PD program.

File Type	application/vnd.openxmlformats-officedocument.wordprocessingml.document
Author	Kirk Walters
File Modified	0000-00-00
File Created	2021-01-29