HCS_SSB_ATTACH 2_STATISTICAL POWER_SEPTEMBER 2011 FINAL for OMB
HCS_SSB_ATTACH 2_STATISTICAL POWER_SEPTEMBER 2011 FINAL for OMB.docx
The Healthy Communities Study: How Communities Shape Childrens Health (NHLBI)
HCS_SSB_ATTACH 2_STATISTICAL POWER_SEPTEMBER 2011 FINAL for OMB
OMB: 0925-0649
SSB Attachment 2
H
|
|
HEALTHY COMMUNITIES STUDY
ASSESSMENT OF STATISTICAL POWER FOR THE HCS
1. Introduction
The NHLBI Healthy Communities Study seeks to estimate the effectiveness of community programs and policies to reduce childhood obesity. The number of communities included in the study design was chosen to be within the allocated resources available and to allow valid statistical inferences to be made about subtle associations that programs or policies (or their components) have with childhood obesity outcomes over time. The purpose of this analysis is to assess the quality of the proposed study design.
The quality of a study design can be expressed in terms of power and the detectable effect size. Power refers to the probability of correctly rejecting the null hypothesis that the program has zero impact on childhood obesity when the program truly has a non-zero impact. Effect size is the smallest non-zero impact that a program can have on childhood obesity and still be considered statistically different from zero. A study design with high power will tend to reach the correct conclusion about program effectiveness more often than a design with low power. Furthermore, a study design that detects a small effect size is preferable because this design will be able to distinguish subtle levels of program effectiveness from zero effectiveness.
This document describes simulations we conducted to assess the power and effect size of the proposed HCS design. The analysis focused on two outcomes of interest: body mass index (BMI) and a binary measure of physical activity (PA) or nutrition. We assumed that the purpose of the study was to relate the outcomes of interest to a measure of program implementation at the community level. Section 2 describes the statistical models that we used to simulate and analyze the data. Section 3 describes the attributes that we assumed the sampled communities would have, including distributional assumptions about the intensity of program implementation. Section 4 describes the makeup of the study participants in each sampled community. We describe how we generated the BMI data and PA/nutrition data in Sections 5 and 6, respectively. The results of our analysis are provided in Section 7.
2. Statistical Models
We considered several statistical models for each response. For BMI, we considered a fixed-slope longitudinal model that had the following form
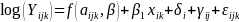(1)
where
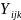is
the kth BMI measurement from child j living
in community i;
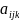is
the age at the time of the BMI measurement;
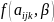is
a polynomial in the child’s age and represents the raw BMI
assuming no community program is implemented;
is
the program intensity level at time k in community i;
is
a random community effect (independent of program implementation);
is
a random child effect independent of the community and age; and
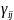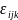is
a random error independent of child and community. The random
effects were drawn from a normal distribution with mean zero and
standard deviations of 0.05 for the community effect (
),
0.19 for the child effect (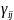
),
and 0.09 for the random error (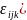
,
with these values established based on prior analyses of longitudinal
BMI data.
We also considered a random-slope longitudinal model for BMI that had the following form:
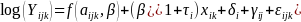(2)
where
each term has the same meaning as Equation (1) and
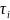is
the random slope effect for community i. The community effect
(
)
was sampled from a normal distribution with zero mean and a standard
deviation of 0.035. To keep the variance comparable across the
fixed-slope and random-slope models, the random slope effect (
)
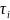was sampled from a normal distribution with zero mean and a standard
deviation equal to 0.035 divided by the square root of the average of
the squared values of
across all BMI records in the simulated dataset. For both
longitudinal BMI models, the same model was used to generate the data
and analyze them.
We considered a cross-sectional fixed-slope BMI model as well. The cross-sectional data were generated using the following equation:
(3)
where
each term has the same meaning as Equation (1) except that the time
subscript, k, is removed. With the time effect removed, the
terms
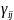and
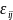both
represent a random error. The model used to fit the cross-sectional
data was therefore
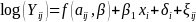(4)
with
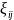representing a random error whose variance is the sum of the variance
for
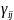and
.
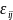For the binary PA/nutrition outcome, we assumed a fixed-slope longitudinal model that had the following form:
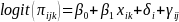(5)
where
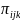is
probability that the binary outcome is present at time k for
child j living in community i;
is
the program intensity level at time k in community i;
is
a random community effect (independent of program implementation);
and
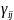is
a random child effect independent of the community and age. The
random effects were drawn from a normal distribution with mean zero
and standard deviations of 0.05 for the community effect (
)
and 0.19 for the child effect (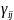
).
These values match those used for the BMI models.
A random-slope longitudinal model was considered for the binary outcome that had the following form:
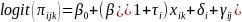(6)
where
each term has the same meaning as Equation (5) and
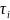is
the random slope effect for community i. For both
longitudinal binary response models, the same model was used to
generate the data and analyze them.
A cross-sectional fixed-slope model was considered for the binary response. The cross-sectional data were generated using the following equation:
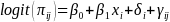(7)
where each term has the same meaning as Equation (6) except that the time subscript, k, is removed from the program intensity level and the response.
For
all statistical models and both outcomes, the hypothesis under
investigation is whether
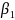equals zero. Effect size is the smallest value of
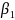that provides a specified power.
3. Modeling Community Attributes
The study design proposes sampling a total of 275 Wave 2 communities. Figure 1 depicts the timing of assessments and medical record abstractions for each year of data collection for the Wave 2 communities. Note that 40 communities are planned to have repeat in-person assessments (RIPA).
Figure
1. Proposed Study Design by Wave 2 Data Collection Year
The central hypothesis under investigation explores the association between community programs or policies (and how they or their component pieces evolve over time) and BMI or PA/nutrition outcomes measured on participant children from within those communities. However, different communities could be implementing programs or policies at different levels of intensity at the time the study is conducted. Based on the study research plan, we assumed that program/policy intensity scores would be measured on a scale between 0 and 1, where 0 means that the program is not implemented at all and 1 means that the program is implemented completely at full intensity.
Since some of the statistical models are longitudinal, we needed to develop a model that explains the change in program intensity over time. Our simulations allowed for the program/policy intensity scores to increase or decrease over time. The following logistic equation was used to simulate how community program/policy intensity scores changes over time:
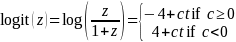
where
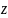is
the program intensity level and
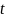is
time in years. The value of c was randomly selected from a
normal distribution with a mean of zero and a standard deviation of
1.25. This distribution allows different simulated communities to
increase or decrease program/policy intensity scores over time at
different rates. The sign of the intercept ensures that two
program/policy intensity score curves with equal but opposite slopes
will reach 0 (for the decreasing program) or 1 (for the increasing
program) after the same number of years.
Each community’s position on the program/policy intensity score curve at the time of the baseline measurement was randomly selected from a beta distribution. The beta family of distributions places a probability on continuous values between 0 and 1. The exact shape of a particular beta distribution is determined by a combination of two parameters, and many different forms are possible that assign more weight to portions of the interval [0, 1]. For purposes of this analysis, we considered three different beta distributions: beta(1, 1), beta(0.5, 2), and beta(1, 2). A beta(1, 1) distribution is equivalent to a uniform distribution that assigns probability equally over the interval [0, 1]. It has a mean of 0.5 and a standard deviation of 0.29. A beta(1, 2) distribution assigns more weight to lower values in the interval, and the weight decreases linearly over the interval. It has a mean of 0.2 and a standard deviation of 0.21. A beta(0.5, 2) distribution is even more heavily weighted towards values in the low end of the interval. It has a mean of 0.33 and a standard deviation of 0.24. Figure 2 depicts the shapes of the three beta distributions used in the analysis.
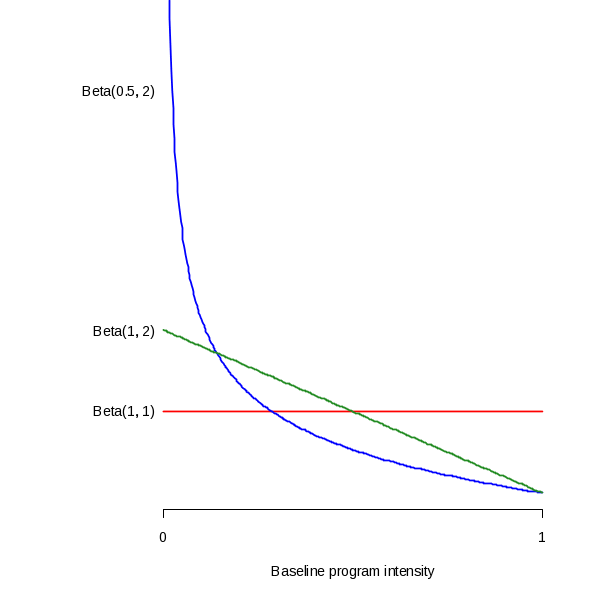
Figure 2. Distributions of Baseline Program Intensity
Figures 3a through 3c illustrate different program/policy intensity score timelines using the three different beta distributions described above. Each figure shows 15 randomly sampled curves, and each of the 15 curves has a different slope and a different initial intensity level. The timeline in each figure starts ten years before the baseline year and ends three years after the baseline year – corresponding to the period of time for which we intend on collecting program/policy information on the RIPA communities. Figure 3a indicates a roughly uniform pattern to the intensity level at the baseline year, as would be expected if the intitial intensity level were sampled from a beta(1, 1) distribution. In Figure 3b, most of the intensity levels at the baseline year are at the lower end of the intensity scale, and even more of the curves are at the lower end of the scale in Figure 3c. These two patterns are to be expected if the intial intensity level were sampled from beta distributions that are skewed to the right. In all three plots, most of the lines have a relatively gradual slope. Furthermore, roughly half of the lines have a positive slope and the other half have a negative slope. These features are to be expected since the slopes were drawn from a normal distribution that is centered at zero.
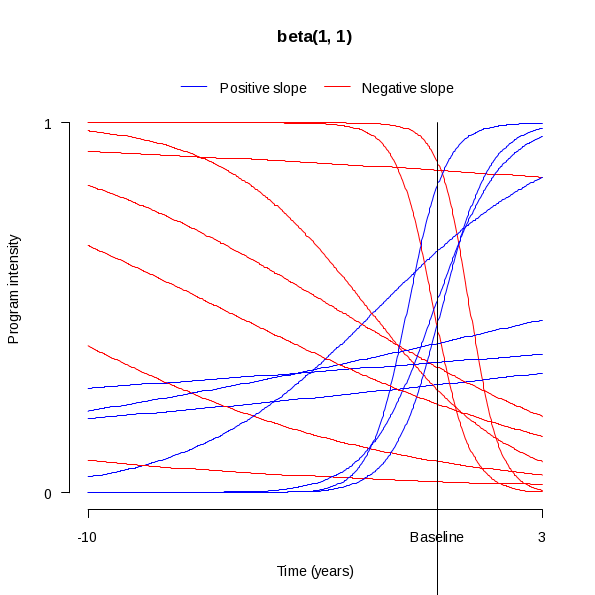
Figure 3a. Sampled Program Timelines Using Beta(1, 1) Distribution for Initial Intensity
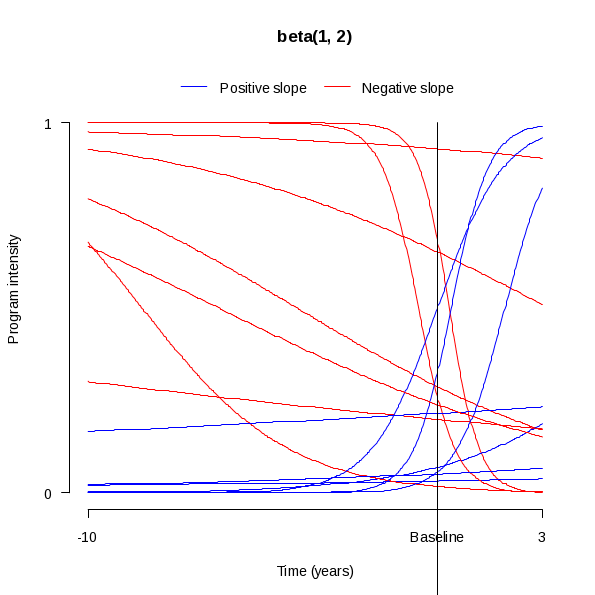
Figure 3b. Sampled Program Timelines Using Beta(1, 2) Distribution for Initial Intensity
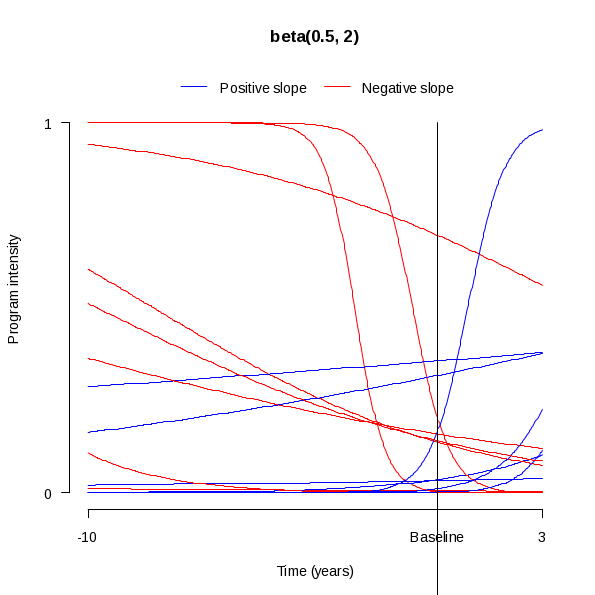
Figure 3c. Sampled Program Timelines Using Beta(0.5, 2) Distribution for Initial Intensity
Once a community’s baseline intensity was simulated, we determined a baseline time on the intensity growth curve for that community. This time was used to determine the relative timing of any additional measurements on the study subjects at times after baseline or before baseline (in the case of medical record abstraction). The relative times were then used to find the community’s intensity level at the time when the additional measurements were taken.
Figure 4 illustrates this concept using BMI measurements from a child in a RIPA community with an increasing program/policy intensity score curve. The baseline intensity level is sampled first, and the curve is used to determine a baseline time that represents how far along the community has progressed in implementing the program. This time is denoted by b in Figure 4. We then calculated the timing of measurement recordings relative to the baseline time using the parameters of the study design and a random process for the timing of medical visits (described in more detail in Section 4). These times were then input into the growth curve formulas to obtain a program/policy intensity score level at the time the measurement was taken. For example, suppose the child represented by Figure 4 was found to have a medical visit 2.1 years before baseline. The value on the growth curve at time (b – 2.1) years would be used to estimate the program/policy intensity score level at the time of the medical visit.
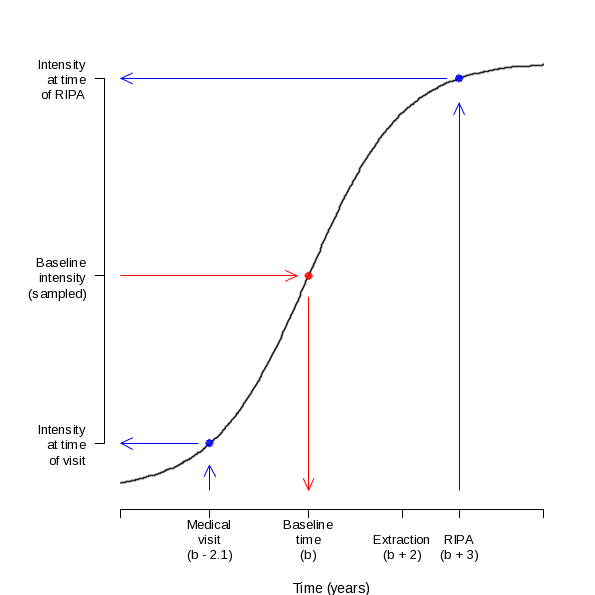
Figure 4. Illustration of Using Growth Curves to Estimate Intensity Score Levels
4. Selecting Community Children
The study design calls for a cohort of 117 children from each RIPA community and 78 children from each non-RIPA community. Within each community, an equal number of children between the ages of 3 and 15 are to be selected for the study. For the RIPA communities, this translates to 9 children at each age level; for non-RIPA communities, there will be 6 children at each age level. The number of males and females at each age level are planned to be equal. (Note that due to an odd number of children being recruited into the RIPA communities within each age group [n=9], gender balance will be maintained across participants in these communities; in half the communities the 9th child for each odd age level [i.e., 3, 5, 7, 9, 11, 13, and 15 year olds] will be female, while the 9th child for each even age level will be male. This pattern will be reversed in the other half of the RIPA communities).
For the simulation, patterned data were made for each community that matches the required number of children at each age level. The exact age of each child at the time of the baseline measurement was equal to the child’s targeted age level plus a randomly selected fraction of a year. For non-RIPA communities, an equal number of simulated subjects were assigned to be male and female. For RIPA communities, each age group consisted of 4 males, 4 females, and one simulated subject who was randomly assigned to be male or female.
The simulation assumed that only 70% of children will participate in follow-up assessments. The children selected for follow-up were randomly selected across all ages and genders within each community.
5. Constructing BMI Data
The simulation assumed that a BMI measurement would be obtained from each child during the baseline assessment. Furthermore, 70% of children in the RIPA communities would have BMI recorded in a follow-up assessment three years after the baseline measurement. Additional BMI measurements would be obtained from medical records for approximately 70% of children in all communities.
We simulated a sequence of medical visits for each child using a non-homogeneous Poisson process. In a Poisson process, the timing of events is determined by an exponential distribution. A non-homogeneous process means that the average number of visits decreases with age. For our simulation, we assumed that the average number of medical visits was two per year up until age 3, one per year from ages 3 to 10, and one every two years after age 10.
Our simulation of medical visits accounted for possible changes in pediatricians. We assumed that, for cost reasons, medical records would be requested from only one pediatrician. Furthermore, we assumed that the pediatrician receiving the request would be the one whom the child visited the most (not necessarily the most recently visited). For each child, we simulated a sequence of changes in pediatrician using a homogeneous Poisson process. The constant mean number of changes was one every 15 years. The simulation allowed for the possibility that some children would have more than one change in physician and that some children would have no change at all.
Once a sequence of visits and changes in physician were simulated, we selected the longest sequence of visits between any changes in physician but before the request for medical records. The result was a sequence of ages when the child’s BMI was measured. Figure 5 depicts the distribution of simulated medical records for ten 15-year olds. The distribution for children younger than age 15 would appear similar, only truncated at the age when the request for medical records was submitted.
Figure 5. Simulated Sequence of Medical Records for Ten 15-Year Olds
Our simulation assumed that only 70% of subjects would have a medical history available. Thus, we randomly selected 30% of children from each community and disregarded their simulated medical visits. The time that the request for medical records was fulfilled was sampled from a uniform distribution ranging from 3 to 6 months after the baseline visit.
The simulated medical history along with the timing of the study’s in-person assessments provided a sequence of ages at which the subject’s BMI was measured. We used these ages, and the child’s gender to determine a raw BMI from CDC’s 2000 BMI-for-age percentiles (http://www.cdc.gov/growthcharts/html_charts/bmiagerev.htm). The raw BMI is the BMI that the child would have if there were no community programs implemented.
Each
child’s measured BMI was simulated using the statistical models
in Section 2. In that model,
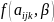represents the raw BMI following the median BMI in the CDC tables.
The community’s program intensity level,
,
was determined from the intensity growth curves (illustrated in
Figure 4). The random child effect (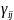
)
captures any child-specific deviation from the median BMI in the CDC
tables.
6. Constructing Binary Outcomes
Our simulation of binary outcomes was more straightforward than our simulation of BMI measurements since the former does not rely on a history of medical visits. Each child was assumed to receive a baseline assessment. We then assumed that 70% of the children in each community would have a follow-up assessment, the timing and number of which were simulated exactly as specified in the proposed study design. For children in the RIPA communities, follow-up assessments occurred two years and three years after the baseline assessment. For children in the first wave of non-RIPA communities, a single follow-up assessment occurred two years after the baseline assessment. For children in the second wave of communities, a single follow-up assessment occurred one year after the baseline assessment. Children in the third wave of communities did not receive any follow-up assessment.
The
binary outcome was sampled from a Bernoulli distribution. The
probability of a success was determined by the statistical model
described in Section 2. The community’s program intensity
level,
,
was determined from the intensity growth curves (illustrated in
Figure 4).
The
value of
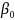was calculated such that the prevalence of the outcome was equal to
0.5. The prevalence is equal to the unconditional probability of the
outcome and involves integrating over the distribution of the
values. Since three different beta distributions were used for the
intensity levels, the simulation used three different values of
:
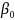-0.475 for the beta(1, 1) distribution, -0.189 for the beta(0.5, 2)
distribution, and -0.316 for the beta(1, 2) distribution.
7. Results
Using
the methods described above, we replicated study data 500 times for
each baseline intensity distribution depicted in Figure 2. For each
replication, we fit the appropriate statistical model to the
simulated data. We recorded the point estimate of
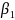and
the standard error of the estimate for each model fit. Taking the
average of the 500 standard error estimates of
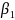provided us with an estimate of the true standard error of
.
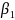Using
our estimate of the standard error of
,
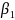we can calculate the combinations of power and effect size attainable
from the study design. For a two-sided test, the effect size is
determined from the following equation:
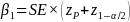
where
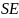is
the standard error estimated from the simulation,
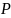is
the power,
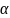is
the significance level of the test, and
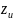is
the 100*uth percentile from a standard
normal distribution.
After the data are collected, a researcher may be interested in analyzing the effectiveness of a program that targets a particular age group. There are at least two possible ways of doing this type of analysis given the proposed design. One approach would use all data that were measured when a subject’s age was within the age group of interest regardless of the subject’s age at the baseline assessment, allowing analyses of how community programs/policies (and how they change over time) influence child obesity outcomes within specific age groups. For example, suppose a subject who was 15 years old at the baseline assessment was found to have medical records containing BMI information when she was 4 years old. Those records could be included in an analysis focusing on the 3-4 year-old age group. A second approach would use all data ever measured on an individual whose baseline age fell within the age group of interest, enabling specific cohort analyses. For example, a study focusing on 3-4 year-olds would include all data collected on those children that were ages 3 or 4 at the baseline assessment. Our simulation study addressed both of these research approaches.
Table 1 lists the effect size as a percentage change in BMI that could be detected for a one-unit change in program intensity, assuming a fixed-slope longitudinal model. Results are listed for selected powers and significance levels. Effect sizes were estimated for the different beta distributions used to sample baseline program intensities and for the different approaches for treating age-specific studies. Table 2 provides equivalent information for the binary response. Tables 3 and 4 provide similar information for cross-sectional analyses of the data collected at baseline. Tables 5 and 6 provide results for the random-slope longitudinal models for BMI and the binary outcome, respectively.
The results of the power analysis in Table 1 show that longitudinal analysis will be able to detect very subtle associations between BMI outcomes (from the combined in-person assessments and medical record reviews) and community program/policy intensity scores – with the study being well powered to detect BMI changes of <1% attributable to the 1-unit change in community program/policy intensity score across all age-groups combined, and changes of <3% across most specific age groups.
The results provided in Table 2 demonstrate reasonably subtle associations can be detected based on longitudinal analyses of binary physical activity or nutritional outcomes from the Stage-1 assessment tool (collected at in-person assessments and planned remote follow-ups) – with the study being well powered to detect changes of 3-4% in these PA/nutritional outcomes attributable to the 1-unit change in community program/policy intensity score across all age-groups combined, and changes of 6-10% across most specific age groups.
The results provided in Table 3 demonstrate that the study will be able to detect less-subtle associations between community program/policy intensity scores and BMI outcomes measured at baseline (using cross-sectional analyses), with the study being well powered to detect BMI changes of 3 - 4.5% attributable to the 1-unit change in community program/policy intensity score across all age-groups combined, and changes of 4 - 8% across most specific age groups.
Similarly, results provided in Table 4 demonstrate that the study will be able to detect less-subtle associations between community program/policy intensity scores and the binary physical activity and/or nutritional outcomes measured at baseline (using cross-sectional analyses), with the study being well powered to detect changes of 4 - 6% attributable to the 1-unit change in community program/policy intensity score across all age-groups combined, and changes of 8 - 12% across most specific age groups.
When a random-slope effect is added to the BMI longitudinal model, the study design is less able to detect subtle effects sizes than when the slope is assumed to be fixed, as shown in the Table 5. If we assume that each community will have a particular slope associated with program/policy intensity score, the study is well powered to detect BMI changes that are slightly larger than those when the slope is assumed to be fixed across all communities – still allowing for the detection of some fairly subtle relationships.
Table 6 indicates that the performance of the study design with respect to the binary outcome does not change when a random-slope effect is added to the model.
Lastly, it should be noted that these results are sensitive to a number of assumptions related to the availability of data, participation rates, the anticipated distribution(s) of how community program/policy index scores change over time, etc. Further study could be conducted to assess the sensitivity of these results to these assumptions.
Table 1. Power and Effect Size Results for BMI Response
Power |
Alpha |
Age group |
Effect Size (% change in BMI that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
Age group refers to age when measurement recorded |
|||||
0.8 |
0.05 |
All ages |
0.37% |
0.39% |
0.39% |
3-4 |
0.76% |
0.83% |
0.78% |
||
5-6 |
0.92% |
0.99% |
0.95% |
||
7-8 |
0.98% |
1.07% |
1.01% |
||
9-10 |
1.07% |
1.21% |
1.11% |
||
11-13 |
0.74% |
0.87% |
0.78% |
||
14-15 |
2.70% |
3.28% |
3% |
||
0.9 |
0.05 |
All ages |
0.43% |
0.46% |
0.46% |
3-4 |
0.88% |
0.96% |
0.91% |
||
5-6 |
1.06% |
1.14% |
1.09% |
||
7-8 |
1.13% |
1.23% |
1.17% |
||
9-10 |
1.23% |
1.40% |
1.29% |
||
11-13 |
0.86% |
1.01% |
0.90% |
||
14-15 |
3.13% |
3.80% |
3.48% |
||
0.9 |
0.01 |
All ages |
0.51% |
0.54% |
0.54% |
3-4 |
1.05% |
1.14% |
1.08% |
||
5-6 |
1.26% |
1.36% |
1.30% |
||
7-8 |
1.35% |
1.47% |
1.39% |
||
9-10 |
1.47% |
1.67% |
1.53% |
||
11-13 |
1.02% |
1.20% |
1.07% |
||
14-15 |
3.74% |
4.54% |
4.15% |
||
Age group refers to age at baseline |
|||||
0.8 |
0.05 |
All ages |
0.26% |
0.27% |
0.28% |
3-4 |
0.31% |
0.36% |
0.33% |
||
5-6 |
0.39% |
0.42% |
0.42% |
||
7-8 |
0.54% |
0.57% |
0.58% |
||
9-10 |
0.69% |
0.71% |
0.74% |
||
11-13 |
0.64% |
0.65% |
0.68% |
||
14-15 |
0.78% |
0.79% |
0.83% |
||
0.9 |
0.05 |
All ages |
0.30% |
0.32% |
0.32% |
3-4 |
0.36% |
0.42% |
0.39% |
||
5-6 |
0.45% |
0.49% |
0.48% |
||
7-8 |
0.62% |
0.66% |
0.67% |
||
9-10 |
0.80% |
0.82% |
0.86% |
||
11-13 |
0.74% |
0.75% |
0.79% |
||
14-15 |
0.90% |
0.92% |
0.97% |
||
0.9 |
0.01 |
All ages |
0.36% |
0.38% |
0.39% |
3-4 |
0.43% |
0.50% |
0.46% |
||
5-6 |
0.53% |
0.59% |
0.58% |
||
7-8 |
0.74% |
0.78% |
0.80% |
||
9-10 |
0.95% |
0.98% |
1.02% |
||
11-13 |
0.88% |
0.89% |
0.94% |
||
14-15 |
1.07% |
1.09% |
1.15% |
||
Table 2. Power and Effect Size Results for Binary Response
Power |
Alpha |
Age group |
Effect Size (% Change in a Binary Physical Activity or Nutritional Outcome that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
Age group refers to age when measurement recorded |
|||||
0.8 |
0.05 |
All ages |
2.47% |
3.16% |
2.83% |
3-4 |
7.72% |
10.13% |
9.51% |
||
5-6 |
6.09% |
7.87% |
7.03% |
||
7-8 |
5.90% |
7.55% |
6.72% |
||
9-10 |
5.90% |
7.55% |
6.72% |
||
11-13 |
4.83% |
6.19% |
5.50% |
||
14-15 |
5.88% |
7.55% |
6.71% |
||
0.9 |
0.05 |
All ages |
2.85% |
3.66% |
3.27% |
3-4 |
8.91% |
11.67% |
10.95% |
||
5-6 |
7.04% |
9.08% |
8.11% |
||
7-8 |
6.81% |
8.71% |
7.76% |
||
9-10 |
6.81% |
8.71% |
7.76% |
||
11-13 |
5.59% |
7.15% |
6.36% |
||
14-15 |
6.80% |
8.72% |
7.74% |
||
0.9 |
0.01 |
All ages |
3.39% |
4.35% |
3.89% |
3-4 |
10.56% |
13.78% |
12.95% |
||
5-6 |
8.35% |
10.75% |
9.62% |
||
7-8 |
8.09% |
10.32% |
9.20% |
||
9-10 |
8.09% |
10.33% |
9.20% |
||
11-13 |
6.64% |
8.49% |
7.55% |
||
14-15 |
8.07% |
10.33% |
9.18% |
||
Age group refers to age at baseline |
|||||
0.8 |
0.05 |
All ages |
2.38% |
3.04% |
2.70% |
3-4 |
5.91% |
7.58% |
6.73% |
||
5-6 |
5.91% |
7.57% |
6.74% |
||
7-8 |
5.91% |
7.58% |
6.74% |
||
9-10 |
5.91% |
7.57% |
6.74% |
||
11-13 |
4.84% |
6.21% |
5.52% |
||
14-15 |
5.90% |
7.57% |
6.72% |
||
0.9 |
0.05 |
All ages |
2.75% |
3.51% |
3.13% |
3-4 |
6.82% |
8.74% |
7.77% |
||
5-6 |
6.83% |
8.73% |
7.78% |
||
7-8 |
6.83% |
8.75% |
7.78% |
||
9-10 |
6.83% |
8.73% |
7.78% |
||
11-13 |
5.59% |
7.17% |
6.38% |
||
14-15 |
6.82% |
8.74% |
7.76% |
||
0.9 |
0.01 |
All ages |
3.27% |
4.18% |
3.72% |
3-4 |
8.10% |
10.36% |
9.21% |
||
5-6 |
8.10% |
10.35% |
9.23% |
||
7-8 |
8.10% |
10.37% |
9.22% |
||
9-10 |
8.11% |
10.35% |
9.22% |
||
11-13 |
6.64% |
8.51% |
7.57% |
||
14-15 |
8.09% |
10.36% |
9.21% |
||
Table 3. Cross-Sectional Power and Effect Size Results for BMI Response
Power |
Alpha |
Age group |
Effect Size (% change in BMI that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
0.8 |
0.05 |
All ages |
3.23% |
4.27% |
3.89% |
3-4 |
4.38% |
5.84% |
5.26% |
||
5-6 |
4.42% |
5.88% |
5.32% |
||
7-8 |
4.42% |
5.86% |
5.31% |
||
9-10 |
4.42% |
5.88% |
5.30% |
||
11-13 |
4.01% |
5.34% |
4.79% |
||
14-15 |
4.32% |
5.73% |
5.19% |
||
0.9 |
0.05 |
All ages |
3.75% |
4.96% |
4.51% |
3-4 |
5.09% |
6.78% |
6.11% |
||
5-6 |
5.13% |
6.83% |
6.18% |
||
7-8 |
5.13% |
6.81% |
6.17% |
||
9-10 |
5.13% |
6.84% |
6.16% |
||
11-13 |
4.65% |
6.20% |
5.57% |
||
14-15 |
5.02% |
6.66% |
6.03% |
||
0.9 |
0.01 |
All ages |
4.48% |
5.93% |
5.39% |
3-4 |
6.08% |
8.12% |
7.31% |
||
5-6 |
6.14% |
8.18% |
7.40% |
||
7-8 |
6.14% |
8.16% |
7.38% |
||
9-10 |
6.14% |
8.19% |
7.37% |
||
11-13 |
5.56% |
7.42% |
6.66% |
||
14-15 |
6% |
7.98% |
7.22% |
||
Table 4. Cross-Sectional Power and Effect Size Results for Binary Response
Power |
Alpha |
Age group |
Effect Size (% Change in a Binary Physical Activity or Nutritional Outcome that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
0.8 |
0.05 |
All ages |
3.36% |
4.46% |
4% |
3-4 |
8.40% |
11.06% |
9.95% |
||
5-6 |
8.38% |
11.03% |
9.95% |
||
7-8 |
8.38% |
11.07% |
9.95% |
||
9-10 |
8.39% |
11.05% |
9.97% |
||
11-13 |
6.88% |
9.09% |
8.17% |
||
14-15 |
8.38% |
11.08% |
9.94% |
||
0.9 |
0.05 |
All ages |
3.89% |
5.15% |
4.63% |
3-4 |
9.69% |
12.72% |
11.46% |
||
5-6 |
9.67% |
12.70% |
11.46% |
||
7-8 |
9.67% |
12.74% |
11.46% |
||
9-10 |
9.68% |
12.72% |
11.49% |
||
11-13 |
7.94% |
10.48% |
9.43% |
||
14-15 |
9.67% |
12.75% |
11.45% |
||
0.9 |
0.01 |
All ages |
4.62% |
6.12% |
5.50% |
3-4 |
11.47% |
15.01% |
13.54% |
||
5-6 |
11.45% |
14.97% |
13.54% |
||
7-8 |
11.44% |
15.03% |
13.54% |
||
9-10 |
11.45% |
15% |
13.57% |
||
11-13 |
9.42% |
12.39% |
11.16% |
||
14-15 |
11.45% |
15.04% |
13.52% |
||
Table 5. Power and Effect Size Results for BMI Response, Random Slope
Power |
Alpha |
Age group |
Effect Size (% change in BMI that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
Age group refers to age when measurement recorded |
|||||
0.8 |
0.05 |
All ages |
1.24% |
1.62% |
1.37% |
3-4 |
1.46% |
1.85% |
1.60% |
||
5-6 |
1.69% |
2.08% |
1.84% |
||
7-8 |
1.76% |
2.18% |
1.92% |
||
9-10 |
1.82% |
2.28% |
1.97% |
||
11-13 |
1.48% |
1.96% |
1.62% |
||
14-15 |
3.57% |
4.79% |
4.16% |
||
0.9 |
0.05 |
All ages |
1.44% |
1.88% |
1.58% |
3-4 |
1.69% |
2.14% |
1.86% |
||
5-6 |
1.96% |
2.41% |
2.13% |
||
7-8 |
2.04% |
2.52% |
2.22% |
||
9-10 |
2.11% |
2.64% |
2.28% |
||
11-13 |
1.72% |
2.27% |
1.88% |
||
14-15 |
4.14% |
5.57% |
4.83% |
||
0.9 |
0.01 |
All ages |
1.72% |
2.24% |
1.89% |
3-4 |
2.02% |
2.55% |
2.21% |
||
5-6 |
2.33% |
2.87% |
2.54% |
||
7-8 |
2.44% |
3.01% |
2.65% |
||
9-10 |
2.52% |
3.15% |
2.72% |
||
11-13 |
2.05% |
2.71% |
2.24% |
||
14-15 |
4.95% |
6.66% |
5.77% |
||
Age group refers to age at baseline |
|||||
0.8 |
0.05 |
All ages |
1.22% |
1.59% |
1.35% |
3-4 |
1.16% |
1.56% |
1.28% |
||
5-6 |
1.31% |
1.69% |
1.43% |
||
7-8 |
1.75% |
2.11% |
1.90% |
||
9-10 |
2.08% |
2.40% |
2.23% |
||
11-13 |
1.78% |
2.11% |
1.92% |
||
14-15 |
1.67% |
2.01% |
1.80% |
||
0.9 |
0.05 |
All ages |
1.41% |
1.85% |
1.56% |
3-4 |
1.35% |
1.81% |
1.48% |
||
5-6 |
1.52% |
1.96% |
1.65% |
||
7-8 |
2.03% |
2.45% |
2.20% |
||
9-10 |
2.41% |
2.79% |
2.59% |
||
11-13 |
2.06% |
2.44% |
2.22% |
||
14-15 |
1.94% |
2.33% |
2.09% |
||
0.9 |
0.01 |
All ages |
1.68% |
2.20% |
1.86% |
3-4 |
1.60% |
2.16% |
1.76% |
||
5-6 |
1.81% |
2.33% |
1.97% |
||
7-8 |
2.42% |
2.92% |
2.62% |
||
9-10 |
2.88% |
3.32% |
3.09% |
||
11-13 |
2.46% |
2.92% |
2.65% |
||
14-15 |
2.31% |
2.78% |
2.49% |
||
Table 6. Power and Effect Size Results for Binary Response, Random Slope
Power |
Alpha |
Age group |
Effect Size (% Change in a Binary Physical Activity or Nutritional Outcome that can be detected) |
||
beta(1, 1) Uniform |
beta(0.5, 2) Curved Decline |
beta(1, 2) Linear Decline |
|||
Age group refers to age when measurement recorded |
|||||
0.8 |
0.05 |
All ages |
2.45% |
3.05% |
2.79% |
3-4 |
7.80% |
10.42% |
9.46% |
||
5-6 |
6.11% |
7.61% |
6.97% |
||
7-8 |
5.93% |
7.29% |
6.69% |
||
9-10 |
5.91% |
7.32% |
6.67% |
||
11-13 |
4.84% |
5.97% |
5.46% |
||
14-15 |
5.90% |
7.27% |
6.67% |
||
0.9 |
0.05 |
All ages |
2.83% |
3.53% |
3.23% |
3-4 |
9.00% |
12.00% |
10.90% |
||
5-6 |
7.05% |
8.78% |
8.04% |
||
7-8 |
6.85% |
8.41% |
7.73% |
||
9-10 |
6.83% |
8.45% |
7.70% |
||
11-13 |
5.59% |
6.89% |
6.31% |
||
14-15 |
6.81% |
8.39% |
7.70% |
||
0.9 |
0.01 |
All ages |
3.37% |
4.20% |
3.84% |
3-4 |
10.66% |
14.16% |
12.89% |
||
5-6 |
8.37% |
10.41% |
9.53% |
||
7-8 |
8.13% |
9.97% |
9.17% |
||
9-10 |
8.11% |
10.01% |
9.13% |
||
11-13 |
6.64% |
8.18% |
7.50% |
||
14-15 |
8.09% |
9.95% |
9.13% |
||
Age group refers to age at baseline |
|||||
0.8 |
0.05 |
All ages |
2.36% |
2.92% |
2.67% |
3-4 |
5.91% |
7.32% |
6.70% |
||
5-6 |
5.92% |
7.32% |
6.71% |
||
7-8 |
5.93% |
7.33% |
6.71% |
||
9-10 |
5.91% |
7.32% |
6.70% |
||
11-13 |
4.85% |
5.98% |
5.47% |
||
14-15 |
5.91% |
7.29% |
6.69% |
||
0.9 |
0.05 |
All ages |
2.73% |
3.38% |
3.09% |
3-4 |
6.83% |
8.44% |
7.74% |
||
5-6 |
6.84% |
8.45% |
7.74% |
||
7-8 |
6.85% |
8.46% |
7.74% |
||
9-10 |
6.83% |
8.45% |
7.73% |
||
11-13 |
5.60% |
6.90% |
6.32% |
||
14-15 |
6.83% |
8.42% |
7.72% |
||
0.9 |
0.01 |
All ages |
3.24% |
4.01% |
3.67% |
3-4 |
8.11% |
10.01% |
9.18% |
||
5-6 |
8.12% |
10.01% |
9.18% |
||
7-8 |
8.13% |
10.02% |
9.18% |
||
9-10 |
8.11% |
10.02% |
9.17% |
||
11-13 |
6.66% |
8.19% |
7.50% |
||
14-15 |
8.11% |
9.98% |
9.16% |
||
| File Type | application/vnd.openxmlformats-officedocument.wordprocessingml.document |
| Author | Chris Sroka |
| File Modified | 0000-00-00 |
| File Created | 2021-01-31 |
© 2024 OMB.report | Privacy Policy